الگوریتم جستجوی اول سطح چیست؟ پیمایش سطحی (BFS) چیست؟

الگوریتم جستجوی اول سطح (BFS) برای جستجو در ساختمان دادهآموزش ساختمان داده و الگوریتمهر ساختمان داده یک نوع فرمت ذخیره‌سازی و مدیریت داده‌ها در کامپیوتر است، که امکان دسترسی و اصلاح کارآمد آن داده‌ها را برای یکسری از الگوریتم‌ها و کاربردها فراهم می‌کند، در این صفحه به بررسی و آموزش ساختمان داده و الگوریتم پرداخته شده است درخت یا گرافگراف چیست، آموزش گراف از 0 تا 100 توسط دانشجو ارشد صنعتی شریفدر این مقاله تمامی مطالب مربوط به گراف از 0 تا 100 تدریس شده است. مواردی همچون : گراف چیست؟ انواع گراف، گراف همبند، مکمل گراف،‌ گراف کامل، گراف جهت دار، گراف بدون جهت،‌ گراف ساده و ...، برای پیدا کردن گره هدف استفاده می‌شود. این الگوریتمالگوریتم چیست به زبان ساده و با مثال های فراواندر این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد از ریشه درخت یا گراف شروع گرده و قبل از رفتن به گره‌ها در عمق بعدی، همه گره‌ها را در عمق فعلی جستجو یا بازدید می‌کند. جستجوی اول سطح می‌تواند برای حل بسیاری از مسائل در نظریه گرافهمه چیز در مورد نظریه گراف (Graph Theory)در این مقاله یک مقدمه جامع در رابطه با نظریه گراف ارائه شده است و سعی شده نشان داده شود که دانستن برخی از مبانی نظریه گراف تا چه میزان می‌تواند مفید و موثر باشد. استفاده شود. در این مقاله ما به معرفی و بررسی این الگوریتم می‌پردازیم.

الگوریتم جستجوی اول سطح

الگوریتم جستجوی اول سطح، تمام گره‌های گراف را در دو دسته قرار می‌دهد.

گره‌های ویزیت شده (Visited)
گره‌های ویزیت نشده (Not Visited)

هدف این الگوریتم این است که تمام گره‌ها را در دسته ویزیت شده قرار دهد. نحوه کارکرد این الگوریتم به صورت زیر است:

گره شروع را در صف قرار می‌دهیم.
گره اول صف را برمی‌داریم و آن را در دسته ویزیت شده قرار می‌دهیم.
تمام گره‌هایی که همسایه گره ویزیت شده هستند و هنوز ویزیت نشده‌اند را در آخر صف قرار می‌دهیم.
مراحل 2 و 3 را تا زمانی که صف خالی شود، تکرار می‌کنیم.

حتما بخوانید :

معرفی انواع الگوریتم‌ ها

مثال الگوریتم جستجوی اول سطح

حال با یک مثال نحوه کارکرد الگوریتم جستجوی اول سطح یا BFS را بررسی می‌کنیم.

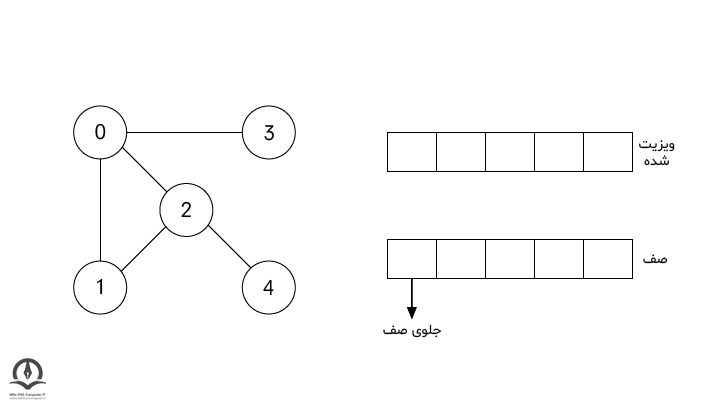
با گره 0 شروع می‌کنیم. الگوریتم، این گره را در دسته گره‌های ویزیت شده قرار می‌دهد و تمام گره‌های همسایه آن ‌که گره‌های 1، 2 و 3 هستند را به صف منتقل می‌کند.

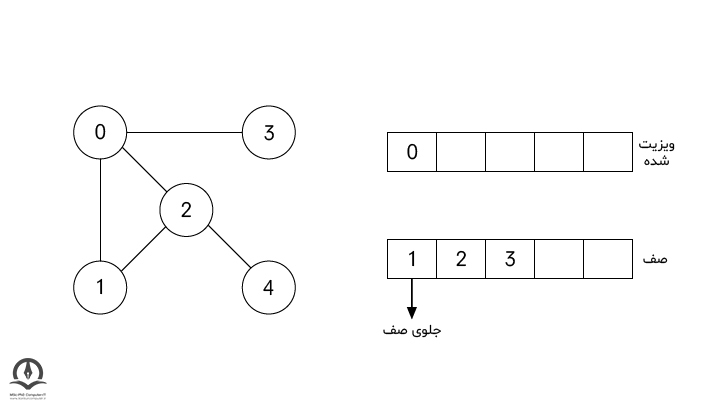
در این مرحله، الگوریتم، اولین گره صف که در مثال ما گره 1 است را ویزیت کرده و به دسته ویزیت شده منتقل می‌کند. تمام همسایه‌های گره 1 در صف هستند، گره‌ای به صف اضافه نمی‌شود.

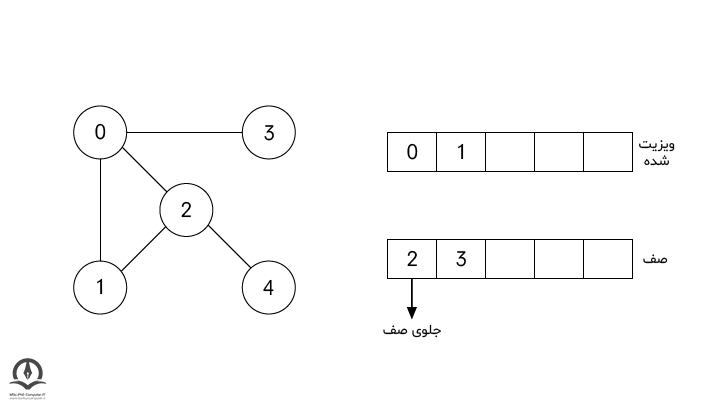
در مرحله بعدی، الگوریتم گره 2 را که در جلوی صف قرار دارد ویزیت کرده و به دسته ویزیت‌ شده‌ها منتقل می‌کند و تنها گره همسایه آن که در صف قرار ندارد، یعنی گره 4 را به صف اضافه می‌کند.

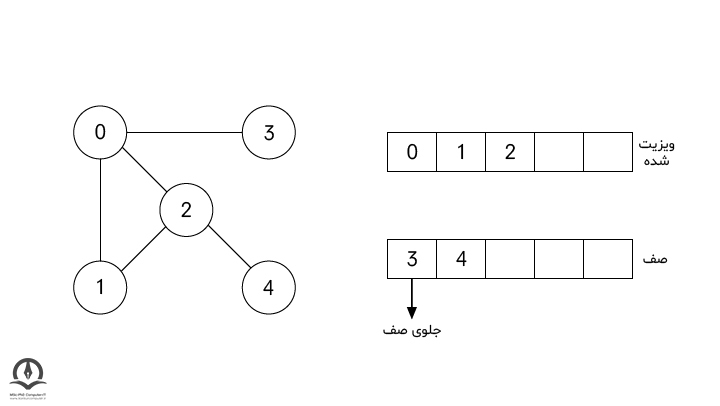
در مرحله بعد، الگوریتم گره 3 را که در ابتدای صف قرار دارد را ویزیت می‌کند و به دسته ویزیت‌ شده‌ها منتقل می‌کند.

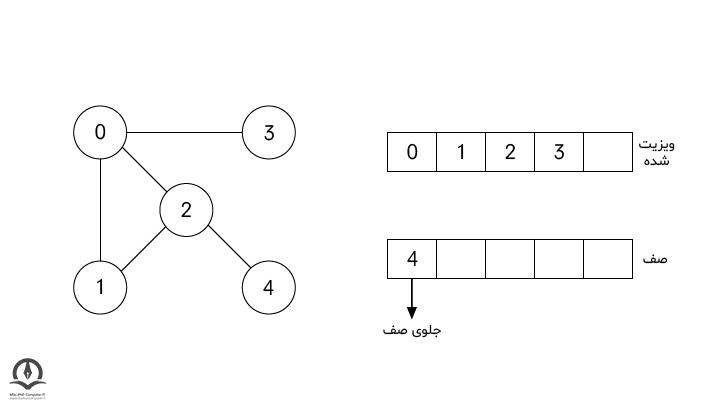
در نهایت، الگوریتم گره 4 را ویزیت می‌کند؛ چون پس از این مرحله صف خالی می‌شود، الگوریتم جستجوی اول سطح پس از این مرحله به پایان می‌رسد.

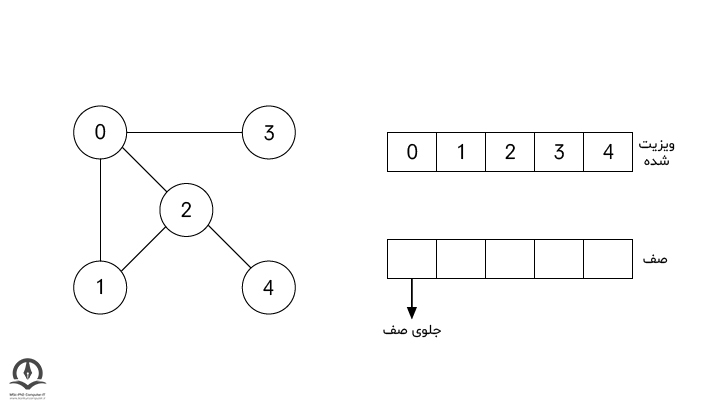
پیاده‌سازی الگوریتم جستجوی اول سطح

Pseudo Code

شبه کد الگوریتم BFS در زیر نشان داده شده است:

create a queue Q 
mark v as visited and put v into Q 
while Q is non-empty 
  remove the head u of Q 
  mark and enqueue all (unvisited) neighbours of u

create a queue Q 
mark v as visited and put v into Q 
while Q is non-empty 
  remove the head u of Q 
  mark and enqueue all (unvisited) neighbours of u

در بخش بعدی پیاده‌سازی الگوریتم BFS با چهار زبان برنامه نویسیزبان های برنامه نویسی چیست؟این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده محبوب آورده شده است. کدهای زیر در نهایت سادگی پیاده‌سازی شده‌اند تا بتوانیم تمرکز اصلی را روی خود الگوریتم جستجوی اول سطح بگذاریم.

حتما بخوانید :

الگوریتم knn ⚡️ الگوریتم K نزدیک ترین همسایه

Python

# BFS algorithm in Python

import collections

# BFS algorithm
def bfs(graph, root):

  visited, queue = set(), collections.deque([root])
  visited.add(root)

  while queue:

    # Dequeue a vertex from queue
    vertex = queue.popleft()
    print(str(vertex) + " ", end="")

    # If not visited, mark it as visited, and
    # enqueue it
    for neighbour in graph[vertex]:
      if neighbour not in visited:
        visited.add(neighbour)
        queue.append(neighbour)

if __name__ == '__main__':
  graph = {0: [1, 2], 1: [2], 2: [3], 3: [1, 2]}
  print("Following is Breadth First Traversal: ")
  bfs(graph, 0)

# BFS algorithm in Python

import collections

# BFS algorithm
def bfs(graph, root):

  visited, queue = set(), collections.deque([root])
  visited.add(root)

  while queue:

    # Dequeue a vertex from queue
    vertex = queue.popleft()
    print(str(vertex) + " ", end="")

    # If not visited, mark it as visited, and
    # enqueue it
    for neighbour in graph[vertex]:
      if neighbour not in visited:
        visited.add(neighbour)
        queue.append(neighbour)


if __name__ == '__main__':
  graph = {0: [1, 2], 1: [2], 2: [3], 3: [1, 2]}
  print("Following is Breadth First Traversal: ")
  bfs(graph, 0)

Java

// BFS algorithm in Java

import java.util.*;

public class Graph {
  private int V;
  private LinkedList<Integer>adj[];

  // Create a graph
  Graph(int v) {
    V = v;
    adj = new LinkedList[v];
    for (int i = 0; i  v; ++i)
      adj[i] = new LinkedList();
  }

  // Add edges to the graph
  void addEdge(int v, int w) {
    adj[v].add(w);
  }

  // BFS algorithm
  void BFS(int s) {

    boolean visited[] = new boolean[V];

    LinkedList<Integer> queue = new LinkedList();

    visited[s] = true;
    queue.add(s);

    while (queue.size() != 0) {
      s = queue.poll();
      System.out.print(s + " ");

      Iterator<Integer> i = adj[s].listIterator();
      while (i.hasNext()) {
        int n = i.next();
        if (!visited[n]) {
          visited[n] = true;
          queue.add(n);
        }
      }
    }
  }

  public static void main(String args[]) {
    Graph g = new Graph(4);

    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    System.out.println("Following is Breadth First Traversal " + "(starting from vertex 2)");

    g.BFS(2);
  }
}

// BFS algorithm in Java

import java.util.*;

public class Graph {
  private int V;
  private LinkedList<Integer>adj[];

  // Create a graph
  Graph(int v) {
    V = v;
    adj = new LinkedList[v];
    for (int i = 0; i  v; ++i)
      adj[i] = new LinkedList();
  }

  // Add edges to the graph
  void addEdge(int v, int w) {
    adj[v].add(w);
  }

  // BFS algorithm
  void BFS(int s) {

    boolean visited[] = new boolean[V];

    LinkedList<Integer> queue = new LinkedList();

    visited[s] = true;
    queue.add(s);

    while (queue.size() != 0) {
      s = queue.poll();
      System.out.print(s + " ");

      Iterator<Integer> i = adj[s].listIterator();
      while (i.hasNext()) {
        int n = i.next();
        if (!visited[n]) {
          visited[n] = true;
          queue.add(n);
        }
      }
    }
  }

  public static void main(String args[]) {
    Graph g = new Graph(4);

    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    System.out.println("Following is Breadth First Traversal " + "(starting from vertex 2)");

    g.BFS(2);
  }
}

C

// BFS algorithm in C

#include <stdio.h>
#include <stdlib.h>
#define SIZE 40

struct queue {
  int items[SIZE];
  int front;
  int rear;
};

struct queue* createQueue();
void enqueue(struct queue* q, int);
int dequeue(struct queue* q);
void display(struct queue* q);
int isEmpty(struct queue* q);
void printQueue(struct queue* q);

struct node {
  int vertex;
  struct node* next;
};

struct node* createNode(int);

struct Graph {
  int numVertices;
  struct node** adjLists;
  int* visited;
};

// BFS algorithm
void bfs(struct Graph* graph, int startVertex) {
  struct queue* q = createQueue();

  graph->visited[startVertex] = 1;
  enqueue(q, startVertex);

  while (!isEmpty(q)) {
    printQueue(q);
    int currentVertex = dequeue(q);
    printf(“Visited %d\n”, currentVertex);

    struct node* temp = graph->adjLists[currentVertex];

    while (temp) {
      int adjVertex = temp->vertex;

      if (graph->visited[adjVertex] == 0) {
        graph->visited[adjVertex] = 1;
        enqueue(q, adjVertex);
      }
      temp = temp->next;
    }
  }
}

// Creating a node
struct node* createNode(int v) {
  struct node* newNode = malloc(sizeof(struct node));
  newNode->vertex = v;
  newNode->next = NULL;
  return newNode;
}

// Creating a graph
struct Graph* createGraph(int vertices) {
  struct Graph* graph = malloc(sizeof(struct Graph));
  graph->numVertices = vertices;

  graph->adjLists = malloc(vertices * sizeof(struct node*));
  graph->visited = malloc(vertices * sizeof(int));

  int I;
  for (i = 0; i adjLists[i] = NULL;
    graph->visited[i] = 0;
  }

  return graph;
}

// Add edge
void addEdge(struct Graph* graph, int src, int dest) {
  // Add edge from src to dest
  struct node* newNode = createNode(dest);
  newNode->next = graph->adjLists[src];
  graph->adjLists[src] = newNode;

  // Add edge from dest to src
  newNode = createNode(src);
  newNode->next = graph->adjLists[dest];
  graph->adjLists[dest] = newNode;
}

// Create a queue
struct queue* createQueue() {
  struct queue* q = malloc(sizeof(struct queue));
  q->front = -1;
  q->rear = -1;
  return q;
}

// Check if the queue is empty
int isEmpty(struct queue* q) {
  if (q->rear == -1)
    return 1;
  else
    return 0;
}

// Adding elements into queue
void enqueue(struct queue* q, int value) {
  if (q->rear == SIZE – 1)
    printf(“\nQueue is Full!!”);
  else {
    if (q->front == -1)
      q->front = 0;
    q->rear++;
    q->items[q->rear] = value;
  }
}

// Removing elements from queue
int dequeue(struct queue* q) {
  int item;
  if (isEmpty(q)) {
    printf(“Queue is empty”);
    item = -1;
  }
  else {
    item = q->items[q->front];
    q->front++;
    if (q->front > q->rear)
    {
      printf(“Resetting queue “);
      q->front = q->rear = -1;
    }
  }
  return item;
}

// Print the queue
void printQueue(struct queue* q) {
  int I = q->front;

  if (isEmpty(q)) {
    printf(“Queue is empty”);
  }
  else {
    printf(“\nQueue contains \n”);
    for (i = q->front; i items[i]);
    }
  }
}

int main() {
  struct Graph* graph = createGraph(6);
  addEdge(graph, 0, 1);
  addEdge(graph, 0, 2);
  addEdge(graph, 1, 2);
  addEdge(graph, 1, 4);
  addEdge(graph, 1, 3);
  addEdge(graph, 2, 4);
  addEdge(graph, 3, 4);

  bfs(graph, 0);

  return 0;
}

// BFS algorithm in C

#include <stdio.h>
#include <stdlib.h>
#define SIZE 40

struct queue {
  int items[SIZE];
  int front;
  int rear;
};

struct queue* createQueue();
void enqueue(struct queue* q, int);
int dequeue(struct queue* q);
void display(struct queue* q);
int isEmpty(struct queue* q);
void printQueue(struct queue* q);

struct node {
  int vertex;
  struct node* next;
};

struct node* createNode(int);

struct Graph {
  int numVertices;
  struct node** adjLists;
  int* visited;
};

// BFS algorithm
void bfs(struct Graph* graph, int startVertex) {
  struct queue* q = createQueue();

  graph->visited[startVertex] = 1;
  enqueue(q, startVertex);

  while (!isEmpty(q)) {
    printQueue(q);
    int currentVertex = dequeue(q);
    printf(“Visited %d\n”, currentVertex);

    struct node* temp = graph->adjLists[currentVertex];

    while (temp) {
      int adjVertex = temp->vertex;

      if (graph->visited[adjVertex] == 0) {
        graph->visited[adjVertex] = 1;
        enqueue(q, adjVertex);
      }
      temp = temp->next;
    }
  }
}

// Creating a node
struct node* createNode(int v) {
  struct node* newNode = malloc(sizeof(struct node));
  newNode->vertex = v;
  newNode->next = NULL;
  return newNode;
}

// Creating a graph
struct Graph* createGraph(int vertices) {
  struct Graph* graph = malloc(sizeof(struct Graph));
  graph->numVertices = vertices;

  graph->adjLists = malloc(vertices * sizeof(struct node*));
  graph->visited = malloc(vertices * sizeof(int));

  int I;
  for (i = 0; i adjLists[i] = NULL;
    graph->visited[i] = 0;
  }

  return graph;
}

// Add edge
void addEdge(struct Graph* graph, int src, int dest) {
  // Add edge from src to dest
  struct node* newNode = createNode(dest);
  newNode->next = graph->adjLists[src];
  graph->adjLists[src] = newNode;

  // Add edge from dest to src
  newNode = createNode(src);
  newNode->next = graph->adjLists[dest];
  graph->adjLists[dest] = newNode;
}

// Create a queue
struct queue* createQueue() {
  struct queue* q = malloc(sizeof(struct queue));
  q->front = -1;
  q->rear = -1;
  return q;
}

// Check if the queue is empty
int isEmpty(struct queue* q) {
  if (q->rear == -1)
    return 1;
  else
    return 0;
}

// Adding elements into queue
void enqueue(struct queue* q, int value) {
  if (q->rear == SIZE – 1)
    printf(“\nQueue is Full!!”);
  else {
    if (q->front == -1)
      q->front = 0;
    q->rear++;
    q->items[q->rear] = value;
  }
}

// Removing elements from queue
int dequeue(struct queue* q) {
  int item;
  if (isEmpty(q)) {
    printf(“Queue is empty”);
    item = -1;
  }
  else {
    item = q->items[q->front];
    q->front++;
    if (q->front > q->rear)
    {
      printf(“Resetting queue “);
      q->front = q->rear = -1;
    }
  }
  return item;
}

// Print the queue
void printQueue(struct queue* q) {
  int I = q->front;

  if (isEmpty(q)) {
    printf(“Queue is empty”);
  }
  else {
    printf(“\nQueue contains \n”);
    for (i = q->front; i items[i]);
    }
  }
}

int main() {
  struct Graph* graph = createGraph(6);
  addEdge(graph, 0, 1);
  addEdge(graph, 0, 2);
  addEdge(graph, 1, 2);
  addEdge(graph, 1, 4);
  addEdge(graph, 1, 3);
  addEdge(graph, 2, 4);
  addEdge(graph, 3, 4);

  bfs(graph, 0);

  return 0;
}

C++

// BFS algorithm in C++

#include <iostream>
#include <list>

using namespace std;

class Graph {
  int numVertices;
  list<int>* adjLists;
  bool* visited;

  public:
  Graph(int vertices);
  void addEdge(int src, int dest);
  void BFS(int startVertex);
};

// Create a graph with given vertices,
// and maintain an adjacency list
Graph::Graph(int vertices) {
  numVertices = vertices;
  adjLists = new list<int>[vertices];
}

// Add edges to the graph
void Graph::addEdge(int src, int dest) {
  adjLists[src].push_back(dest);
  adjLists[dest].push_back(src);
}

// BFS algorithm
void Graph::BFS(int startVertex) {
  visited = new bool[numVertices];
  for (int i = 0; i < numVertices; i++)
    visited[i] = false;

  list<int> queue;

  visited[startVertex] = true;
  queue.push_back(startVertex);

  list ::iterator I;

  while (!queue.empty()) {
    int currVertex = queue.front();
    cout  “Visited “  currVertex  “ “;
    queue.pop_front();

    for (I = adjLists[currVertex].begin(); I != adjLists[currVertex].end(); ++i) {
      int adjVertex = *I;
      if (!visited[adjVertex]) {
        visited[adjVertex] = true;
        queue.push_back(adjVertex);
      }
    }
  }
}

int main() {
  Graph g(4);
  g.addEdge(0, 1);
  g.addEdge(0, 2);
  g.addEdge(1, 2);
  g.addEdge(2, 0);
  g.addEdge(2, 3);
  g.addEdge(3, 3);

  g.BFS(2);

  return 0;
}

// BFS algorithm in C++

#include <iostream>
#include <list>

using namespace std;

class Graph {
  int numVertices;
  list<int>* adjLists;
  bool* visited;

  public:
  Graph(int vertices);
  void addEdge(int src, int dest);
  void BFS(int startVertex);
};

// Create a graph with given vertices,
// and maintain an adjacency list
Graph::Graph(int vertices) {
  numVertices = vertices;
  adjLists = new list<int>[vertices];
}

// Add edges to the graph
void Graph::addEdge(int src, int dest) {
  adjLists[src].push_back(dest);
  adjLists[dest].push_back(src);
}

// BFS algorithm
void Graph::BFS(int startVertex) {
  visited = new bool[numVertices];
  for (int i = 0; i < numVertices; i++)
    visited[i] = false;

  list<int> queue;

  visited[startVertex] = true;
  queue.push_back(startVertex);

  list ::iterator I;

  while (!queue.empty()) {
    int currVertex = queue.front();
    cout  “Visited “  currVertex  “ “;
    queue.pop_front();

    for (I = adjLists[currVertex].begin(); I != adjLists[currVertex].end(); ++i) {
      int adjVertex = *I;
      if (!visited[adjVertex]) {
        visited[adjVertex] = true;
        queue.push_back(adjVertex);
      }
    }
  }
}

int main() {
  Graph g(4);
  g.addEdge(0, 1);
  g.addEdge(0, 2);
  g.addEdge(1, 2);
  g.addEdge(2, 0);
  g.addEdge(2, 3);
  g.addEdge(3, 3);

  g.BFS(2);

  return 0;
}

پیچیدگی زمانی و فضایی الگوریتم جستجوی اول سطح

از آن‌جایی که در بدترین حالت، جستجوی اول سطح باید همه مسیرها را به تمام گره‌های ممکن در نظر بگیرد، پیچیدگی زمانی جستجوی اول سطح برابر با $\mathrm{O}\left(\left|\mathrm{E}\right|\mathrm{+}\left|\mathrm{V}\right|\right)$ است که در آن $\left|\mathrm{V}\right|$ و $\left|\mathrm{E}\right|$ کاردینالیته یا تعداد اعضای مجموعه رئوس و یال‌ها به ترتیب است. همچنین، از آن‌جایی که همه گره‌های یک سطح باید ذخیره شوند تا زمانی که گره‌های فرزندشان در سطح بعدی تولید شوند، پیچیدگی فضایی متناسب با تعداد گره‌ها در عمیق‌ترین سطح است. پیچیدگی فضایی را می‌توان به صورت $\mathrm{O}\left(\left|\mathrm{V}\right|\right)$ نیز بیان کرد که در آن $\left|\mathrm{V}\right|$ کاردینالیته مجموعه رئوس است. در بدترین حالت، گراف عمق 1 دارد و تمام رئوس باید ذخیره شوند.

حتما بخوانید :

پیچیدگی زمانی الگوریتم چیست؟ معرفی نماد های مجانبی

کاربردهای الگوریتم جستجوی اول سطح

کوتاه ترین مسیر و درخت پوشای کمینه برای گراف بدون وزن: در گراف بدون وزن، کوتاه‌ترین مسیر، مسیری است که کمترین تعداد یال را دارد. با جستجوی اول سطح، ما همیشه از یک رأس مبدأ با استفاده از حداقل تعداد یال‌ها به رأس مقصد می‌رسیم؛ همچنین، در مورد گراف‌های بدون وزن، هر درخت پوشا یک درخت پوشای کمینه است و می‌توانیم از پیمایش اول عمق یا عرض برای یافتن درخت پوشا استفاده کنیم.
درخت پوشای کمینه برای گراف های وزن دار: همچنین می‌توانیم درخت پوشای کمینه را برای گراف‌های وزن‌دار با استفاده از BFS پیدا کنیم، اما شرط این است که وزن یال‌ها باید غیرمنفی و برای هر جفت رئوس یکسان باشد.
شبکه های همتا به همتا: در شبکه های همتا به همتا مانند BitTorren و Breadth First Search برای یافتن تمام گره‌های همسایه استفاده می‌شود.
خزنده ها (Crawlers) در موتورهای جستجو: خزنده‌ها با استفاده از Breadth First Search یک فهرست می‌سازند. ایده آن به این صورت است که از صفحه مبدأ شروع کنید و همه پیوندها را از مبدأ دنبال کنید و همین کار را ادامه دهید. DFSالگوریتم جستجوی اول عمق ⚡️ آموزش الگوریتم dfs گرافدر این مقاله عالی الگوریتم جستجوی اول عمق بررسی و الگوریتم dfs گراف آموزش داده شده و مثال ها و پیاده سازی و کاربردهای الگوریتم جستجوی اول (DFS) عمق بیان شده هم می‌تواند برای خزنده‌ها استفاده شود، اما مزیت Breadth First Search این است که عمق یا سطوح درخت ساخته شده را می‌توان محدود کرد.
شبکه های اجتماعی: در شبکه‌های اجتماعی، می‌توانیم افرادی را در فاصله k از یک شخص با استفاده از جستجوی اول سطح تا سطوح k پیدا کنیم.
سیستم های GPS: جستجوی اول سطح برای یافتن تمام مکان‌های همسایه استفاده می‌شود.
پخش در شبکه: در شبکه‌ها، یک بسته پخش شده از جستجوی اول سطح استفاده می‌کند تا به همه گره‌ها برسد.
تشخیص دور در گراف بدون جهت: در گراف‌های بدون جهت، می‌توان از جستجوی اول سطح یا جستجوی اول عمق برای تشخیص دور استفاده کرد. ما می‌توانیم از BFS برای تشخیص دور در یک گراف جهت‌دار نیز استفاده کنیم.
الگوریتم فورد – فالکرسون: در الگوریتم فورد-فالکرسون، می‌توانیم از پیمایش اول سطح یا پیمایش اول عمق برای یافتن حداکثر جریان استفاده کنیم. در این الگوریتم پیمایش اول سطح ترجیح داده می‌شود زیرا پیچیدگی زمانی را در بدترین حالت به $\mathrm{O}\left(\mathrm{V}{\mathrm{E}}^{\mathrm{2}}\right)$ کاهش می‌دهد.
تشخیص دوبخشی بودن یک گراف: برای تشخیص دوبخشی بودن یک گراف می‌توانیم از پیمایش اول سطح یا پیمایش اول عمق استفاده کنیم.
مسیریابی: می‌توانیم از پیمایش اول سطح یا پیمایش اول عمق استفاده کنیم تا ببینیم آیا مسیری بین دو رأس وجود دارد یا خیر.
یافتن همه گره ها در یک مؤلفه متصل گراف: می‌توانیم از پیمایش اول سطح یا پیمایش اول عمق برای یافتن تمام گره‌های موجود در یک مولفه متصل گراف استفاده کنیم.
هوش مصنوعی: در هوش مصنوعیهوش مصنوعی (AI) چیست؟ انواع، کاربردها، مزایا و معایبهوش مصنوعی یا Artificial Intelligence یا به اختصار AI، امروزه کاربردهای بسیاری پیدا کرده و به یکی از داغ‌ترین حوزه‌های بشر تبدیل شده است، اما با این وجود بسیاری از افراد با کاربردهای آن آشنایی کامل ندارند، به همین علت در این صفحه کاربردها، مزایا و معایب AI بطور کامل بررسی شده است، BFS در پیمایش درخت بازی برای یافتن بهترین حرکت استفاده می‌شود.
امنیت شبکه: در زمینه امنیت شبکه، از BFS در عبور از یک شبکه برای یافتن تمامی دستگاه‌های متصل به آن استفاده می‌شود.
مرتب سازی توپولوژیکی: از BFS می‌توان برای یافتن ترتیب توپولوژیکی گره‌ها در یک گراف بدون دور جهت‌دار (DAG) استفاده کرد.
پردازش تصویر: از BFS می‌توان در بحث پردازش تصویرپردازش تصویر دیجیتال چیست؟ چه انواعی دارد؟ چه مراحلی را شامل می‌شود؟ پردازش تصویر یکی از فیلدهای پرطرفدار مرتبط با گرافیک کامپیوتر، بینایی کامپیوتر، هوش مصنوعی، یادگیری ماشین، و الگوریتم‌ها و محاسبات است که ارتباط تنگاتنگی میان تمام آنهاست. در نتیجه در این صفحه علاوه بر معرفی این فیلد، نقشه راهی نیز برای علاقه‌مندان این حوزه ارائه کرده‌ایم. برای پر کردن تصویر با رنگی خاص یا یافتن اجزای متصل پیکسل‌ها استفاده کرد.
سیستم‌های توصیه گر (Recommender Systems): BFS می‌تواند برای یافتن آیتم‌های مشابه در یک مجموعه داده بزرگ با پیمایش اتصالات آیتم‌ها در یک گراف شباهت دار استفاده شود.

مزایای جستجوی اول سطح

جستجوی اول سطح مزایای بسیاری دارد که از بین آنها می‌توان به موارد زیر اشاره کرد:

BFS هرگز در حلقهحلقه در برنامه نویسی چیست؟ حلقه یا لوپ (Loop) چیست؟این مقاله عالی به زبان ساده و با استفاده از فیلم توضیح داده که حلقه در برنامه نویسی چیست، همچنین در خصوص حلقه یا لوپ (Loop) بی نهایت صحبت کرده است دور بی‌نهایت گرفتار نمی‌شود.
اگر راه‌حلی برای مسئله وجود داشته باشد، BFS آن را پیدا خواهد کرد.
اگر بیش از یک راه‌حل وجود داشته باشد، BFS می‌تواند حداقل راه‌حلی را که به تعداد مراحل کمتری نیاز دارد، بیابد.
به‌راحتی قابل پیاده‌سازی است.

حتما بخوانید :

الگوریتم پریم (Prim) چیست ⚡️مثال+پیاده سازی+پیچیدگی زمانی

معایب جستجوی اول سطح

اشکال اصلی BFS نیاز آن به حافظهحافظه در کامپیوتر، همه چیز در مورد حافظه در معماری کامپیوتردر این مقاله به بررسی کامل حافظه در کامپیوتر، انواع حافظه در کامپیوتر، کش، روش‌های آدرس دهی کش، نگاشت آدرس و موارد دیگر می‌پردازیم است. از آن‌جایی که هر سطح از نمودار باید ذخیره شود تا سطح بعدی تولید شود و مقدار حافظه متناسب با تعداد گره‌های ذخیره شده است، پیچیدگی فضایی جستجوی اول سطح از مرتبه $\mathrm{O}\left(\mathrm{bd}\right)$ است، که b ضریب انشعاب است (تعداد فرزندان در هر گره) و d عمق است. در نتیجه، BFS در عمل به شدت محدود به فضا است، بنابراین حافظه موجود در رایانه‌های معمولی را در عرض چند دقیقه تمام می‌کند.

جمع‌بندی

الگوریتم جستجوی اول سطح ابزار قدرتمند برای حل بسیاری از انواع مختلف مسائل است. BFS یک الگوریتم کارآمد است که می‌تواند برای پیمایش یک گراف و یافتن کوتاه‌ترین مسیر بین دو گره استفاده شود؛ همچنین برای یافتن کوتاه‌ترین مسیر بین دو نقطه در یک مسئله ماز هم مفید است. جستجوی اول سطح یک ابزار مهم برای بسیاری از حوزه‌ها از جمله هوش مصنوعی، بازی ها و روباتیک است. با مزایای بسیاری که دارد، جای تعجب نیست که چرا الگوریتم جستجوی اول سطح، یک انتخاب محبوب برای بسیاری از انواع مختلف مشکلات است.

الگوریتم جستجوی اول سطح (Breadth First Search) یا BFS چیست؟

الگوریتم Breadth First Search (BFS) یک گراف را به‌صورت سطحی پیمایش می‌کند و از یک صف برای به خاطر سپردن رأس بعدی برای ادامه جستجو استفاده می‌کند، زمانی که یک بن‌بست در هر تکرار رخ می‌دهد.

DFS بهتر است یا BFS؟

BFS زمانی بهتر کار می‌کند که کاربر رئوسی را جستجو می‌کند که به مبدأ نزدیک‌تر هستند. زمانی که کاربر بخواهد راه‌حل‌ها را جدای از هر مبدأ مشخصی پیدا کند، DFS بهتر کار می‌کند.

کاربردهای BFS چیست؟

BFS در سیستم‌های GPS برای یافتن مکان‌های همسایه استفاده می‌شود. در شبکه، زمانی که می‌خواهیم چند بسته را پخش کنیم، از الگوریتم BFS استفاده می‌کنیم. الگوریتم مسیریابی بر اساس BFS یا DFS است. BFS در الگوریتم فورد-فولکرسون برای یافتن حداکثر جریان در یک شبکه استفاده می‌شود.

در پیاده سازی الگوریتم BFS از چه ساختمان داده ای استفاده می‌شود؟

در پیاده‌سازی‌های استاندارد ،BFS از ساختمان داده صف استفاده می‌شود.

محدودیت های الگوریتم BFS چیست؟

الگوریتم Breadth First Search چند عیب را دارد: این الگوریتم می‌تواند حافظه زیادی را اشغال کند، زیرا باید تمام گره‌های درخت جستجو را پیمایش کند. می‌تواند کند باشد زیرا همه گره‌ها را در هر سطح قبل از رفتن به سطح بعدی گسترش می‌دهد.