الگوریتم پریم یک الگوریتم درخت پوشای کمینه است که یک گراف وزن‌دار را به‌عنوان ورودی می‌گیرد و زیرمجموعه یالهای گراف آن را به‌گونه‌ای پیدا میکند که:
- درختی را تشکیل دهد که شامل هر رأس است.
- دارای حداقل مجموع وزن‌ها در بین تمام درختانی است که می‌توان از گراف تشکیل داد.
در این آموزش نحوه عملکرد الگوریتم پریم را خواهید آموخت؛ همچنین نمونه‌های کارکردی از الگوریتم پریم را در پایتون، جاوا، C و سی پلاس پلاس خواهید دید.
الگوریتم پریم
این الگوریتم در دسته‌ای از الگوریتم‌ها به‌نام الگوریتم‌های حریصانه قرار می‌گیرد که بهینه محلی را به امید یافتن یک بهینه جهانی پیدا می‌کنند. در الگوریتم پریم از یال‌هایی با کمترین وزن شروع می‌کنیم و به اضافه کردن یالها ادامه می‌دهیم تا به هدف خود برسیم.
مراحل پیاده سازی الگوریتم پریم به‌شرح زیر است:
- درخت اولیه را با یک راس به‌طور تصادفی ایجاد می‌کنیم.
- تمام یال‌هایی را که درخت را به رئوس جدید متصل میکند، پیدا می‌کنیم، حداقل را پیدا می‌کنیم و آن را به درخت اضافه می‌کنیم.
- به تکرار مرحله 2 ادامه می‌دهیم تا زمانی که درخت پوشای کمینه را بدست آوریم.
مثالی از الگوریتم پریم
گراف وزن‌دار زیر را در نظر بگیرید:
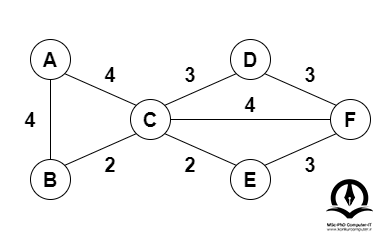
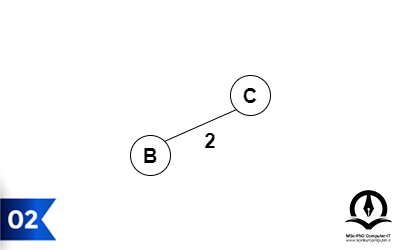
می‌خواهیم درخت پوشای کمینه این گراف را به‌دست آوریم (توجه کنید درخت پوشای کمینه در یک گراف لزوما یکتا نیست). یکی از رئوس گراف را برای شروع انتخاب می‌کنیم (در اینجا راس B را انتخاب کردیم).
یال با کمترین وزن از این راس را انتخاب و به درخت اضافه می‌کنیم.
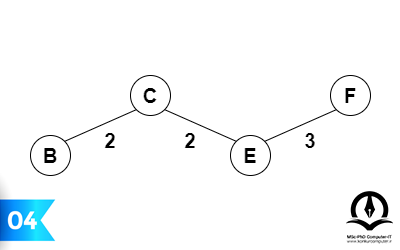
کوتاه‌ترین یالی (یال با کمترین وزن) که درخت فعلی را به یک راس جدید متصل میکند را پیدا می‌کنیم و به درخت اضافه می‌کنیم. این کار را تا زمانی که تمام رئوس گراف در درخت باشند ادامه می‌دهیم و به این صورت درخت پوشای کمینه را می‌سازیم.
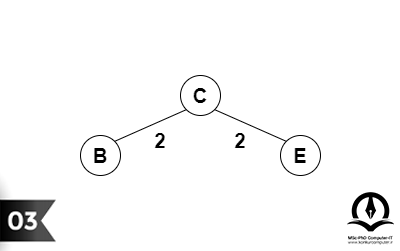
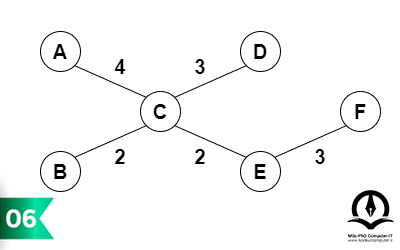
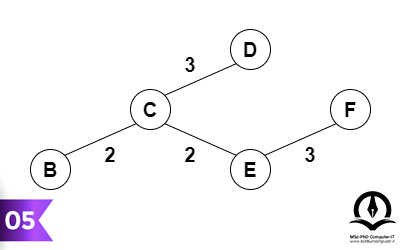
نتیجه نهایی درخت پوشای کمینه‌ای است که با استفاده از الگوریتم پریم به‌دست آمده است.
پیاده‌سازی الگوریتم پریم
شبه کد الگوریتم پریم زیر نشان میدهد که چگونه دو مجموعه از رئوس U و V-U ایجاد می‌کنیم. مجموعه U شامل لیست رئوسی است که بازدید شده‌اند و در درخت قرار گرفته‌اند و مجموعه V-U لیست رئوسی است که بازدید نشده‌اند. رئوس را از مجموعه V-U به مجموعه U یک به یک با اتصال یال کموزن منتقل می‌کنیم.
T = ∅;
U = { 1 };
while (U ≠ V)
let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U;
T = T ∪ {(u, v)}
U = U ∪ {v}
در ادامه پیاده‌سازی الگوریتم پریم در زبان های برنامه نویسی مختلف آورده شده است. توجه کنید که در پیاده‌سازی‌های زیر ما با استفاده از ماتریس مجاورت، الگوریتم پریم را پیاده‌سازی کرده‌ایم ولی می‌توان این الگوریتم را با استفاده از لیست مجاورت هم پیاده‌سازی کرد.
Python
# Prim's Algorithm in Python
INF = 9999999
# number of vertices in graph
V = 5
# create a 2d array of size 5x5
# for adjacency matrix to represent graph
G = [[0, 9, 75, 0, 0],
[9, 0, 95, 19, 42],
[75, 95, 0, 51, 66],
[0, 19, 51, 0, 31],
[0, 42, 66, 31, 0]]
# create a array to track selected vertex
# selected will become true otherwise false
selected = [0, 0, 0, 0, 0]
# set number of edge to 0
no_edge = 0
# the number of egde in minimum spanning tree will be
# always less than(V - 1), where V is number of vertices in
# graph
# choose 0th vertex and make it true
selected[0] = True
# print for edge and weight
print("Edge : Weight\n")
while (no_edge < V - 1):
# For every vertex in the set S, find the all adjacent vertices
#, calculate the distance from the vertex selected at step 1.
# if the vertex is already in the set S, discard it otherwise
# choose another vertex nearest to selected vertex at step 1.
minimum = INF
x = 0
y = 0
for i in range(V):
if selected[i]:
for j in range(V):
if ((not selected[j]) and G[i][j]):
# not in selected and there is an edge
if minimum > G[i][j]:
minimum = G[i][j]
x = i
y = j
print(str(x) + "-" + str(y) + ":" + str(G[x][y]))
selected[y] = True
no_edge += 1
Java
// Prim's Algorithm in Java
import java.util.Arrays;
class PGraph {
public void Prim(int G[][], int V) {
int INF = 9999999;
int no_edge; // number of edge
// create a array to track selected vertex
// selected will become true otherwise false
boolean[] selected = new boolean[V];
// set selected false initially
Arrays.fill(selected, false);
// set number of edge to 0
no_edge = 0;
// the number of egde in minimum spanning tree will be
// always less than (V -1), where V is number of vertices in
// graph
// choose 0th vertex and make it true
selected[0] = true;
// print for edge and weight
System.out.println("Edge : Weight");
while (no_edge < V - 1) {
// For every vertex in the set S, find the all adjacent vertices
// , calculate the distance from the vertex selected at step 1.
// if the vertex is already in the set S, discard it otherwise
// choose another vertex nearest to selected vertex at step 1.
int min = INF;
int x = 0; // row number
int y = 0; // col number
for (int i = 0; i < V; i++) {
if (selected[i] == true) {
for (int j = 0; j < V; j++) {
// not in selected and there is an edge
if (!selected[j] && G[i][j] != 0) {
if (min > G[i][j]) {
min = G[i][j];
x = i;
y = j;
}
}
}
}
}
System.out.println(x + " - " + y + " : " + G[x][y]);
selected[y] = true;
no_edge++;
}
}
public static void main(String[] args) {
PGraph g = new PGraph();
// number of vertices in grapj
int V = 5;
// create a 2d array of size 5x5
// for adjacency matrix to represent graph
int[][] G = { { 0, 9, 75, 0, 0 }, { 9, 0, 95, 19, 42 }, { 75, 95, 0, 51, 66 }, { 0, 19, 51, 0, 31 },
{ 0, 42, 66, 31, 0 } };
g.Prim(G, V);
}
}
C
// Prim's Algorithm in C
#include<stdio.h>
#include<stdbool.h>
#define INF 9999999
// number of vertices in graph
#define V 5
// create a 2d array of size 5x5
//for adjacency matrix to represent graph
int G[V][V] = {
{0, 9, 75, 0, 0},
{9, 0, 95, 19, 42},
{75, 95, 0, 51, 66},
{0, 19, 51, 0, 31},
{0, 42, 66, 31, 0}};
int main() {
int no_edge; // number of edge
// create a array to track selected vertex
// selected will become true otherwise false
int selected[V];
// set selected false initially
memset(selected, false, sizeof(selected));
// set number of edge to 0
no_edge = 0;
// the number of egde in minimum spanning tree will be
// always less than (V -1), where V is number of vertices in
//graph
// choose 0th vertex and make it true
selected[0] = true;
int x; // row number
int y; // col number
// print for edge and weight
printf("Edge : Weight\n");
while (no_edge < V - 1) {
//For every vertex in the set S, find the all adjacent vertices
// , calculate the distance from the vertex selected at step 1.
// if the vertex is already in the set S, discard it otherwise
//choose another vertex nearest to selected vertex at step 1.
int min = INF;
x = 0;
y = 0;
for (int i = 0; i < V; i++) {
if (selected[i]) {
for (int j = 0; j < V; j++) {
if (!selected[j] && G[i][j]) { // not in selected and there is an edge
if (min > G[i][j]) {
min = G[i][j];
x = i;
y = j;
}
}
}
}
}
printf("%d - %d : %d\n", x, y, G[x][y]);
selected[y] = true;
no_edge++;
}
return 0;
}
C++
// Prim's Algorithm in C++
#include <cstring>
#include <iostream>
using namespace std;
#define INF 9999999
// number of vertices in grapj
#define V 5
// create a 2d array of size 5x5
//for adjacency matrix to represent graph
int G[V][V] = {
{0, 9, 75, 0, 0},
{9, 0, 95, 19, 42},
{75, 95, 0, 51, 66},
{0, 19, 51, 0, 31},
{0, 42, 66, 31, 0}};
int main() {
int no_edge; // number of edge
// create a array to track selected vertex
// selected will become true otherwise false
int selected[V];
// set selected false initially
memset(selected, false, sizeof(selected));
// set number of edge to 0
no_edge = 0;
// the number of egde in minimum spanning tree will be
// always less than (V -1), where V is number of vertices in
//graph
// choose 0th vertex and make it true
selected[0] = true;
int x; // row number
int y; // col number
// print for edge and weight
cout << "Edge"
<< " : "
<< "Weight";
cout << endl;
while (no_edge < V - 1) {
//For every vertex in the set S, find the all adjacent vertices
// , calculate the distance from the vertex selected at step 1.
// if the vertex is already in the set S, discard it otherwise
//choose another vertex nearest to selected vertex at step 1.
int min = INF;
x = 0;
y = 0;
for (int i = 0; i < V; i++) {
if (selected[i]) {
for (int j = 0; j < V; j++) {
if (!selected[j] && G[i][j]) { // not in selected and there is an edge
if (min > G[i][j]) {
min = G[i][j];
x = i;
y = j;
}
}
}
}
}
cout << x << " - " << y << " : " << G[x][y];
cout << endl;
selected[y] = true;
no_edge++;
}
return 0;
}
مقایسه الگوریتم پریم و کروسکال
الگوریتم کروسکال یکی دیگر از الگوریتم‌های محبوب درخت پوشای کمینه است که از منطق متفاوتی برای یافتن درخت پوشای کمینه یک گراف استفاده میکند. الگوریتم کروسکال به‌جای شروع از یک راس، تمام یالها را از وزن کم به زیاد مرتب میکند و به اضافه کردن پایین‌ترین یالها ادامه میدهد و یال‌هایی را که چرخه ایجاد می‌کنند نادیده می‌گیرد.
پیچیدگی زمانی الگوریتم پریم
پیچیدگی زمانی الگوریتم پریم از مرتبه O(E log V) است که E تعداد یالها و V تعداد رئوس گراف را نشان میدهد.
کاربردهای الگوریتم پریم
از جمله کاربردهای الگوریتم پریم می‌توان به موارد زیر اشاره کرد:
- سیم‌کشی برق
- در شبکه های کامپیوتری (اتصال LAN)
جمع‌بندی
الگوریتم پریم یک تکنیک قدرتمند برای حل مسئله درخت پوشای کمینه در نظریه است. کارایی و مقیاس پذیری آن، آن را به ابزاری ارزشمند برای برنامه‌های کاربردی دنیای واقعی، از جمله طراحی شبکه، بهینه‌سازی لجستیک و تجزیه و تحلیل داده‌ها تبدیل میکند.
الگوریتم پریم چیست؟
الگوریتم Prim یک الگوریتم حریصانه است که برای یافتن درخت پوشای کمینه برای یک گراف استفاده میشود. این زیرمجموعه درختی را تشکیل میدهد که شامل هر رأس میشود و وزن کل تمام یالهای درخت حداقل میباشد.
پیچیدگی الگوریتم پریم چیست؟
پیچیدگی زمانی الگوریتم پریم از مرتبه O(E log V) است که E تعداد یالها و V تعداد رئوس گراف را نشان میدهد.
تفاوت الگوریتم پریم و کروسکال چیست؟
الگوریتم Prim راس ریشه را در ابتدا انتخاب میکند و سپس از راس به راس مجاور حرکت میکند. در سوی دیگر، الگوریتم Kruskal از یال با کمترین وزن شروع کرده و یالهای کموزن بعدی را به درخت اضافه میکند.
الگوریتم پریم از چه رویکردی برای حل مسئله استفاده میکند؟
الگوریتم Prim برای یافتن درخت پوشای کمینه (مثل الگوریتم Kruskal) از رویکرد حریصانه استفاده میکند.
الگوریتم پریم بهتر است یا کروسکال؟
مزیت الگوریتم پریم پیچیدگی زمانی آن است که از الگوریتم کروسکال بهتر است؛ بنابراین الگوریتم پریم هنگام برخورد با گرافهای متراکم که دارای یالهای زیادی هستند مفید است؛ با این حال، الگوریتم پریم به ما اجازه نمیدهد تا کنترل زیادی روی یالهای انتخاب شده، زمانی که چندین یال با وزن یکسان رخ میدهند، داشته باشیم.
مطالب مرتبط
همه مقالات
