برای شروع حرفهای کنکور ارشد کامپیوتر،آیتی و علوم کامپیوتر حتما روی عکس زیر کلیک کنید تا در کانال کنکور کامپیوتر عضو شوید، در این کانال به معرفی بهترین منابع کنکور ارشد،برنامه ریزی و مشاوره، معرفی گرایشها و هر آنچه برای موفقیت در کنکور ارشد نیاز دارید پرداخته شده است

الگوریتم کروسکال یا کراسکال یک الگوریتم درخت پوشای کمینه است که یک گراف وزندار را بهعنوان ورودی میگیرد و زیرمجموعه یالهای آن گرافگراف چیست، آموزش گراف از 0 تا 100 توسط دانشجو ارشد صنعتی شریف در این مقاله تمامی مطالب مربوط به گراف از 0 تا 100 تدریس شده است. مواردی همچون : گراف چیست؟ انواع گراف، گراف همبند، مکمل گراف، گراف کامل، گراف جهت دار، گراف بدون جهت، گراف ساده و ... را بهگونهای پیدا میکند که:
در این مقاله تمامی مطالب مربوط به گراف از 0 تا 100 تدریس شده است. مواردی همچون : گراف چیست؟ انواع گراف، گراف همبند، مکمل گراف، گراف کامل، گراف جهت دار، گراف بدون جهت، گراف ساده و ... را بهگونهای پیدا میکند که:
- درختی را تشکیل دهید که شامل هر رأس است.
- دارای حداقل مجموع وزنها در بین تمام درختانی است که میتوان از گراف تشکیل داد.

در این آموزش نحوه عملکرد الگوریتم کروسکال را خواهید آموخت؛ همچنین نمونههای کارکردی از الگوریتم کروسکال را در پایتونزبان برنامه نویسی پایتون چیست؟ – نحوه شروع و دلایل محبوبیت زبان برنامه نویسی پایتون (Python) چیست؟ این مقاله عالی به بررسی دلایل محبوبیت پایتون، موارد استفاده از پایتون و نحوه شروع به برنامه نویسی پایتون پرداخته، جاواجاوا چیست؟ تعریف، معنی و ویژگی های جاوا (java) از 0تا100
زبان برنامه نویسی پایتون (Python) چیست؟ این مقاله عالی به بررسی دلایل محبوبیت پایتون، موارد استفاده از پایتون و نحوه شروع به برنامه نویسی پایتون پرداخته، جاواجاوا چیست؟ تعریف، معنی و ویژگی های جاوا (java) از 0تا100 جاوا یک زبان برنامه نویسی همه منظوره، مبتنی بر کلاس و شی گرا است که برای داشتن وابستگی های پیاده سازی کمتر طراحی شده است، زبان برنامه نویسی جاوا شبیه ++C است، Cزبان برنامه نویسی C – مزایا و کاربرد زبان C – فرق C و ++C
جاوا یک زبان برنامه نویسی همه منظوره، مبتنی بر کلاس و شی گرا است که برای داشتن وابستگی های پیاده سازی کمتر طراحی شده است، زبان برنامه نویسی جاوا شبیه ++C است، Cزبان برنامه نویسی C – مزایا و کاربرد زبان C – فرق C و ++C این مقاله عالی ابتدا توضیح میدهد که زبان برنامه نویسی c چیست، سپس به بررسی مزایا و معایب زبان C ، کاربردهای زبان سی ، و تفاوت بین C و ++C میپردازد و سی پلاس پلاسبرنامه نویسی سی پلاس پلاس چیست؟ مزایای برنامه نویسی C++؟
این مقاله عالی ابتدا توضیح میدهد که زبان برنامه نویسی c چیست، سپس به بررسی مزایا و معایب زبان C ، کاربردهای زبان سی ، و تفاوت بین C و ++C میپردازد و سی پلاس پلاسبرنامه نویسی سی پلاس پلاس چیست؟ مزایای برنامه نویسی C++؟ برنامه نویسی سی پلاس پلاس چیست و چه کاربردی دارد؟ این صفحه عالی به بررسی مزایای برنامه نویسی C++ پرداخته و نمونه هایی از کدهای زبان برنامه نویسی ++C را آورده خواهید دید.
برنامه نویسی سی پلاس پلاس چیست و چه کاربردی دارد؟ این صفحه عالی به بررسی مزایای برنامه نویسی C++ پرداخته و نمونه هایی از کدهای زبان برنامه نویسی ++C را آورده خواهید دید.
الگوریتم کروسکال
این الگوریتمالگوریتم چیست به زبان ساده و با مثال های فراوان در این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد در دستهای از الگوریتمها بهنام الگوریتمهای حریصانه قرار میگیرد که بهینه محلی را به امید یافتن یک بهینه جهانی پیدا میکنند. در الگوریتم کراسکال از یالهایی با کمترین وزن شروع میکنیم و به اضافه کردن یالها ادامه میدهیم تا به هدف خود برسیم.
در این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد در دستهای از الگوریتمها بهنام الگوریتمهای حریصانه قرار میگیرد که بهینه محلی را به امید یافتن یک بهینه جهانی پیدا میکنند. در الگوریتم کراسکال از یالهایی با کمترین وزن شروع میکنیم و به اضافه کردن یالها ادامه میدهیم تا به هدف خود برسیم.
مراحل پیاده سازی الگوریتم کروسکال به شرح زیر است:
- تمام یالها را از وزن کم تا زیاد مرتب کنید.
- یال را با کمترین وزن بردارید و به درخت پوشا اضافه کنید. اگر با اضافه کردن یال یک دور ایجاد شد، این یال را حذف کنید.
- به اضافه کردن یالها ادامه دهید تا به همه رئوس برسیم.
مثالی از الگوریتم کروسکال
گراف وزندار زیر را در نظر بگیرید:

میخواهیم درخت پوشای کمینه این گراف را بهدست آوریم (توجه کنید درخت پوشای کمینه در یک گراف لزوما یکتا نیست). پس از مرتب کردن یالها بهترتیب وزن از کمترین وزن شروع به ساختن درخت میکنیم. اگر در این مرحله وزن دو گره برابر بود، یکی از آنها را انتخاب میکنیم. این کار را تا وقتی که تمام رئوس در درخت باشند ادامه میدهیم. اگر اضافه کردن یک یال در درخت باعث ایجاد دور شود، آن یال را رد میکنیم.
مراحل انجام این الگوریتم در شکلهای زیر به ترتیب تا رسیدن به درخت پوشای کمینه آورده شده است:
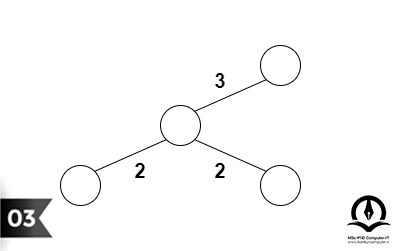
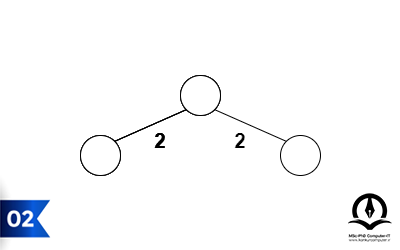
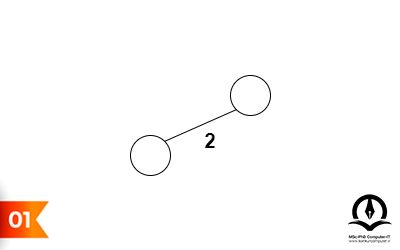
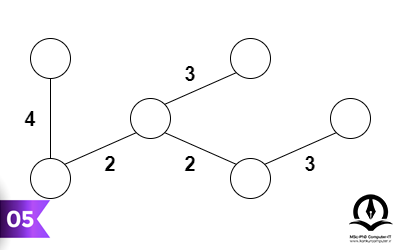
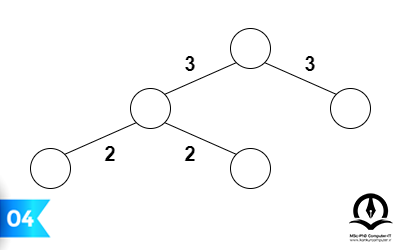
پیادهسازی الگوریتم کروسکال
یکی از مسائل مهم در درخت پوشای کمینه بررسی این است که آیا اضافه کردن یک یال باعث ایجاد دور میشود یا خیر؟ رایج ترین راه برای پیدا کردن این موضوع، الگوریتمی به نام Union Find است. الگوریتم Union-Find رئوس را به خوشهها تقسیم میکند و به ما اجازه میدهد بررسی کنیم که آیا دو راس به یک خوشه تعلق دارند یا نه و از این رو تصمیم میگیریم که آیا اضافه کردن یک یال باعث ایجاد دور میشود یا خیر.
شبه کد الگوریتم کروسکال به شکل زیر است:
KRUSKAL(G):
A = ∅
For each vertex v ∈ G.V:
MAKE-SET(v)
For each edge (u, v) ∈ G.E ordered by increasing order by weight(u, v):
if FIND-SET(u) ≠ FIND-SET(v):
A = A ∪ {(u, v)}
UNION(u, v)
return A
در ادامه پیادهسازی الگوریتم کروسکال با زبان های برنامه نویسیزبان های برنامه نویسی چیست؟ این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده مختلف آورده شده است:
این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده مختلف آورده شده است:
Python
# Kruskal's algorithm in Python
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = []
def add_edge(self, u, v, w):
self.graph.append([u, v, w])
# Search function
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
def apply_union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
else:
parent[yroot] = xroot
rank[xroot] += 1
# Applying Kruskal algorithm
def kruskal_algo(self):
result = []
i, e = 0, 0
self.graph = sorted(self.graph, key=lambda item: item[2])
parent = []
rank = []
for node in range(self.V):
parent.append(node)
rank.append(0)
while e < self.V - 1:
u, v, w = self.graph[i]
i = i + 1
x = self.find(parent, u)
y = self.find(parent, v)
if x != y:
e = e + 1
result.append([u, v, w])
self.apply_union(parent, rank, x, y)
for u, v, weight in result:
print("%d - %d: %d" % (u, v, weight))
g = Graph(6)
g.add_edge(0, 1, 4)
g.add_edge(0, 2, 4)
g.add_edge(1, 2, 2)
g.add_edge(1, 0, 4)
g.add_edge(2, 0, 4)
g.add_edge(2, 1, 2)
g.add_edge(2, 3, 3)
g.add_edge(2, 5, 2)
g.add_edge(2, 4, 4)
g.add_edge(3, 2, 3)
g.add_edge(3, 4, 3)
g.add_edge(4, 2, 4)
g.add_edge(4, 3, 3)
g.add_edge(5, 2, 2)
g.add_edge(5, 4, 3)
g.kruskal_algo()
Java
// Kruskal's algorithm in Java
import java.util.*;
class Graph {
class Edge implements Comparable<Edge> {
int src, dest, weight;
public int compareTo(Edge compareEdge) {
return this.weight - compareEdge.weight;
}
};
// Union
class subset {
int parent, rank;
};
int vertices, edges;
Edge edge[];
// Graph creation
Graph(int v, int e) {
vertices = v;
edges = e;
edge = new Edge[edges];
for (int i = 0; i < e; ++i)
edge[i] = new Edge();
}
int find(subset subsets[], int i) {
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
void Union(subset subsets[], int x, int y) {
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if (subsets[xroot].rank < subsets[yroot].rank) subsets[xroot].parent = yroot; else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Applying Krushkal Algorithm
void KruskalAlgo() {
Edge result[] = new Edge[vertices];
int e = 0;
int i = 0;
for (i = 0; i < vertices; ++i)
result[i] = new Edge();
// Sorting the edges
Arrays.sort(edge);
subset subsets[] = new subset[vertices];
for (i = 0; i < vertices; ++i)
subsets[i] = new subset();
for (int v = 0; v < vertices; ++v) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
i = 0;
while (e < vertices - 1) {
Edge next_edge = new Edge();
next_edge = edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
if (x != y) {
result[e++] = next_edge;
Union(subsets, x, y);
}
}
for (i = 0; i < e; ++i)
System.out.println(result[i].src + " - " + result[i].dest + ": " + result[i].weight);
}
public static void main(String[] args) {
int vertices = 6; // Number of vertices
int edges = 8; // Number of edges
Graph G = new Graph(vertices, edges);
G.edge[0].src = 0;
G.edge[0].dest = 1;
G.edge[0].weight = 4;
G.edge[1].src = 0;
G.edge[1].dest = 2;
G.edge[1].weight = 4;
G.edge[2].src = 1;
G.edge[2].dest = 2;
G.edge[2].weight = 2;
G.edge[3].src = 2;
G.edge[3].dest = 3;
G.edge[3].weight = 3;
G.edge[4].src = 2;
G.edge[4].dest = 5;
G.edge[4].weight = 2;
G.edge[5].src = 2;
G.edge[5].dest = 4;
G.edge[5].weight = 4;
G.edge[6].src = 3;
G.edge[6].dest = 4;
G.edge[6].weight = 3;
G.edge[7].src = 5;
G.edge[7].dest = 4;
G.edge[7].weight = 3;
G.KruskalAlgo();
}
}
C
// Kruskal's algorithm in C
#include <stdio.h>
#define MAX 30
typedef struct edge {
int u, v, w;
} edge;
typedef struct edge_list {
edge data[MAX];
int n;
} edge_list;
edge_list elist;
int Graph[MAX][MAX], n;
edge_list spanlist;
void kruskalAlgo();
int find(int belongs[], int vertexno);
void applyUnion(int belongs[], int c1, int c2);
void sort();
void print();
// Applying Krushkal Algo
void kruskalAlgo() {
int belongs[MAX], i, j, cno1, cno2;
elist.n = 0;
for (i = 1; i < n; i++)
for (j = 0; j < i; j++) {
if (Graph[i][j] != 0) {
elist.data[elist.n].u = i;
elist.data[elist.n].v = j;
elist.data[elist.n].w = Graph[i][j];
elist.n++;
}
}
sort();
for (i = 0; i < n; i++)
belongs[i] = i;
spanlist.n = 0;
for (i = 0; i < elist.n; i++) {
cno1 = find(belongs, elist.data[i].u);
cno2 = find(belongs, elist.data[i].v);
if (cno1 != cno2) {
spanlist.data[spanlist.n] = elist.data[i];
spanlist.n = spanlist.n + 1;
applyUnion(belongs, cno1, cno2);
}
}
}
int find(int belongs[], int vertexno) {
return (belongs[vertexno]);
}
void applyUnion(int belongs[], int c1, int c2) {
int i;
for (i = 0; i < n; i++)
if (belongs[i] == c2)
belongs[i] = c1;
}
// Sorting algo
void sort() {
int i, j;
edge temp;
for (i = 1; i < elist.n; i++)
for (j = 0; j < elist.n - 1; j++) if (elist.data[j].w > elist.data[j + 1].w) {
temp = elist.data[j];
elist.data[j] = elist.data[j + 1];
elist.data[j + 1] = temp;
}
}
// Printing the result
void print() {
int i, cost = 0;
for (i = 0; i < spanlist.n; i++) {
printf("\n%d - %d : %d", spanlist.data[i].u, spanlist.data[i].v, spanlist.data[i].w);
cost = cost + spanlist.data[i].w;
}
printf("\nSpanning tree cost: %d", cost);
}
int main() {
int i, j, total_cost;
n = 6;
Graph[0][0] = 0;
Graph[0][1] = 4;
Graph[0][2] = 4;
Graph[0][3] = 0;
Graph[0][4] = 0;
Graph[0][5] = 0;
Graph[0][6] = 0;
Graph[1][0] = 4;
Graph[1][1] = 0;
Graph[1][2] = 2;
Graph[1][3] = 0;
Graph[1][4] = 0;
Graph[1][5] = 0;
Graph[1][6] = 0;
Graph[2][0] = 4;
Graph[2][1] = 2;
Graph[2][2] = 0;
Graph[2][3] = 3;
Graph[2][4] = 4;
Graph[2][5] = 0;
Graph[2][6] = 0;
Graph[3][0] = 0;
Graph[3][1] = 0;
Graph[3][2] = 3;
Graph[3][3] = 0;
Graph[3][4] = 3;
Graph[3][5] = 0;
Graph[3][6] = 0;
Graph[4][0] = 0;
Graph[4][1] = 0;
Graph[4][2] = 4;
Graph[4][3] = 3;
Graph[4][4] = 0;
Graph[4][5] = 0;
Graph[4][6] = 0;
Graph[5][0] = 0;
Graph[5][1] = 0;
Graph[5][2] = 2;
Graph[5][3] = 0;
Graph[5][4] = 3;
Graph[5][5] = 0;
Graph[5][6] = 0;
kruskalAlgo();
print();
}
C++
// Kruskal's algorithm in C++
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
#define edge pair<int, int>
class Graph {
private:
vector > G; // graph
vector > T; // mst
int *parent;
int V; // number of vertices/nodes in graph
public:
Graph(int V);
void AddWeightedEdge(int u, int v, int w);
int find_set(int i);
void union_set(int u, int v);
void kruskal();
void print();
};
Graph::Graph(int V) {
parent = new int[V];
//i 0 1 2 3 4 5
//parent[i] 0 1 2 3 4 5
for (int i = 0; i < V; i++)
parent[i] = i;
G.clear();
T.clear();
}
void Graph::AddWeightedEdge(int u, int v, int w) {
G.push_back(make_pair(w, edge(u, v)));
}
int Graph::find_set(int i) {
// If i is the parent of itself
if (i == parent[i])
return i;
else
// Else if i is not the parent of itself
// Then i is not the representative of his set,
// so we recursively call Find on its parent
return find_set(parent[i]);
}
void Graph::union_set(int u, int v) {
parent[u] = parent[v];
}
void Graph::kruskal() {
int i, uRep, vRep;
sort(G.begin(), G.end()); // increasing weight
for (i = 0; i < G.size(); i++) {
uRep = find_set(G[i].second.first);
vRep = find_set(G[i].second.second);
if (uRep != vRep) {
T.push_back(G[i]); // add to tree
union_set(uRep, vRep);
}
}
}
void Graph::print() {
cout << "Edge :"
<< " Weight" << endl;
for (int i = 0; i < T.size(); i++) {
cout << T[i].second.first << " - " << T[i].second.second << " : "
<< T[i].first;
cout << endl;
}
}
int main() {
Graph g(6);
g.AddWeightedEdge(0, 1, 4);
g.AddWeightedEdge(0, 2, 4);
g.AddWeightedEdge(1, 2, 2);
g.AddWeightedEdge(1, 0, 4);
g.AddWeightedEdge(2, 0, 4);
g.AddWeightedEdge(2, 1, 2);
g.AddWeightedEdge(2, 3, 3);
g.AddWeightedEdge(2, 5, 2);
g.AddWeightedEdge(2, 4, 4);
g.AddWeightedEdge(3, 2, 3);
g.AddWeightedEdge(3, 4, 3);
g.AddWeightedEdge(4, 2, 4);
g.AddWeightedEdge(4, 3, 3);
g.AddWeightedEdge(5, 2, 2);
g.AddWeightedEdge(5, 4, 3);
g.kruskal();
g.print();
return 0;
}
مقایسه الگوریتم کروسکال و الگوریتم پریم
الگوریتم Prim یکی دیگر از الگوریتمهای محبوب درخت پوشای کمینه است که از منطق متفاوتی برای یافتن درخت پوشای کمینه گراف استفاده میکند. این الگوریتم، بهجای شروع از یک یال، از یک راس شروع میکند و به اضافه کردن یالهای کموزن که در درخت نیستند، ادامه میدهد تا زمانی که همه راسها پوشانده شوند.
پچیدگی زمانی الگوریتم کروسکال
پیچیدگی زمانی الگوریتم کروسکال از مرتبه O(E log E) است که E تعداد یالهای گراف است.
کاربردهای الگوریتم کروسکال
از جمله کاربردهای الگوریتم کروسکال میتوان به موارد زیر اشاره کرد:
جمعبندی
الگوریتم کروسکال یک تکنیک قدرتمند برای حل مسئله درخت پوشای کمینه در نظریه گراف است. کارایی و مقیاس پذیری آن، آن را به ابزاری ارزشمند برای برنامههای کاربردی دنیای واقعی، از جمله طراحی شبکه، بهینهسازی لجستیک و تجزیه و تحلیل دادهها تبدیل می کند.
الگوریتم کروسکال چیست؟
الگوریتم کروسکال یک الگوریتم درخت پوشای کمینه است که یک گراف را بهعنوان ورودی میگیرد و زیرمجموعه یالهای آن گراف را پیدا میکند. این زیرمجموعه درختی را تشکیل میدهد که شامل هر رأس می شود و وزن کل تمام یالهای درخت حداقل میباشد.
مراحل الگوریتم کروسکال چیست؟
مراحل پیاده سازی الگوریتم کروسکال به شرح زیر است:
تمام یالها را از وزن کم تا زیاد مرتب کنید.
یال با کمترین وزن را بردارید و به درخت پوشا اضافه کنید. اگر با اضافه کردن یال یک دور ایجاد شد، این یال را رد کنید.
به اضافه کردن یالها ادامه دهید تا همه رئوس در درخت قرار گیرند
تفاوت الگوریتم پریم و کروسکال چیست؟
الگوریتم Prim راس ریشه را در ابتدا انتخاب می کند و سپس از راس به راس مجاور حرکت میکند. در سوی دیگر، الگوریتم Kruskal از یال با کمترین وزن شروع کرده و یالهای کم وزن بعدی را به درخت اضافه میکند.
پیچیدگی زمانی الگوریتم کروسکال چیست؟
پیچیدگی زمانی الگوریتم کروسکال از مرتبه O(E log E) است که E تعداد یالهای گراف است.









































