برای شروع حرفهای کنکور ارشد کامپیوتر،آیتی و علوم کامپیوتر حتما روی عکس زیر کلیک کنید تا در کانال کنکور کامپیوتر عضو شوید، در این کانال به معرفی بهترین منابع کنکور ارشد،برنامه ریزی و مشاوره، معرفی گرایشها و هر آنچه برای موفقیت در کنکور ارشد نیاز دارید پرداخته شده است

درخت های جستجوی دودویی یا BST، ساختمان دادهآموزش ساختمان داده و الگوریتم هر ساختمان داده یک نوع فرمت ذخیرهسازی و مدیریت دادهها در کامپیوتر است، که امکان دسترسی و اصلاح کارآمد آن دادهها را برای یکسری از الگوریتمها و کاربردها فراهم میکند، در این صفحه به بررسی و آموزش ساختمان داده و الگوریتم پرداخته شده است هایی هستند که اغلب برای ذخیره و بازیابی بهینه دادهها استفاده میشوند. در این مقاله، بررسی خواهیم کرد که درخت های جستجوی دودویی چه هستند، چگونه کار میکنند و چرا کارآمد هستند؛ همچنین به برخی از مزایا و محدودیتهای درخت های جستجوی دودویی و نحوه استفاده از آنها در کاربردهای عملی خواهیم پرداخت. درخت جستجوی دودویی یک ساختمان دادهای است که بهسرعت به ما امکان میدهد فهرست مرتب شدهای از اعداد را ذخیره کنیم. در واقع لازم است بگوییم:
هر ساختمان داده یک نوع فرمت ذخیرهسازی و مدیریت دادهها در کامپیوتر است، که امکان دسترسی و اصلاح کارآمد آن دادهها را برای یکسری از الگوریتمها و کاربردها فراهم میکند، در این صفحه به بررسی و آموزش ساختمان داده و الگوریتم پرداخته شده است هایی هستند که اغلب برای ذخیره و بازیابی بهینه دادهها استفاده میشوند. در این مقاله، بررسی خواهیم کرد که درخت های جستجوی دودویی چه هستند، چگونه کار میکنند و چرا کارآمد هستند؛ همچنین به برخی از مزایا و محدودیتهای درخت های جستجوی دودویی و نحوه استفاده از آنها در کاربردهای عملی خواهیم پرداخت. درخت جستجوی دودویی یک ساختمان دادهای است که بهسرعت به ما امکان میدهد فهرست مرتب شدهای از اعداد را ذخیره کنیم. در واقع لازم است بگوییم:
- درخت دودویی نامیده میشود؛ زیرا هر گره درخت حداکثر دو فرزند دارد.
- درخت جستجو نامیده میشود؛ زیرا میتوان از آن برای جستجوی وجود یک عدد در زمان O(log(n)) استفاده کرد.
خواصی که یک درخت جستجوی دودویی را از یک درخت باینری معمولی جدا میکند عبارتاند از:
- تمام گرههای زیر درخت سمت چپ کمتر از گره ریشه هستند.
- تمام گرههای زیر درخت سمت راست بیشتر از گره ریشه هستند.
- هر دو زیر درخت هر گره نیز BST هستند، یعنی دو ویژگی فوق را دارند.
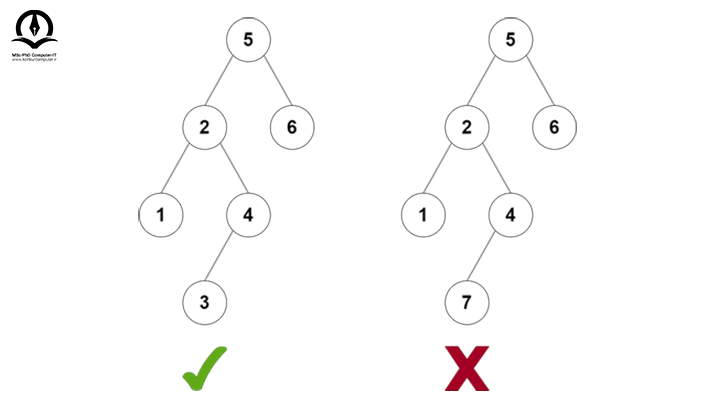
درخت دودویی سمت راست یک درخت جستجوی باینری نیست؛ زیرا زیر درخت سمت چپ گره "5" حاوی مقداری بزرگتر از آن است (گره 7). سه عملیات اساسی وجود دارد که میتوانید روی درخت جستجوی باینری انجام دهید که در ادامه به بررسی این عملیات میپردازیم.
عملیات اصلی درخت جستجوی دودویی
عملیات جستجو
این الگوریتمآموزش طراحی الگوریتم به زبان ساده درس طراحی الگوریتم یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است. هدف از این درس، معرفی روشهای مختلف طراحی الگوریتمها برای حل مسائل گوناگون است، در این صفحه به معرفی و آموزش طراحی الگوریتم پرداخته شده است. به خاصیت BST مربوط میشود که باید هر زیر درخت سمت چپ دارای مقادیر کوچکتر از ریشه و هر زیر درخت سمت راست دارای مقادیر بزرگتر از ریشه باشد.
درس طراحی الگوریتم یکی از مهمترین و بنیادیترین دروس رشته کامپیوتر است. هدف از این درس، معرفی روشهای مختلف طراحی الگوریتمها برای حل مسائل گوناگون است، در این صفحه به معرفی و آموزش طراحی الگوریتم پرداخته شده است. به خاصیت BST مربوط میشود که باید هر زیر درخت سمت چپ دارای مقادیر کوچکتر از ریشه و هر زیر درخت سمت راست دارای مقادیر بزرگتر از ریشه باشد.
اگر مقداری که به دنبال آن هستیم کوچکتر از ریشه باشد، با اطمینان میتوان گفت که مقدار در زیر درخت سمت راست نیست و فقط باید در زیر درخت سمت چپ جستجو کنیم؛ حال اگر مقدار بزرگتر از ریشه باشد، میتوانیم با اطمینان بگوییم که مقدار در زیر درخت سمت چپ نیست و ما فقط باید در زیر درخت سمت راست جستجو کنیم.
الگوریتم این عملیات بهصورت زیر است:
If root == NULL
return NULL;
If number == root->data
return root->data;
If number < root->data
return search(root->left)
If number > root->data
return search(root->right)
برای مثال درخت جستجوی دودویی زیر را در نظر بگیرید:
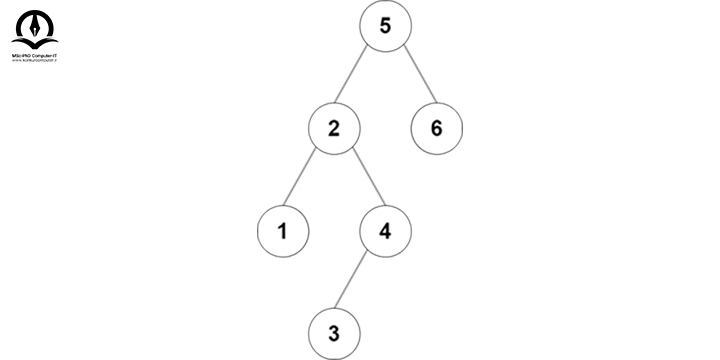
فرض کنید در این درخت به دنبال مقدار 3 هستیم، پس از گره شروع میکنیم:
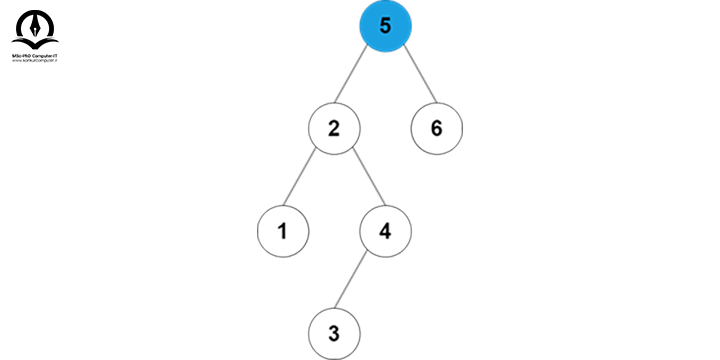
مقدار 5 از 3 بزرگتر است، پس باید به زیر درخت سمت چپ برویم:
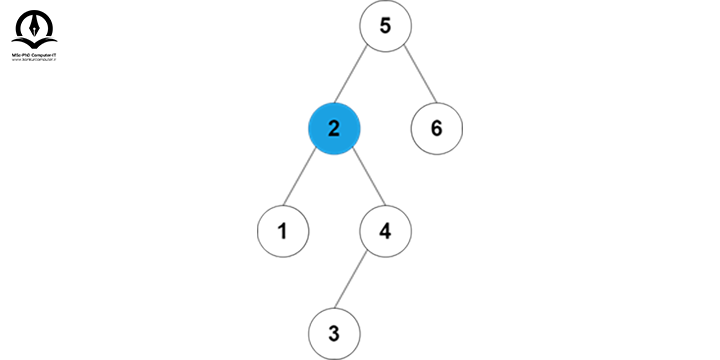
2 از 3 بزرگتر است، پس باید به زیر درخت سمت راست مقدار 2 برویم:
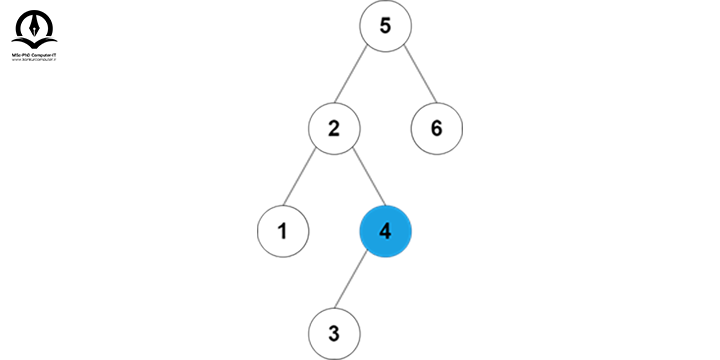
4 از 3 بزرگتر است، پس باید به زیر درخت سمت چپ 4 برویم:
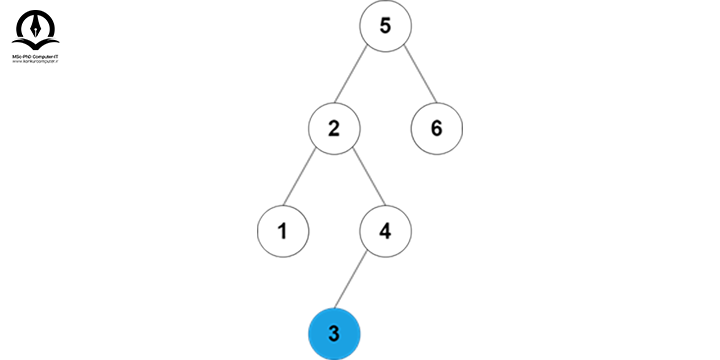
حال که مقدار 3 را پیدا کردیم آن را برمیگردانیم. اگر به گرهای میرسیدیم که باید به زیر درخت چپ یا راست آن میرفتیم؛ ولی آن زیر درخت وجود نداشت، آنگاه متوجه میشویم که مقدار موردنظر در درخت وجود ندارد.
عملیات درج
درج یک مقدار در موقعیت صحیح شبیه به جستجو است؛ زیرا ما سعی میکنیم این قانون را حفظ کنیم که زیر درخت سمت چپ کوچکتر از ریشه و زیر درخت سمت راست بزرگتر از ریشه است. بسته به مقدار به زیر درخت سمت راست یا زیر درخت سمت چپ ادامه میدهیم و وقتی به نقطهای رسیدیم که زیر درخت سمت چپ یا زیر درخت راست تهی شد، گره جدید را در آنجا قرار میدهیم.
الگوریتم عملیات درج به شکل زیر است:
If node == NULL
return createNode(data)
if (data < node->data)
node->left = insert(node->left, data);
else if (data > node->data)
node->right = insert(node->right, data);
return node;
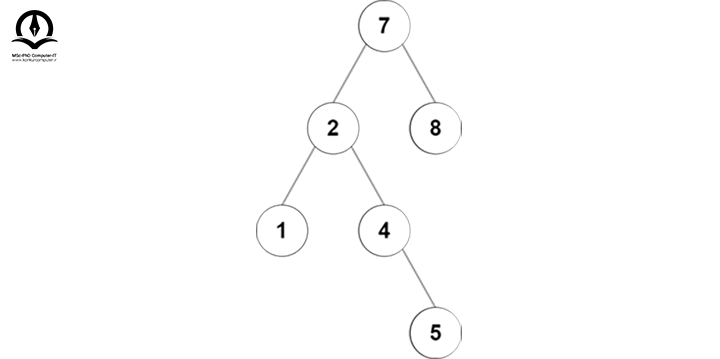
این الگوریتم پیچیدهتر از آن چیزی است که به نظر میرسد. بیایید سعی کنیم با یک مثال بررسی کنیم که چگونه یک عدد را به یک BST موجود اضافه میکنیم. درخت BST زیر را در نظر بگیرید:
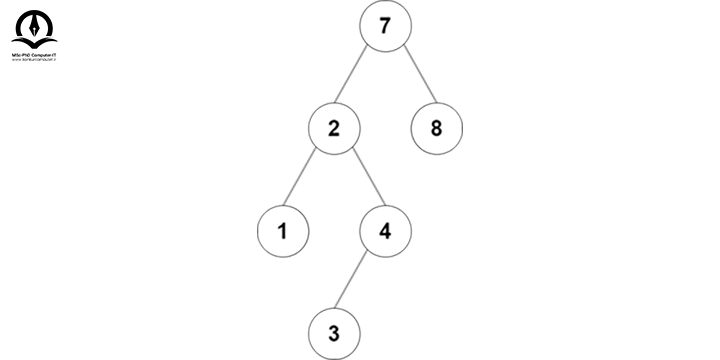
فرض کنید میخواهیم مقدار 5 را به این درخت اضافه کنیم، پس از ریشه شروع میکنیم:
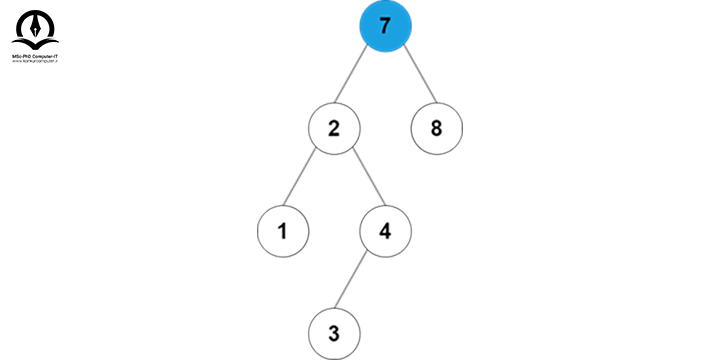
5 از 7 کوچکتر است، پس به زیر درخت سمت چپ میرویم:
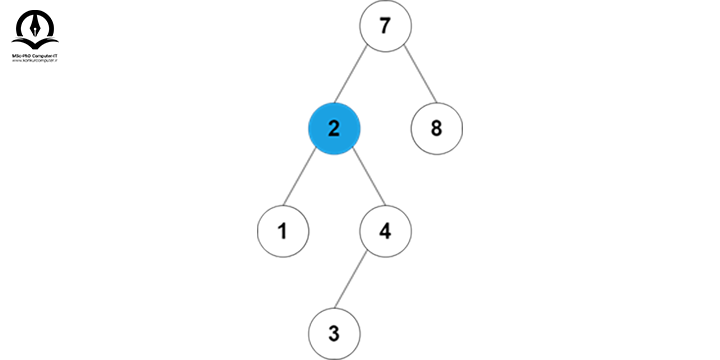
5 از 2 بزرگتر است، پس به زیر درخت سمت راست میرویم:
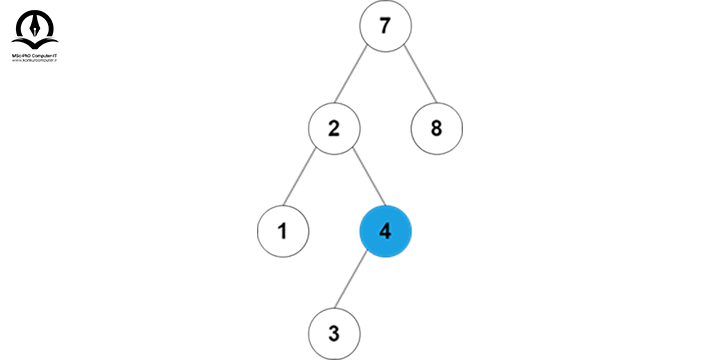
5 از 4 بزرگتر است، پس باید به زیر درخت سمت راست برویم؛ چون زیر درخت سمت راست 4 برابر NULL است، پس 5 را در آن درج میکنیم:
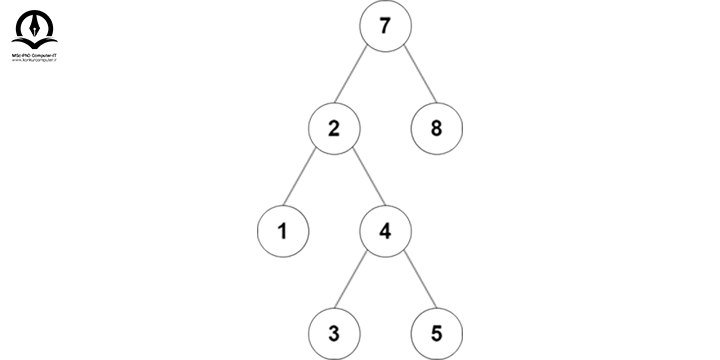
عملیات حذف
سه حالت برای حذف یک گره از درخت جستجوی باینری وجود دارد.
حالت اول
در حالت اول گرهای که باید حذف شود، گره برگ است. در چنین حالتی بهسادگی گره را از درخت حذف میکنیم.
حالت دوم
در حالت دوم گرهای که قرار است حذف شود، یک گره فرزند دارد. در چنین شرایطی مراحل زیر را دنبال میکنیم:
- آن گره را با گره فرزندش جایگزین میکنیم.
- گره فرزند را از موقعیت اصلی خود حذف میکنیم.
حالت سوم
در حالت سوم گرهای که باید حذف شود دو فرزند دارد. در چنین شرایطی مراحل زیر را دنبال میکنیم:
- گره بعدی آن گره را در پیمایش Inorder پیدا میکنیم.
- گره را با گره بعدی آن گره در پیمایش Inorder جایگزین میکنیم.
- گره بعدی آن گره در پیمایش Inorder را از موقعیت اصلی خود حذف میکنیم.
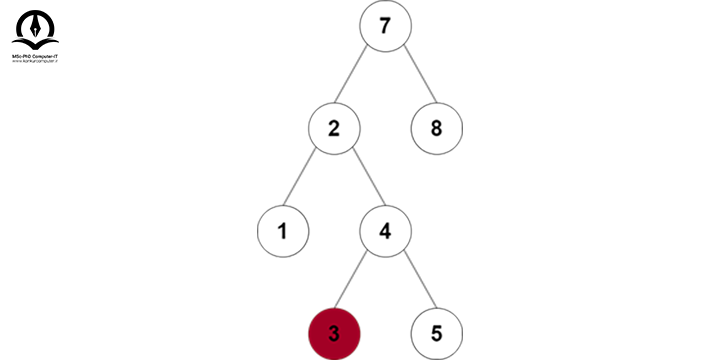
در درخت زیر فرض کنید میخواهیم گره 2 را حذف کنیم:
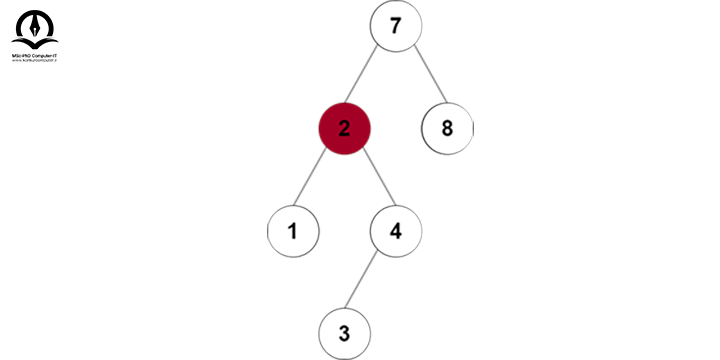
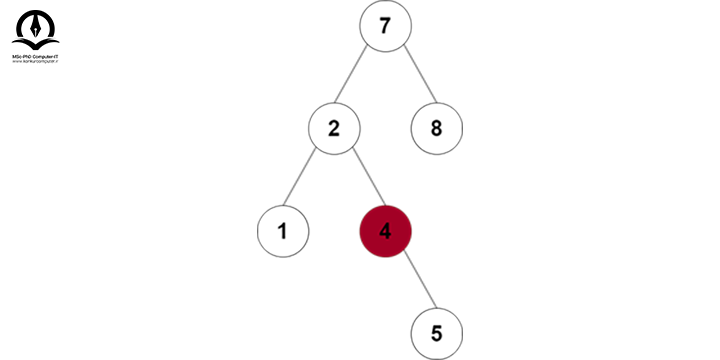
گره بعدی گره 2 در پیمایش Inorder، گره 3 خواهد بود پس آن را با گره 2 جایگزین میکنیم:
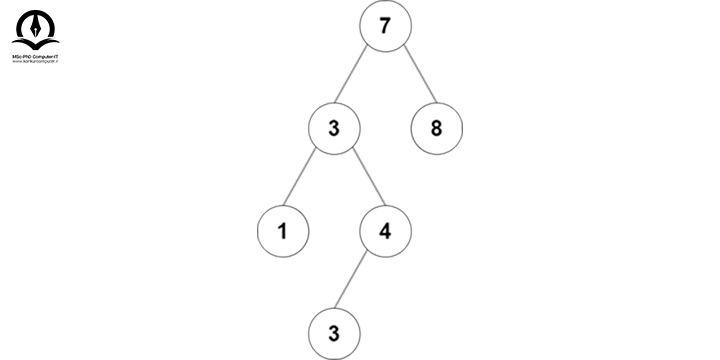
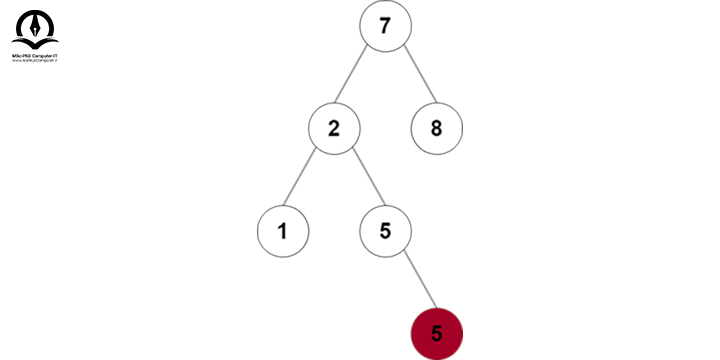
سپس گره 3 را از درخت حذف میکنیم:
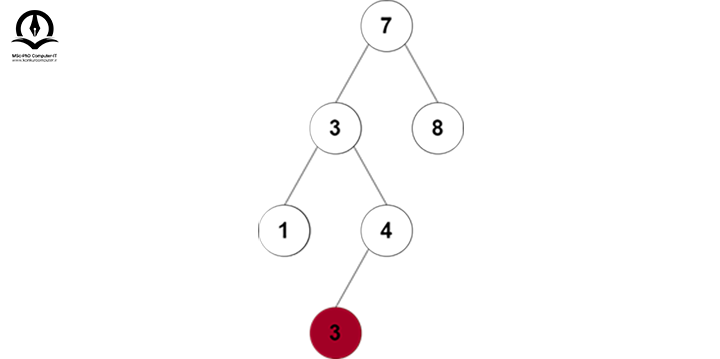
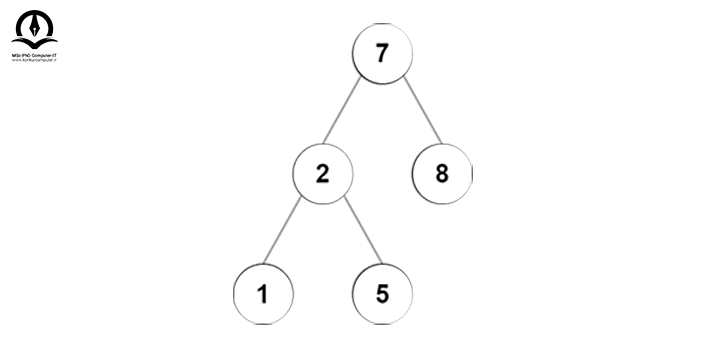
درخت نهایی به شکل زیر خواهد بود:
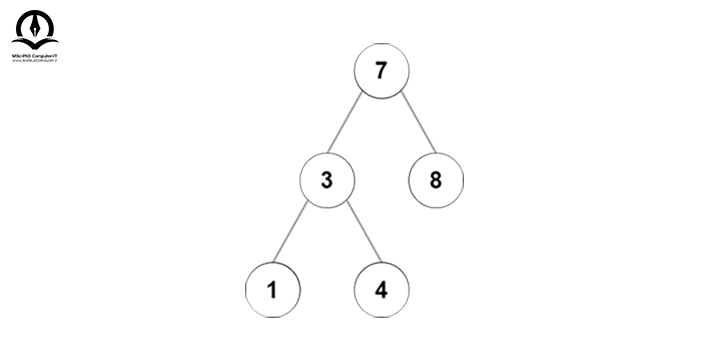
پیچیدگی زمانی و فضایی عملیات درخت جستجوی دودویی
عملیات درج، حذف و جستجو در بهترین حالت و حالت متوسط از مرتبه O(log n) و در بدترین حالت از مرتبه O(n) است و پیچیدگی فضایی برای تمام عملیات از مرتبه O(n) است.
پیادهسازی درخت جستجوی دودویی
در ادامه به پیادهسازی درخت جستجوی دودویی در زبان های برنامه نویسیزبان های برنامه نویسی چیست؟ این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده مانند پایتونزبان برنامه نویسی پایتون چیست؟ – نحوه شروع و دلایل محبوبیت
این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده مانند پایتونزبان برنامه نویسی پایتون چیست؟ – نحوه شروع و دلایل محبوبیت زبان برنامه نویسی پایتون (Python) چیست؟ این مقاله عالی به بررسی دلایل محبوبیت پایتون، موارد استفاده از پایتون و نحوه شروع به برنامه نویسی پایتون پرداخته، جاواجاوا چیست؟ تعریف، معنی و ویژگی های جاوا (java) از 0تا100
زبان برنامه نویسی پایتون (Python) چیست؟ این مقاله عالی به بررسی دلایل محبوبیت پایتون، موارد استفاده از پایتون و نحوه شروع به برنامه نویسی پایتون پرداخته، جاواجاوا چیست؟ تعریف، معنی و ویژگی های جاوا (java) از 0تا100 جاوا یک زبان برنامه نویسی همه منظوره، مبتنی بر کلاس و شی گرا است که برای داشتن وابستگی های پیاده سازی کمتر طراحی شده است، زبان برنامه نویسی جاوا شبیه ++C است، Cزبان برنامه نویسی C – مزایا و کاربرد زبان C – فرق C و ++C
جاوا یک زبان برنامه نویسی همه منظوره، مبتنی بر کلاس و شی گرا است که برای داشتن وابستگی های پیاده سازی کمتر طراحی شده است، زبان برنامه نویسی جاوا شبیه ++C است، Cزبان برنامه نویسی C – مزایا و کاربرد زبان C – فرق C و ++C این مقاله عالی ابتدا توضیح میدهد که زبان برنامه نویسی c چیست، سپس به بررسی مزایا و معایب زبان C ، کاربردهای زبان سی ، و تفاوت بین C و ++C میپردازد و سی پلاس پلاسبرنامه نویسی سی پلاس پلاس چیست؟ مزایای برنامه نویسی C++؟
این مقاله عالی ابتدا توضیح میدهد که زبان برنامه نویسی c چیست، سپس به بررسی مزایا و معایب زبان C ، کاربردهای زبان سی ، و تفاوت بین C و ++C میپردازد و سی پلاس پلاسبرنامه نویسی سی پلاس پلاس چیست؟ مزایای برنامه نویسی C++؟ برنامه نویسی سی پلاس پلاس چیست و چه کاربردی دارد؟ این صفحه عالی به بررسی مزایای برنامه نویسی C++ پرداخته و نمونه هایی از کدهای زبان برنامه نویسی ++C را آورده میپردازیم:
برنامه نویسی سی پلاس پلاس چیست و چه کاربردی دارد؟ این صفحه عالی به بررسی مزایای برنامه نویسی C++ پرداخته و نمونه هایی از کدهای زبان برنامه نویسی ++C را آورده میپردازیم:
Python
# Binary Search Tree operations in Python
# Create a node
class Node:
def __init__ (self, key):
self.key = key
self.left = None
self.right = None
# Inorder traversal
def inorder(root):
if root is not None:
# Traverse left
inorder(root.left)
# Traverse root
print(str(root.key) + "->", end=' ')
# Traverse right
inorder(root.right)
# Insert a node
def insert(node, key):
# Return a new node if the tree is empty
if node is None:
return Node(key)
# Traverse to the right place and insert the node
if key < node.key:
node.left = insert(node.left, key)
else:
node.right = insert(node.right, key)
return node
# Find the inorder successor
def minValueNode(node):
current = node
# Find the leftmost leaf
while(current.left is not None):
current = current.left
return current
# Deleting a node
def deleteNode(root, key):
# Return if the tree is empty
if root is None:
return root
# Find the node to be deleted
if key < root.key:
root.left = deleteNode(root.left, key)
elif(key > root.key):
root.right = deleteNode(root.right, key)
else:
# If the node is with only one child or no child
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
# If the node has two children,
# place the inorder successor in position of the node to be deleted
temp = minValueNode(root.right)
root.key = temp.key
# Delete the inorder successor
root.right = deleteNode(root.right, temp.key)
return root
root = None
root = insert(root, 8)
root = insert(root, 3)
root = insert(root, 1)
root = insert(root, 6)
root = insert(root, 7)
root = insert(root, 10)
root = insert(root, 14)
root = insert(root, 4)
print("Inorder traversal: ", end=' ')
inorder(root)
print("\nDelete 10")
root = deleteNode(root, 10)
print("Inorder traversal: ", end=' ')
inorder(root)
Java
// Binary Search Tree operations in Java
class BinarySearchTree {
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
Node root;
BinarySearchTree() {
root = null;
}
void insert(int key) {
root = insertKey(root, key);
}
// Insert key in the tree
Node insertKey(Node root, int key) {
// Return a new node if the tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// Traverse to the right place and insert the node
if (key < root.key)
root.left = insertKey(root.left, key);
else if (key > root.key)
root.right = insertKey(root.right, key);
return root;
}
void inorder() {
inorderRec(root);
}
// Inorder Traversal
void inorderRec(Node root) {
if (root != null) {
inorderRec(root.left);
System.out.print(root.key + " -> ");
inorderRec(root.right);
}
}
void deleteKey(int key) {
root = deleteRec(root, key);
}
Node deleteRec(Node root, int key) {
// Return if the tree is empty
if (root == null)
return root;
// Find the node to be deleted
if (key < root.key) root.left = deleteRec(root.left, key); else if (key > root.key)
root.right = deleteRec(root.right, key);
else {
// If the node is with only one child or no child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// If the node has two children
// Place the inorder successor in position of the node to be deleted
root.key = minValue(root.right);
// Delete the inorder successor
root.right = deleteRec(root.right, root.key);
}
return root;
}
// Find the inorder successor
int minValue(Node root) {
int minv = root.key;
while (root.left != null) {
minv = root.left.key;
root = root.left;
return minv;
// Driver Program to test above functions
public static void main(String [] args)
BinarySearchTree tree = new BinarySearchTree() ;
tree.insert(8);
tree.insert(3);
tree.insert(1);
tree.insert(6);
tree.insert(7);
tree.insert(10);
tree.insert(14);
tree.insert(4);
System.out.print("Inorder traversal: ") ;
tree.inorder() ;
System.out.println("\n\nAfter deleting 10") ;
tree.deleteKey(10);
System.out.print("Inorder traversal: ") ;
tree.inorder() ;
C
// Binary Search Tree operations in C
#include
#include
struct node
int key;
struct node *left, *right;
;
// Create a node
struct node *newNode(int item)
struct node *temp = (struct node *)malloc(sizeof(struct node)) ;
temp-> key = item;
temp-> left = temp-> right = NULL;
return temp;
// Inorder Traversal
void inorder(struct node *root)
if (root! = NULL)
// Traverse left
inorder(root-> left);
// Traverse root
printf("%d -> ", root-> key) ;
// Traverse right
inorder(root-> right);
// Insert a node
struct node *insert(struct node *node, int key)
// Return a new node if the tree is empty
if (node == NULL) return newNode(key) ;
// Traverse to the right place and insert the node
if (key < node-> key)
node-> left = insert(node-> left, key) ;
else
node-> right = insert(node-> right, key) ;
return node;
// Find the inorder successor
struct node *minValueNode(struct node *node)
struct node *current = node;
// Find the leftmost leaf
while (current && current-> left! = NULL)
current = current-> left;
return current;
// Deleting a node
struct node *deleteNode(struct node *root, int key)
// Return if the tree is empty
if (root == NULL) return root;
// Find the node to be deleted
if (key < root-> key)
root-> left = deleteNode(root-> left, key) ;
else if (key > root-> key)
root-> right = deleteNode(root-> right, key) ;
else
// If the node is with only one child or no child
if (root-> left == NULL)
struct node *temp = root-> right;
free(root);
return temp;
else if (root-> right == NULL)
struct node *temp = root-> left;
free(root);
return temp;
// If the node has two children
struct node *temp = minValueNode(root-> right);
// Place the inorder successor in position of the node to be deleted
root-> key = temp-> key;
// Delete the inorder successor
root-> right = deleteNode(root-> right, temp-> key) ;
return root;
// Driver code
int main()
struct node *root = NULL;
root = insert(root, 8);
root = insert(root, 3);
root = insert(root, 1);
root = insert(root, 6);
root = insert(root, 7);
root = insert(root, 10);
root = insert(root, 14);
root = insert(root, 4);
printf("Inorder traversal: ") ;
inorder(root);
printf("\nAfter deleting 10\n") ;
root = deleteNode(root, 10);
printf("Inorder traversal: ") ;
inorder(root);
C++
// Binary Search Tree operations in C++
#include
using namespace std;
struct node
int key;
struct node *left, *right;
};
// Create a node
struct node *newNode(int item) {
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Inorder Traversal
void inorder(struct node *root) {
if (root != NULL) {
// Traverse left
inorder(root->left);
// Traverse root
cout << root->key << " -> ";
// Traverse right
inorder(root->right);
}
}
// Insert a node
struct node *insert(struct node *node, int key) {
// Return a new node if the tree is empty
if (node == NULL) return newNode(key);
// Traverse to the right place and insert the node
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
// Find the inorder successor
struct node *minValueNode(struct node *node) {
struct node *current = node;
// Find the leftmost leaf
while (current && current->left != NULL)
current = current->left;
return current;
}
// Deleting a node
struct node *deleteNode(struct node *root, int key) {
// Return if the tree is empty
if (root == NULL) return root;
// Find the node to be deleted
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else {
// If the node is with only one child or no child
if (root->left == NULL) {
struct node *temp = root->right;
free(root);
return temp;
} else if (root->right == NULL) {
struct node *temp = root->left;
free(root);
return temp;
}
// If the node has two children
struct node *temp = minValueNode(root->right);
// Place the inorder successor in position of the node to be deleted
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}
// Driver code
int main() {
struct node *root = NULL;
root = insert(root, 8);
root = insert(root, 3);
root = insert(root, 1);
root = insert(root, 6);
root = insert(root, 7);
root = insert(root, 10);
root = insert(root, 14);
root = insert(root, 4);
cout << "Inorder traversal: ";
inorder(root);
cout << "\nAfter deleting 10\n";
root = deleteNode(root, 10);
cout << "Inorder traversal: ";
inorder(root);
}
برنامه های درخت جستجوی باینری
- در شاخصسازی چندسطحی در پایگاه دادهپایگاه داده چیست؟ – انواع، مفاهیم و کاربردها
 پایگاه داده چیست؟ این مقاله به بررسی این موضوع و همچنین انواع پایگاه داده، کاربردهای پایگاه داده، محبوب ترین پایگاه های داده و اجزای اصلی پایگاه داده پرداخته
پایگاه داده چیست؟ این مقاله به بررسی این موضوع و همچنین انواع پایگاه داده، کاربردهای پایگاه داده، محبوب ترین پایگاه های داده و اجزای اصلی پایگاه داده پرداخته - برای مرتبسازی پویا
- برای مدیریت مناطق مجازی در هسته یونیکس
جمعبندی
درخت جستجوی دودویی، ساختمان دادهای است که به طور گسترده در علوم کامپیوترعلوم کامپیوتر یا کامپیوتر ساینس چیست در این صفحه به بررسی و موشکافی رشته علوم کامپیوتر اعم از بررسی بازار کار، گرایشها، دروس و چارت درسی این رشته، میزان درآمد و حقوق فارغ التحصیلان این رشته و ادامه تحصیل در این رشته پرداخته شده است. استفاده میشود. آنها اغلب برای ذخیره و بازیابی بهینه دادهها استفاده میشوند و برای جستجو در مجموعهدادههای بزرگ ایدهآل هستند. در این مقاله به معرفی این درختان پرداختیم و برخی عملیات پایه آنها را بررسی کردیم و در نهایت پیچیدگی زمانیپیچیدگی زمانی الگوریتم چیست؟ معرفی نماد های مجانبی
در این صفحه به بررسی و موشکافی رشته علوم کامپیوتر اعم از بررسی بازار کار، گرایشها، دروس و چارت درسی این رشته، میزان درآمد و حقوق فارغ التحصیلان این رشته و ادامه تحصیل در این رشته پرداخته شده است. استفاده میشود. آنها اغلب برای ذخیره و بازیابی بهینه دادهها استفاده میشوند و برای جستجو در مجموعهدادههای بزرگ ایدهآل هستند. در این مقاله به معرفی این درختان پرداختیم و برخی عملیات پایه آنها را بررسی کردیم و در نهایت پیچیدگی زمانیپیچیدگی زمانی الگوریتم چیست؟ معرفی نماد های مجانبی این صفحه عالی به معرفی پیچیدگی زمانی الگوریتم پرداخته، همچنین انواع نماد های مجانبی و پیچیدگی زمانی های برخی از الگوریتم های مرتب سازی و جستجو را توضیح داده و کاربردها و پیادهسازی آنها را دیدیم.
این صفحه عالی به معرفی پیچیدگی زمانی الگوریتم پرداخته، همچنین انواع نماد های مجانبی و پیچیدگی زمانی های برخی از الگوریتم های مرتب سازی و جستجو را توضیح داده و کاربردها و پیادهسازی آنها را دیدیم.
درخت جستجوی دودویی چیست؟
درخت جستجوی دودویی یک الگوریتم پیشرفته برای تجزیهوتحلیل گره و شاخههای چپ و راست آن است که در ساختار درختی مدلسازی شده و مقدار را برمیگرداند. BST بر روی معماری یک الگوریتم جستجوی باینری پایه ابداع شده است؛ ازاینرو جستجو، درج و حذف گرهها بهصورت سریعتر را ممکن میسازد.
مزایای BST چیست؟
BST در درج و حذف در هنگامی که متعادل باشد سریع است (پیچیدگی زمانی O(log n))؛ همچنین BST برای جستجوی سریع، با پیچیدگی زمانی O(log n) برای اکثر عملیات است.
مشکل درختان جستجوی باینری چیست؟
زمان جستجو در BST به ارتفاع (عمق درخت) محدود میشود. هر مرحله در جستجو یک سطح پایین میرود؛ بنابراین در بدترین حالت، باید از ریشه به عمیقترین برگ برویم تا X را پیدا کنیم یا بفهمیم که X در درخت نیست.