برای شروع حرفهای کنکور ارشد کامپیوتر،آیتی و علوم کامپیوتر حتما روی عکس زیر کلیک کنید تا در کانال کنکور کامپیوتر عضو شوید، در این کانال به معرفی بهترین منابع کنکور ارشد،برنامه ریزی و مشاوره، معرفی گرایشها و هر آنچه برای موفقیت در کنکور ارشد نیاز دارید پرداخته شده است

در علوم کامپیوترعلوم کامپیوتر یا کامپیوتر ساینس چیست در این صفحه به بررسی و موشکافی رشته علوم کامپیوتر اعم از بررسی بازار کار، گرایشها، دروس و چارت درسی این رشته، میزان درآمد و حقوق فارغ التحصیلان این رشته و ادامه تحصیل در این رشته پرداخته شده است.، درختان AVL یک ساختمان داده مهم هستند که از درختهای جستجوی باینری خود متعادلکننده استفاده میکنند. هر گره در درخت AVL اطلاعات اضافی به نام ضریب تعادل را در خود دارد که میتواند 1-، 0 یا 1+ باشد. این مقاله به بررسی درختان AVL، عملکرد آنها و ارتباط آنها در الگوریتمالگوریتم چیست به زبان ساده و با مثال های فراوان
در این صفحه به بررسی و موشکافی رشته علوم کامپیوتر اعم از بررسی بازار کار، گرایشها، دروس و چارت درسی این رشته، میزان درآمد و حقوق فارغ التحصیلان این رشته و ادامه تحصیل در این رشته پرداخته شده است.، درختان AVL یک ساختمان داده مهم هستند که از درختهای جستجوی باینری خود متعادلکننده استفاده میکنند. هر گره در درخت AVL اطلاعات اضافی به نام ضریب تعادل را در خود دارد که میتواند 1-، 0 یا 1+ باشد. این مقاله به بررسی درختان AVL، عملکرد آنها و ارتباط آنها در الگوریتمالگوریتم چیست به زبان ساده و با مثال های فراوان در این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد های مرتبسازی و جستجو میپردازد.
در این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد های مرتبسازی و جستجو میپردازد.
عملیات اصلی درختان AVL
برای بررسی عملیات در درختان AVL ابتدا باید مفهوم ضریب تعادل را تعریف کنیم. ضریب تعادل یکی از اجزای حیاتی درخت AVL است. این مفهوم به تفاوت بین ارتفاع زیر درخت چپ و راست یک گره اشاره دارد. فرمول محاسبه ضریب تعادل مطابق زیر است:
ضریب تعادل = (ارتفاع زیر درخت سمت چپ - ارتفاع زیر درخت سمت راست) یا (ارتفاع زیر درخت سمت راست - ارتفاع زیر درخت سمت چپ)
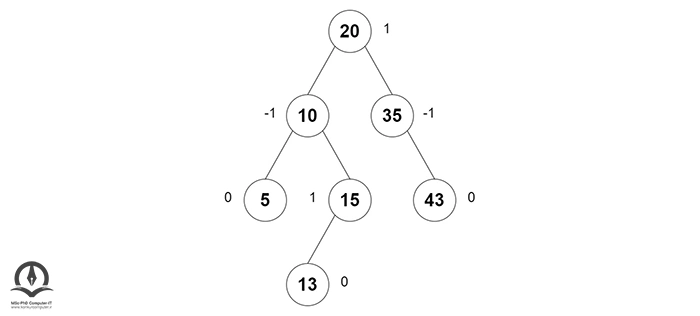
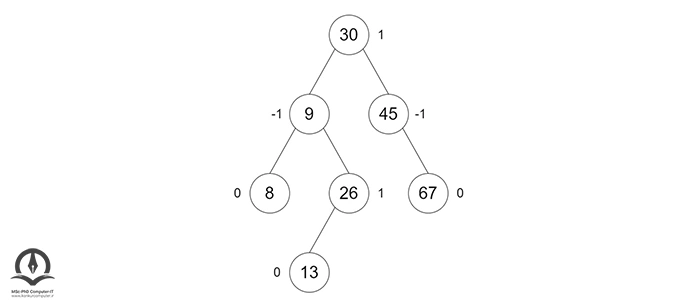
ضریب تعادل همیشه باید 1-، 0 یا 1+ باشد تا اطمینان حاصل شود که درخت AVL خود متعادل باقی میماند. درخت زیر یک مثال برای درخت AVL است:
چرخش در درختان AVL
در عملیات چرخش، موقعیت گرههای یک زیر درخت عوض میشود. سه نوع چرخش وجود دارد:
- چرخش چپ
- چرخش راست
- چرخش چپ - راست و راست - چپ
در ادامه به بررسی هرکدام از این چرخشها میپردازیم.
چرخش چپ
در چرخش چپ، آرایش گرهها در سمت راست به آرایش گره چپ تبدیل میشود. مثال زیر را در نظر بگیرید:
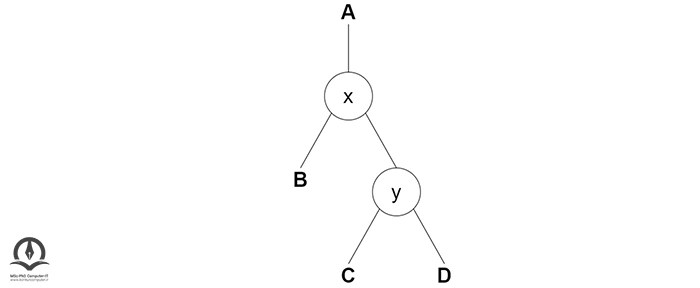
فرض کنید در درخت بالا، x و y هرکدام گره و A، B، C و D هرکدام زیر درخت باشند. مراحل چرخش به چپ در این درخت بهصورت زیر است.
اگر y زیر درخت سمت چپ دارد، x را بهعنوان والد زیر درخت سمت چپ y اختصاص دهید:
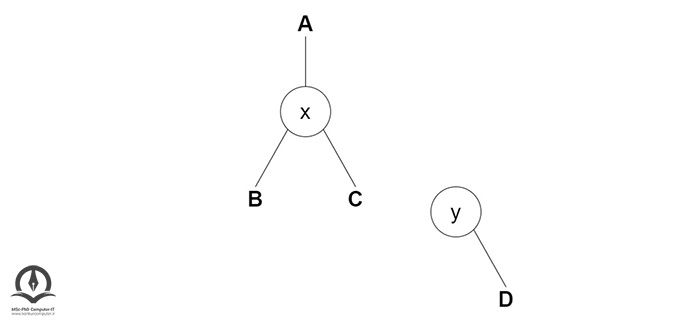
اگر والد x، NULL است، y را ریشه درخت کنید. اگر x فرزند چپ A است، y را فرزند چپ A قرار دهید؛ در غیر این صورت y را بهعنوان فرزند راست A قرار دهید.
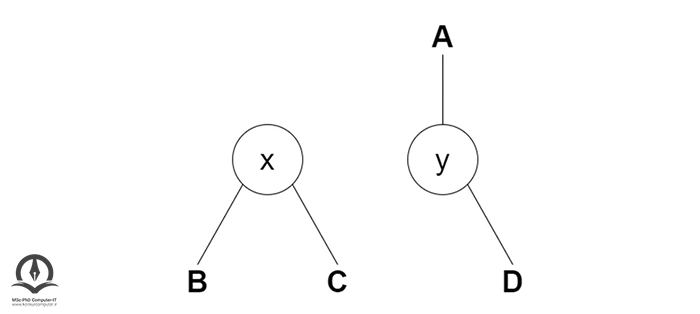
در نهایت y را والد x قرار دهید.
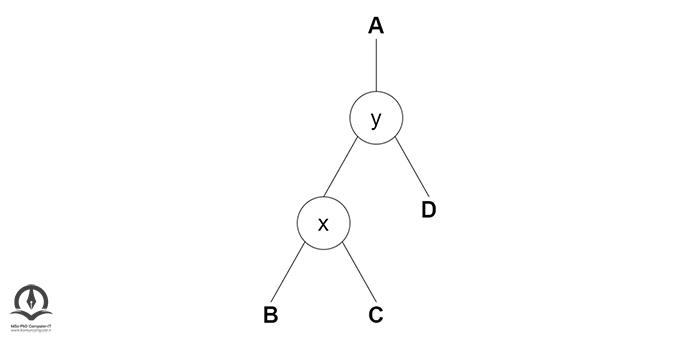
چرخش راست
در چرخش سمت راست، آرایش گرهها در سمت چپ به آرایش گره سمت راست تبدیل میشود. مثال زیر را در نظر بگیرید:
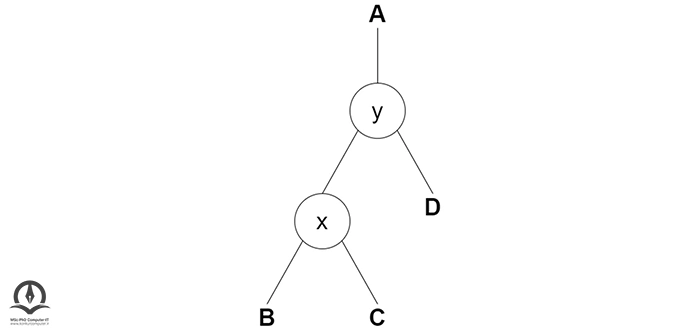
اگر x دارای زیر درخت راست است، y را بهعنوان والد زیر درخت سمت راست x نسبت دهید.
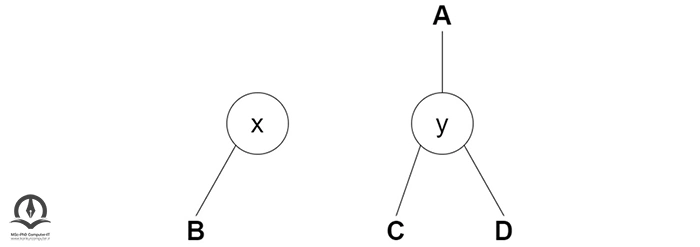
- اگر والد y، NULL است، ریشه درخت را x قرار دهید.
- در غیر این صورت، اگر y فرزند راست والد خود یعنی A است، x را فرزند راست A قرار دهید.
- در غیر این صورت x را بهعنوان فرزند سمت چپ A اختصاص دهید.
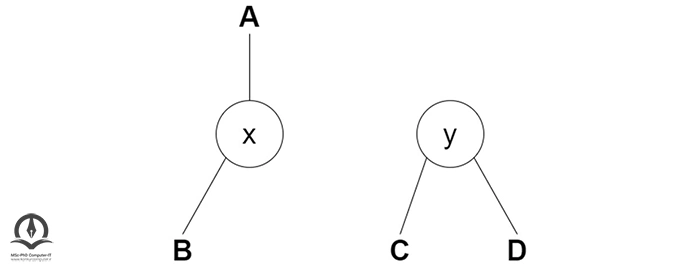
x را والد y کنید:
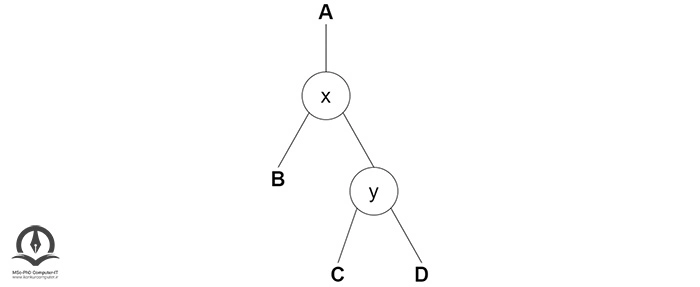
چرخش چپ - راست و راست - چپ
در چرخش چپ - راست، ترتیبها ابتدا به چپ و سپس به راست جابهجا میشوند. مثال زیر را در نظر بگیرید:
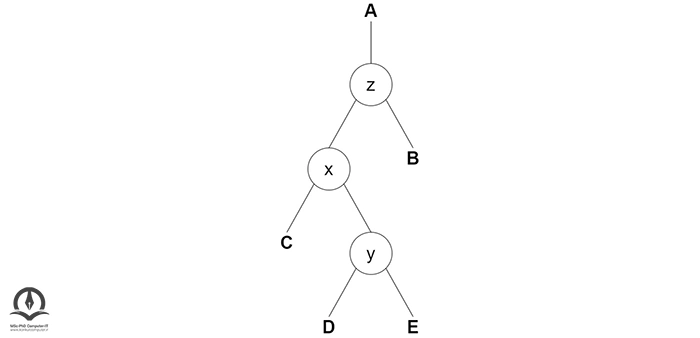
در این درخت ابتدا چرخش بهسمت چپرا روی x-y انجام میدهیم:
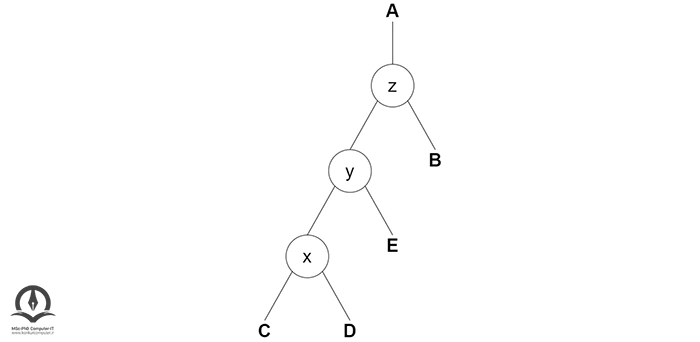
سپس چرخش بهراست را روی y-z انجام میدهیم:
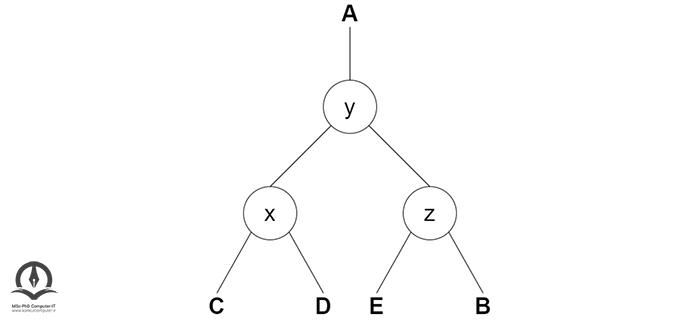
در چرخش راست - چپ، ترتیبها ابتدا به سمت راست و سپس به چپ منتقل میشوند. مثال زیر را در نظر بگیرید:
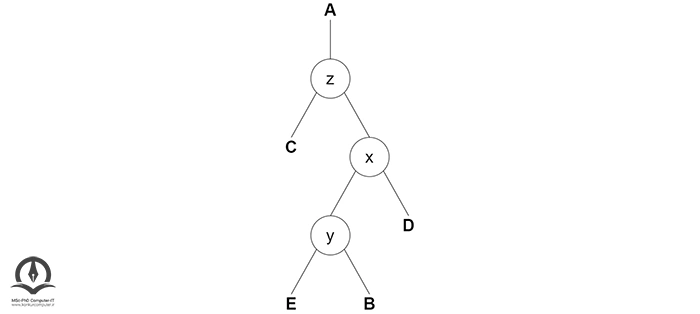
ابتدا چرخش راست را روی x-y انجام میدهیم:
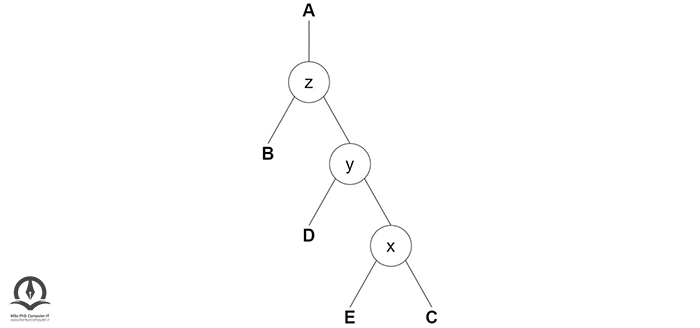
سپس چرخش به چپ را روی z-y انجام میدهیم:
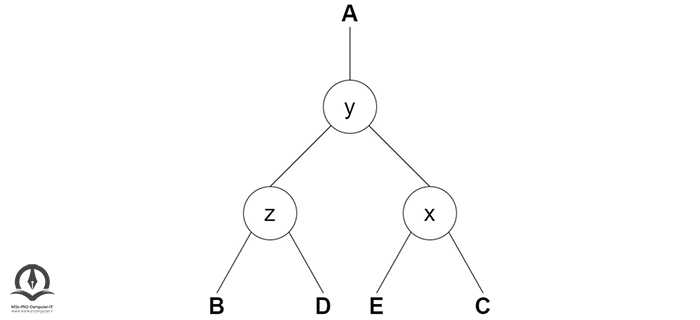
عملیات درج
یک گره جدید همیشه بهعنوان یک گره برگ با ضریب تعادل برابر با 0 درج میشود. مثال زیر را در نظر بگیرید:
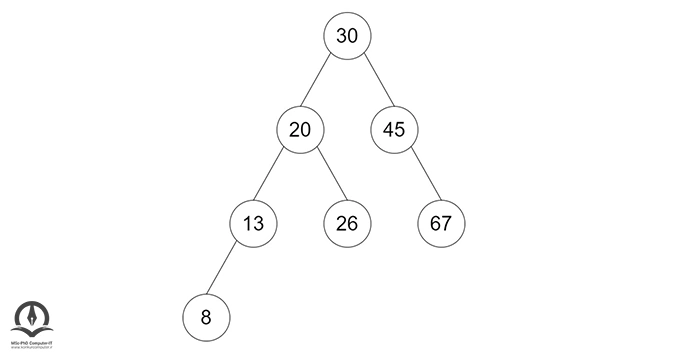
فرض کنید میخواهیم گره 9 را به این درخت اضافه کنیم. برای درج یک گره جدید با استفاده از مراحل بازگشتی زیر، به گره برگ مناسب بروید. کلید جدید را با کلید ریشه درخت فعلی مقایسه کنید.
- اگر کلید جدید کوچکتر از کلید ریشه است، الگوریتم درج را در زیر درخت سمت چپ گره فعلی تا رسیدن به گره برگ فراخوانی کنید.
- در غیر این صورت، اگر کلید جدید بزرگتر از کلید ریشه است، الگوریتم درج را در زیر درخت سمت راست گره فعلی تا رسیدن به گره برگ فراخوانی کنید.
- در غیر این صورت، گره برگ را برگردانید.
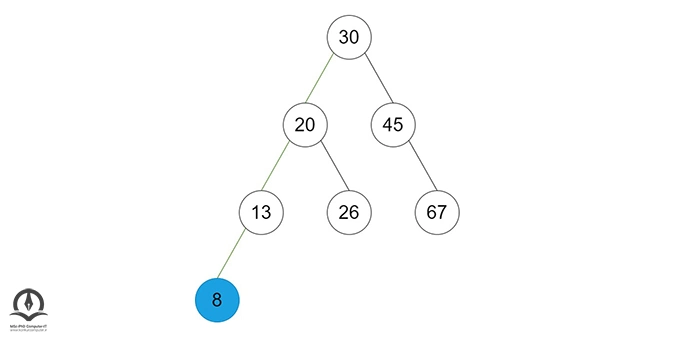
پس از رسیدن به برگ، کلید برگ بهدستآمده از مراحل بالا را با کلید جدید مقایسه کنید:
- اگر کلید جدید کوچکتر از کلید برگ است، گره جدید را بهعنوان فرزند سمت چپ برگ گره ایجاد کنید.
- در غیر این صورت، یک گره جدید بهعنوان فرزند سمت راست گره برگ ایجاد کنید.
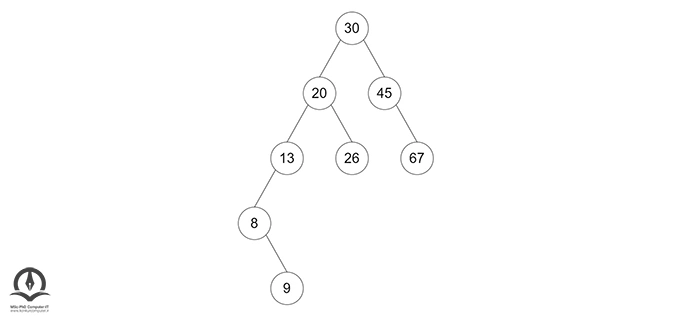
ضریب تعادلهای درخت فعلی به شکل زیر است:
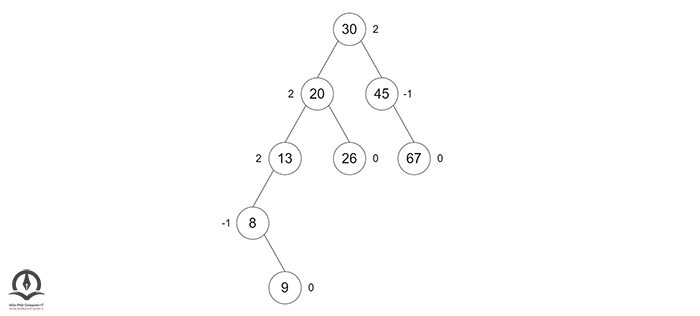
اگر گرهها نامتعادل هستند، گره را باید دوباره متعادل کنید.
- اگر ضریب تعادل > 1 باشد، به این معنی است که ارتفاع زیر درخت سمت چپ بیشتر از ارتفاع زیر درخت سمت راست است؛ بنابراین یک چرخش راست یا چرخش چپ - راست انجام دهید.
- اگر کلید فرزند سمت چپ بزرگتر از کلید گره جدید است، چرخش به راست انجام دهید.
- در غیر این صورت یک چرخش چپ - راست انجام دهید.
- اگر ضریب تعادل < 1- باشد، به این معنی است که ارتفاع زیر درخت سمت راست بیشتر از ارتفاع زیر درخت سمت چپ است؛ بنابراین یک چرخش راست یا چرخش راست - چپ انجام دهید
- اگر کلید فرزند سمت راست کوچکتر از کلید گره جدید است، چرخش به چپ انجام دهید.
- در غیر این صورت یک چرخش راست - چپ انجام دهید.
بر روی درخت فعلی ابتدا یک چرخش چپ انجام میدهیم:
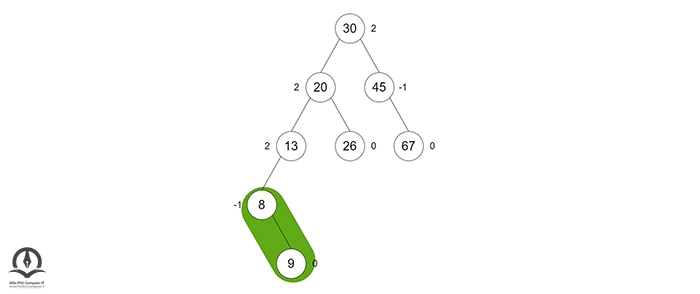
درخت به این شکل درمیآید:
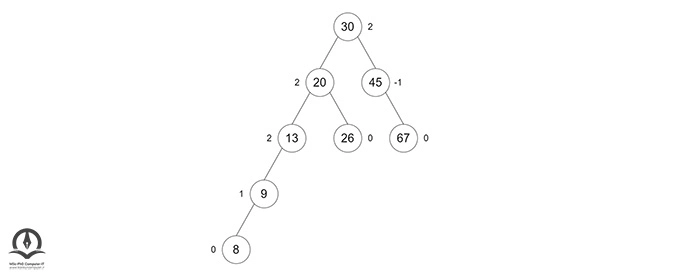
سپس یک چرخش به راست انجام میدهیم:
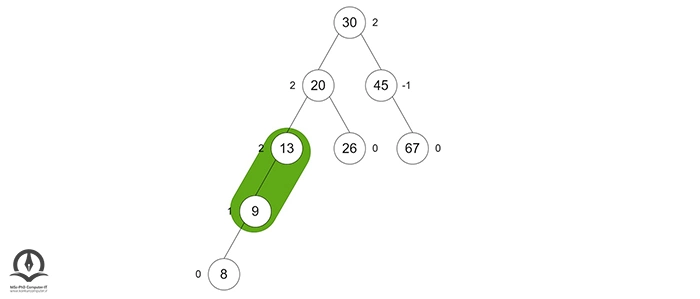
در این مرحله درخت متعادل شده است.
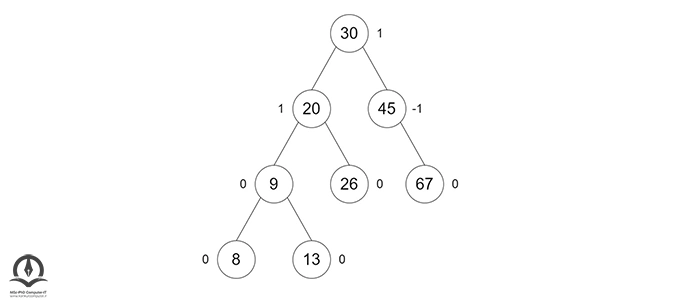
عملیات حذف
یک گره همیشه بهعنوان گره برگ حذف میشود. پسا ز حذف یک گره، عوامل تعادل گرهها تغییر میکند. برای تعادل مجدد ضریب تعادل، چرخشهای مناسب انجام میشوند. برای مثال درخت زیر را در نظر بگیرید:
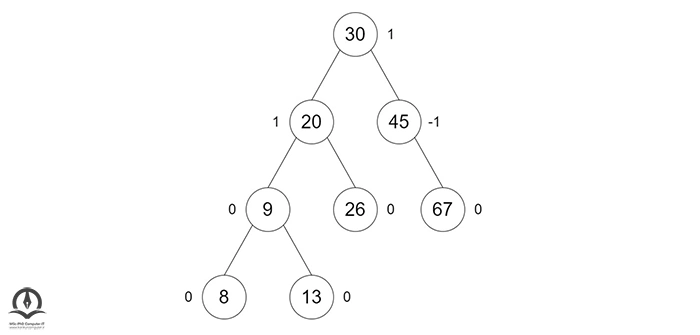
فرض کنید در این درخت میخواهیم گره 20 را حذف کنیم. سه حالت برای حذف یک گره وجود دارد:
- اگر گرهای که باید حذف شود، گره برگ است (فرزندی ندارد)، گرهای که باید حذف شود را حذف کنید.
- اگر گرهای که باید حذف شود دارای یک فرزند است، محتوای گرهای که باید حذف شود را بامحتوای فرزند جایگزین کنید و سپس فرزند را حذف کنید.
- اگر گرهای که باید حذف شود دو فرزند دارد، گره بعدی گرهای که باید حذف شود را در پیمایش Inorder پیدا کنید. (گره با حداقل مقدار کلید در زیر درخت سمت راست)
در این مثال گره 20 دو فرزند دارد و گره بعدی آن در پیمایش Inorder، گره 26 است. مقدار گره 20 را با 26 جایگزین میکنیم و گره 26 را حذف میکنیم:
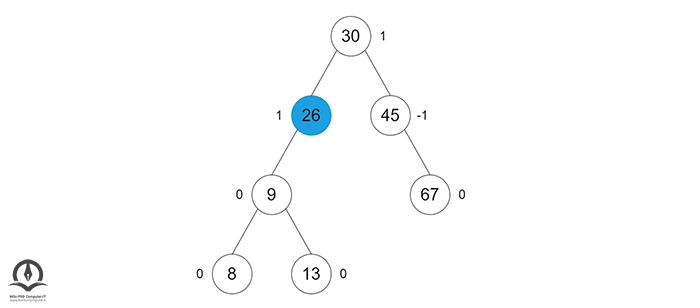
حال ضریب تعادل گرهها را دوباره محاسبه میکنیم:
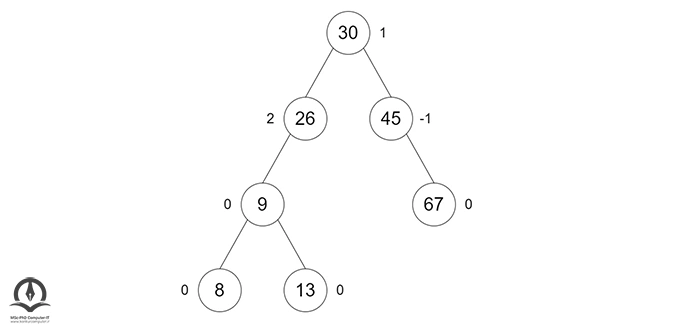
اگر ضریب تعادل هریک از گرهها برابر با 1- ،0 یا 1 نباشد، درخت را مجدداً متعادل کنید.
- اگر فاکتور تعادل گره فعلی > 1 باشد:
- اگر ضریب تعادل فرزند چپ => 0 باشد، چرخش را به راست انجام دهید.
- در غیر این صورت چرخش چپ - راست را انجام دهید.
- اگر ضریب تعادل گره فعلی < 1- باشد،
- اگر ضریب تعادل فرزند راست =< 0 باشد، چرخش به چپ را انجام دهید.
- در غیر این صورت چرخش راست - چپ را انجام دهید.
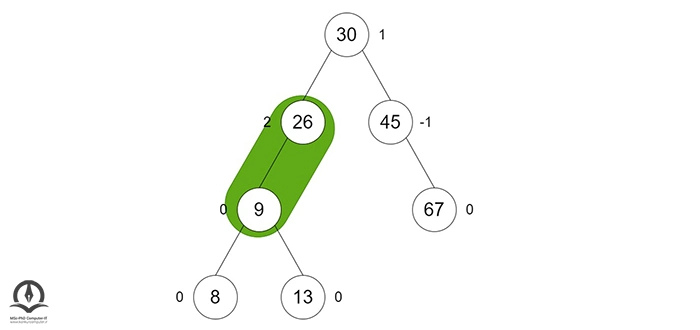
درخت نهایی بهشکل زیر خواهد بود:
پیچیدگی زمانی عملیات های درخت AVL
پیچیدگی زمانیپیچیدگی زمانی الگوریتم چیست؟ معرفی نماد های مجانبی این صفحه عالی به معرفی پیچیدگی زمانی الگوریتم پرداخته، همچنین انواع نماد های مجانبی و پیچیدگی زمانی های برخی از الگوریتم های مرتب سازی و جستجو را توضیح داده هر سه عملیات درج، حذف و جستجو در درخت AVL ازمرتبه O(Log n) است.
این صفحه عالی به معرفی پیچیدگی زمانی الگوریتم پرداخته، همچنین انواع نماد های مجانبی و پیچیدگی زمانی های برخی از الگوریتم های مرتب سازی و جستجو را توضیح داده هر سه عملیات درج، حذف و جستجو در درخت AVL ازمرتبه O(Log n) است.
پیاده سازی درخت AVL
در ادامه به پیادهسازی درخت AVL در زبان های برنامه نویسیزبان های برنامه نویسی چیست؟ این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده مانند پایتونزبان برنامه نویسی پایتون چیست؟ – نحوه شروع و دلایل محبوبیت
این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده مانند پایتونزبان برنامه نویسی پایتون چیست؟ – نحوه شروع و دلایل محبوبیت زبان برنامه نویسی پایتون (Python) چیست؟ این مقاله عالی به بررسی دلایل محبوبیت پایتون، موارد استفاده از پایتون و نحوه شروع به برنامه نویسی پایتون پرداخته و جاواجاوا چیست؟ تعریف، معنی و ویژگی های جاوا (java) از 0تا100
زبان برنامه نویسی پایتون (Python) چیست؟ این مقاله عالی به بررسی دلایل محبوبیت پایتون، موارد استفاده از پایتون و نحوه شروع به برنامه نویسی پایتون پرداخته و جاواجاوا چیست؟ تعریف، معنی و ویژگی های جاوا (java) از 0تا100 جاوا یک زبان برنامه نویسی همه منظوره، مبتنی بر کلاس و شی گرا است که برای داشتن وابستگی های پیاده سازی کمتر طراحی شده است، زبان برنامه نویسی جاوا شبیه ++C است میپردازیم:
جاوا یک زبان برنامه نویسی همه منظوره، مبتنی بر کلاس و شی گرا است که برای داشتن وابستگی های پیاده سازی کمتر طراحی شده است، زبان برنامه نویسی جاوا شبیه ++C است میپردازیم:
Python
# AVL tree implementation in Python
import sys
# Create a tree node
class TreeNode(object):
def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1
class AVLTree(object):
# Function to insert a node
def insert_node(self, root, key):
# Find the correct location and insert the node
if not root:
return TreeNode(key)
elif key < root.key:
root.left = self.insert_node(root.left, key)
else:
root.right = self.insert_node(root.right, key)
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
# Update the balance factor and balance the tree
balanceFactor = self.getBalance(root)
if balanceFactor > 1:
if key < root.left.key:
return self.rightRotate(root)
else:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balanceFactor < -1:
if key > root.right.key:
return self.leftRotate(root)
else:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
# Function to delete a node
def delete_node(self, root, key):
# Find the node to be deleted and remove it
if not root:
return root
elif key < root.key:
root.left = self.delete_node(root.left, key)
elif key > root.key:
root.right = self.delete_node(root.right, key)
else:
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
temp = self.getMinValueNode(root.right)
root.key = temp.key
root.right = self.delete_node(root.right,
temp.key)
if root is None:
return root
# Update the balance factor of nodes
root.height = 1 + max(self.getHeight(root.left),
self.getHeight(root.right))
balanceFactor = self.getBalance(root)
# Balance the tree
if balanceFactor > 1:
if self.getBalance(root.left) >= 0:
return self.rightRotate(root)
else:
root.left = self.leftRotate(root.left)
return self.rightRotate(root)
if balanceFactor < -1:
if self.getBalance(root.right) <= 0:
return self.leftRotate(root)
else:
root.right = self.rightRotate(root.right)
return self.leftRotate(root)
return root
# Function to perform left rotation
def leftRotate(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
# Function to perform right rotation
def rightRotate(self, z):
y = z.left
T3 = y.right
y.right = z
z.left = T3
z.height = 1 + max(self.getHeight(z.left),
self.getHeight(z.right))
y.height = 1 + max(self.getHeight(y.left),
self.getHeight(y.right))
return y
# Get the height of the node
def getHeight(self, root):
if not root:
return 0
return root.height
# Get balance factore of the node
def getBalance(self, root):
if not root:
return 0
return self.getHeight(root.left) - self.getHeight(root.right)
def getMinValueNode(self, root):
if root is None or root.left is None:
return root
return self.getMinValueNode(root.left)
def preOrder(self, root):
if not root:
return
print("{0} ".format(root.key), end="")
self.preOrder(root.left)
self.preOrder(root.right)
# Print the tree
def printHelper(self, currPtr, indent, last):
if currPtr != None:
sys.stdout.write(indent)
if last:
sys.stdout.write("R----")
indent += " "
else:
sys.stdout.write("L----")
indent += "| "
print(currPtr.key)
self.printHelper(currPtr.left, indent, False)
self.printHelper(currPtr.right, indent, True)
myTree = AVLTree()
root = None
nums = [33, 13, 52, 9, 21, 61, 8, 11]
for num in nums:
root = myTree.insert_node(root, num)
myTree.printHelper(root, "", True)
key = 13
root = myTree.delete_node(root, key)
print("After Deletion: ")
myTree.printHelper(root, "", True)
Java
// AVL tree implementation in Java
// Create node
class Node {
int item, height;
Node left, right;
Node(int d) {
item = d;
height = 1;
}
}
// Tree class
class AVLTree {
Node root;
int height(Node N) {
if (N == null)
return 0;
return N.height;
}
int max(int a, int b) {
return (a > b) ? a : b;
}
Node rightRotate(Node y) {
Node x = y.left;
Node T2 = x.right;
x.right = y;
y.left = T2;
y.height = max(height(y.left), height(y.right)) + 1;
x.height = max(height(x.left), height(x.right)) + 1;
return x;
}
Node leftRotate(Node x) {
Node y = x.right;
Node T2 = y.left;
y.left = x;
x.right = T2;
x.height = max(height(x.left), height(x.right)) + 1;
y.height = max(height(y.left), height(y.right)) + 1;
return y;
}
// Get balance factor of a node
int getBalanceFactor(Node N) {
if (N == null)
return 0;
return height(N.left) – height(N.right);
}
// Insert a node
Node insertNode(Node node, int item) {
// Find the position and insert the node
if (node == null)
return (new Node(item));
if (item node.item)
node.right = insertNode(node.right, item);
else
return node;
// Update the balance factor of each node
// And, balance the tree
node.height = 1 + max(height(node.left), height(node.right));
int balanceFactor = getBalanceFactor(node);
if (balanceFactor > 1) {
if (item node.right.item) {
return leftRotate(node);
} else if (item < node.right.item) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
}
return node;
}
Node nodeWithMimumValue(Node node) {
Node current = node;
while (current.left != null)
current = current.left;
return current;
}
// Delete a node
Node deleteNode(Node root, int item) {
// Find the node to be deleted and remove it
if (root == null)
return root;
if (item root.item)
root.right = deleteNode(root.right, item);
else {
if ((root.left == null) || (root.right == null)) {
Node temp = null;
if (temp == root.left)
temp = root.right;
else
temp = root.left;
if (temp == null) {
temp = root;
root = null;
} else
root = temp;
} else {
Node temp = nodeWithMimumValue(root.right);
root.item = temp.item;
root.right = deleteNode(root.right, temp.item);
}
}
if (root == null)
return root;
// Update the balance factor of each node and balance the tree
root.height = max(height(root.left), height(root.right)) + 1;
int balanceFactor = getBalanceFactor(root);
if (balanceFactor > 1) {
if (getBalanceFactor(root.left) >= 0) {
return rightRotate(root);
} else {
root.left = leftRotate(root.left);
return rightRotate(root);
}
}
if (balanceFactor < -1) {
if (getBalanceFactor(root.right) = 0) {
return leftRotate(root);
} else {
root.right = rightRotate(root.right);
return leftRotate(root);
}
}
return root;
}
void preOrder(Node node) {
if (node != null) {
System.out.print(node.item + “ “);
preOrder(node.left);
preOrder(node.right);
}
}
// Print the tree
private void printTree(Node currPtr, String indent, boolean last) {
if (currPtr != null) {
System.out.print(indent);
if (last) {
System.out.print(“R----");
indent += “ “;
} else {
System.out.print(“L----");
indent += “| “;
}
System.out.println(currPtr.item);
printTree(currPtr.left, indent, false);
printTree(currPtr.right, indent, true);
}
}
// Driver code
public static void main(String[] args) {
AVLTree tree = new AVLTree();
tree.root = tree.insertNode(tree.root, 33);
tree.root = tree.insertNode(tree.root, 13);
tree.root = tree.insertNode(tree.root, 53);
tree.root = tree.insertNode(tree.root, 9);
tree.root = tree.insertNode(tree.root, 21);
tree.root = tree.insertNode(tree.root, 61);
tree.root = tree.insertNode(tree.root, 8);
tree.root = tree.insertNode(tree.root, 11);
tree.printTree(tree.root, “”, true);
tree.root = tree.deleteNode(tree.root, 13);
System.out.println(“After Deletion: “);
tree.printTree(tree.root, “”, true);
}
}
کاربردهای درخت AVL
کاربردهای درخت AVL شامل موارد زیر است:
- برای شاخصسازی رکوردهای عظیم در پایگاه دادهپایگاه داده چیست؟ – انواع، مفاهیم و کاربردها
 پایگاه داده چیست؟ این مقاله به بررسی این موضوع و همچنین انواع پایگاه داده، کاربردهای پایگاه داده، محبوب ترین پایگاه های داده و اجزای اصلی پایگاه داده پرداخته
پایگاه داده چیست؟ این مقاله به بررسی این موضوع و همچنین انواع پایگاه داده، کاربردهای پایگاه داده، محبوب ترین پایگاه های داده و اجزای اصلی پایگاه داده پرداخته - برای جستجو در پایگاهدادههای بزرگ
جمعبندی
درختان AVL یک ساختمان داده حیاتی برای ذخیرهسازی و بازیابی بهینه اطلاعات در علوم کامپیوتر هستند. این درختان خود متعادل کننده هستند و امکان جستجوی سریع، عملیات درج/حذف و سازگاری را فراهم میکنند. در این مقاله به مفهوم درختان AVL، یک ساختمان داده درخت جستجوی باینری متعادل که معمولاً در علوم کامپیوتر استفاده میشود پرداختیم؛ همچنین به بررسی عملیات اساسی این نوع درختان پرداختیم و به پیادهسازی آنها اشاره کردیم.
تفاوت بین درخت جستجوی باینری و درخت AVL چیست؟
در درخت جستجوی باینری، درج و حذف آسان است؛ زیرا نیازی به چرخش نیست. در درخت AVL، درج و حذف پیچیده هستند و به فرایندهای متعددی برای متعادلکردن درخت نیاز دارند.
چرا AVL بهتر از BST است؟
درخت AVL همیشه با ارتفاع متعادل است و ارتفاع آن همیشه O(Log n) است که در آن n تعداد کل گرههای درخت است. پیچیدگیهای زمانی همه عملیات در AVL بهتراز BST است؛ زیرا بدترین پیچیدگی زمانی درخت AVL در تمام عملیات بهصورت O(Log n) است، درحالیکه در BST، بدترین حالت از مرتبه O(n) است.
در چه مواردی از درخت AVL استفاده میشود؟
از آن برای نمایهسازی رکوردهای عظیم در پایگاه داده و همچنین جستجوی مؤثر در آن استفاده میشود. درختان AVL برای همه انواع مجموعههای درون حافظه ازجمله مجموعهها و دیکشنریها استفاده میشوند. کاربرد دیگر این درختان، برنامههای کاربردی پایگاه داده است، جایی که درج و حذف کمتر رایج است؛ اما جستجوی مکرر دادهها متداول است.
پیچیدگی زمانی درخت AVL چقدر است؟
همانطور که از ارتفاع درخت AVL عبور میکنیم، در این مورد، پیچیدگی زمانی O(Log n) خواهد بود. بدترین حالت زمانی است که درخت پس از اضافهکردن گره جدید از تعادل خارج میشود و چرخش لازم است. پیچیدگی زمانی در این مورد نیز O (Log n) است.