درس مدار منطقی یکی از دروس ضروری رشته مهندسی کامپیوتر می‌باشد، از این جهت که نحوه عملکرد مدارات مجتمع که مبنای کامپیوترها می‌باشد را تشکیل می‌دهد. در درس مدار منطقی به مدارهای ترکیبی و ترتیبی اشاره میشود، نحوه طراحی این مدارها بیان میشود و…. بنابراین مهم نیست که در چه گرایشی در مقطع ارشد نیز می‌خواهید تحصیل کنید، دانش مدارهای منطقی یا سیستمهای دیجیتال برای شما ضروری است. در ادامه این مقاله، پس از معرفی درس مدار منطقی، به تحلیل درس مدار منطقی توسط دکتر رضوی خواهیم پرداخت، بهترین منبع درس مدار منطقی را معرفی خواهیم کرد، سرفصل و مراجع درس مدار منطقی را بیان می‌کنیم و…. بنابراین ادامه مقاله را از دست ندهید.
فیلم های رایگان آموزش مدار منطقی که به آنها نیاز دارید
در حال حاضر فیلم آموزش مدار منطقی استاد رضوی پرطرفدارترین و پرفروش‌ترین فیلم آموزشی مدار منطقی کشور است و هر سال اکثر دانشجویان کامپیوتر کشور این فیلم را تهیه میکنند. اگر می‌خواهید از کیفیت تدریس درس مدار های منطقی توسط استاد رضوی آگاه شوید، در زیر شش جلسه اول دوره درس مدار منطقی، سه جلسه اول دوره نکته و تست مدار منطقی و حل تستهای کنکور ارشد کامپیوتر سال‌های ۹۷ و ۹۸ و ۹۹ و 1402 و 1403 برای درس مدار منطقی که توسط دکتر رضوی تدریس شده است، به صورت کاملاً رایگان آورده شده است و شما با مشاهده آن میتوانید به کیفیت و جامعیت این دوره پی ببرید. توصیه می‌کنیم حتماً این ویدئو‌ها را مشاهده کنید.
در فیلم زیر به تحلیل و بررسی درس مدار منطقی پرداختیم، در این فیلم توضیح داده شده که فیلم درس مدار منطقی برای چه افرادی مناسب است و همین طور در خصوص فصول مختلف درس مدار منطقی و اهمیت هر کدام از فصول آن صحبت شده است.
مدار منطقی چیست
دنیای باینری (صفر و یک) امروزی به ما کمک کرده تا از جهان فیزیکی و همه شگفتی‌های آن نقشه برداری کنیم و به روند پیشرفت فناوری و تکنولوژی سرعت ببخشیم. بعنوان مثال امروزه میتوان بسته‌هایی را در عرض چند دقیقه با استفاده از هواپیماهای بدون سرنشین به صاحبشان تحویل داد. اما برای عبور از دنیای صفر و یکی و رسیدن به آخرین پیشرفت‌های فناوری باید از گیت‌های منطقی (Logic Gate) عبور کنیم.
مدار منطقیآموزش مدار منطقی
در حال حاضر فیلم آموزش مدار منطقی استاد رضوی پرطرفدارترین و پرفروش‌ترین فیلم اموزشی مدار منطقی کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند، آموزش مدار منطقی به زبان ساده و صفر تا صد دلیل محبوبیت آموزش منطقی است (به انگلیسی Logic Circuit)، مدارات الکتریکی هستند که خروجی آنها به ورودی وابسته بوده، به نحوی که میتوان آن را به صورت تابعی در منطق نمادین بیان کرد.برای کنترل جریان در یک مدار الکتریکی از دروازه یا گیتی به نام ترانزیستورها استفاده میشود که هرکدام از این ترانزیستورها می‌توانند در یکی از دو حالت روشن یا خاموش (باز یا بسته) قرار بگیرند. زمانی که یک ترانزیستور روشن است؛ ولتاژی در حدود 5 ولت از آن عبور کرده و منطق یک را بوجود می‌آورد و وقتی در حالت خاموش قرار دارد، جریان عبوری از آن برابر صفر ولت خواهد بود و بیان‌کننده منطق صفر است.
مدارات منطقی را میتوان از هر وسیله الکتریکی یا الکترونیکی باینری از جمله سوئیچ‌ها، رله‌ها، لوله‌های الکترونی، دیودهای حالت جامد و ترانزیستورها ساخت. انتخاب هر یک از این روش‌ها بستگی به کاربرد و الزامات طراحی دارد.
خرید فیلم های کامل مدار منطقی
در زیر بهترین منابع برای درس مدارهای منطقی معرفی آورده شده‌اند و برای کسب اطلاعات کامل‌تر و تهیه آنها میتوانید به لینک هر یک از آنها مراجعه کنید. توجه داشته باشید که دو دوره درس مدار منطقی و دوره نکته و تست در مدار منطقی مکمل یکدیگر می‌باشند. در دوره درس مدار منطقی، تدریس به صورتی است که نیاز به دانش قبل ندارد. همچنین در دوره نکته و تست مدار منطقی نیز به تمامی تستهای درس مدار منطقی اشاره شده است. شما با تهیه این منابع، نیاز به هیچ منبع و کتاب دیگری ندارید.
ویدیو درس مدار منطقی
تخفیف زمانی تا ۲۵ تیر
30%ویدیو نکته و تست مدار منطقی
تخفیف زمانی تا ۲۵ تیر
30%معرفی مدار منطقی
وقتی دسته‌ای از این ترانزیستورها را به هم متصل می‌کنید، چیزی به نام گیت منطقی دریافت می‌کنید که به شما امکان می‌دهد اعداد باینری را به هر شکلی ، جمع، تفریق، ضرب و تقسیم کنید. گیت‌های AND ،OR و NOT از مهمترین گیت‌های منطقی محسوب می‌شوند.
امروزه درک صحیحی از مدارهای منطقی برای هر مهندس برق و کامپیوتر ضروری است. این مدارها عنصر اصلی کامپیوترها و بسیاری از وسایل دیگر نظیر: دستگاه‌های ضبط و پخش موسیقی و تصویر، بازی‌های الکترونیک، ساعت‌های دیجیتال، دوربین‌های فیلمبرداری، گیرنده‌های تلویزیون، چاپگرها و بسیاری از لوازم خانگی و همچنین در سیستمهای بزرگ مانند شبکه‌های تلفن، تجهیزات اینترنت، ایستگاه‌های پخش رادیویی و تلویزیونی، کارخانه‌های صنعتی و تجهیزات پزشکی. هستند. مشخص است که مدارهای منطقی یکی از اجزای بسیار مهم در زندگی امروزی ما محسوب می‌شوند.
هدف درس مدار منطقی آشنا کردن شما با فرایند طراحی مدارهای منطقی است. روند آموزش در درس مدار منطقی به اینصورت است که ابتدا ایده‌های کلیدی و عناصر پایه‌ی مدارهای منطقی با مثال‌های ساده تشریح میشود، سپس آموزش داده میشود که چگونه میتوان با این عناصر پایه مدارهای بسیار پیچیده خلق کرد.
مدار منطقی چیست و هر یک از گیت‌ها در مدار منطقی چگونه عمل میکنند؟
درس مدار منطقی
درس مدار منطقی جزو یکی از دروس مهم و اصلی مهندسی کامپیوتر و مهندسی برق است که به طور معمول در ترم 3 مقطع کارشناسی گذرانده میشود. اهمیت درس مدار منطقی تا جاییست که بعنوان یکی از منابع کنکور ارشد مهندسی کامپیوتر نیز بشمار می‌آید. تجزیه و تحیل ساختار مدارهای منطقی و آشنایی با ساز و کار آنها از مباحث اصلی این درس محسوب می‌شوند که با گذاشتن کمی وقت و مطالعه دقیق مباحث میتوانید به خوبی بر این درس مسلط شوید.
درس مدار منطقی پیش‌نیاز چه درسهایی در دانشگاه است؟
براساس چارت درسی ارائه شده توسط دانشگاه صنعتی شریف، درس مدار منطقی پیش‌نیاز دو درس آزمایشگاه‌های مدار منطقی (یک واحدی) و ساختار و زبان کامپیوتر (3 واحدی) است. که باز درس ساختار و زبان کامپیوتر نیز پیش‌نیاز درس معماری کامپیوتر به حساب می آید که جزو یکی از دروس مهم و اصلی رشته کامپیوتر در مقطع لیسانس به شمار می‌آید.
درس مدار منطقی چه پیش‌نیازهایی در دانشگاه دارد؟
در چارت درسی بعضی از دانشگاههای دولتی مانند دانشگاه شریف، تهران و امیرکبیر درس مدار منطقی دارای هیچ پیش نیازی نیست و در بازه زمانی تعیین شده میتوان این درس را اخذ نمود. اما در برخی دیگر از دانشگاه‌ها مانند دانشگاه آزاد اسلامی، اخذ این درس منوط به گذراندن دروسی مانند ریاضیات گسسته و ریاضی عمومی 1 و 2 است که در صورت قبولی در آنها میتوانید درس مدار منطقی را بگذرانید.
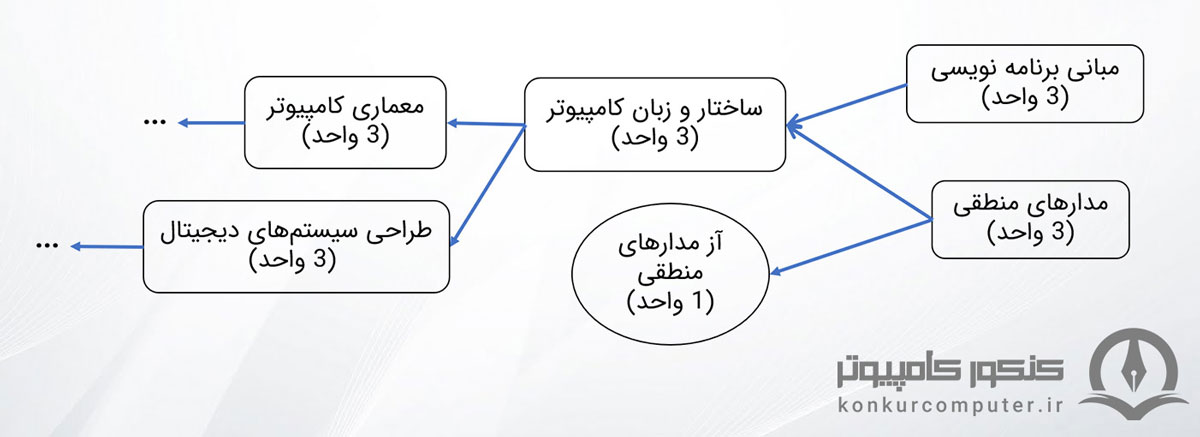
فصل‌های مدار منطقی
رئوس مطالبی که در درس مدار منطقی وجود دارد عبارت است از: اعداد و سیستمهای مختلف اعداد، جبر بول، ساده سازی، ایجاب کننده و PI و EPI، مخاطره و هازارد، مدارات ترکیبی، تحلیل مدارات ترتیبی، طراحی مدارات ترتیبی، کاهش حالات. برای مشاهده اهمیت هر فصل و اینکه در سال‌های اخیر از هر فصل درس مدار منطقی چه تعداد تست مطرح شده به قسمت بودجه‌بندی سوالات کنکور ارشد مهندسی کامپیوتر مراجعه کنید.
- کاربرد سیستمهای دیجیتال در دنیای کنونی
- مبانی سیستمهای دیجیتال و تفاوت آنها با سیستمهای آنالوگ
- معرفی اجمالی مدارهای دیجیتال بر پایه ترانزیستورهای MOS
- محاسبات در سیستمهای دیجیتال
- مفاهیم Carry و Overflow
- سیستمهای نمایش BCD
- توابع، عملگرها و گیت‌های منطقی
- روابط جبر بول
- نمایش Minterm، Maxterm و فرم‌های استاندارد نمایش توابع منطقی
- آموزش زبان توصیف سخت افزار (VHDL یا Verilog) در سطح ساختاری
- بهینه سازی مدارهای ترکیبی با جدول کارنو و الگوریتم کوئین مک کلاسکی و مفهوم حالات بی اهمیت (Do not care)
- مفهوم Race و Hazard و Glitch
- انواع پیاده سازی مدارهای دو طبقه
- مفهوم تاخیر
- مدارهای کدگذار، کدگشا، تسهیم کننده، پاد تسهیم کننده
- طراحی با گیت‌های جهانی (Universal)
- مدارهای جمع کننده انتشاری، مقایسه کننده، جمع کننده با پیش بینی رقم نقلی
- مفهوم امپدانس بالا و استفاده از بافرهای سه حالته برای ایجاد امپدانس بالا، مدار با گیت‌های کلکتور باز، منطق سیمی، استفاده از مقاومت به عنوان Pull-up و Pull-down
- مدارهای برنامه پذیر (PAL,PLA,ROM,FPGA)
- معرفی تراشه‌های استاندارد ترکیبی
- تاخیر انتشار عناصر حافظه، مفهوم زمان راه اندازی (Setup Time) و زمان نگهداشت (Hold Time)، ورودی‌های همگام و ناهمگام
- تحلیل مدارهای ترتیبی، جدول تحریک، نمودار حالت، جدول حالت
- مراحل طراحی FSM، مدل‌های Mealy و Moor و تفاوت آنها
- طراحی مدارهای ترتیبی با انواع فلیپ فلاپ‌ها
- شمارنده‌ها، ثبات‌ها و شیفت دهنده‌ها و ثبات‌های Universal
- معرفی تراشه‌های استاندارد ترتیبی
برای آگاهی دقیق‌تر از سرفصل در مدار منطقی، میتوانید به صفحه سرفصل درس مدار منطقی مراجعه کنید.
مراجع درس مدار منطقی
مرجع اصلی که برای درس مدار منطقی در دانشگاههای معتبر تدریس میشود کتابهای مانو و نلسون است، همچنین کتابهای هریس (Harris) و براون (Brown) نیز در برخی از دانشگاههای ایران و جهان تدریس میشود، در زیر کتاب های مرجع مدار منطقی را برای شما عزیزان قرار داده ایم تا براحتی بتوانید آنها را دانلود و از آنها استفاده کنید.
برای دانلود سایر کتاب های مرجع رشته کامپیوتر به قسمت دانلود کتابهای زبان اصلی رشته کامپیوتر و فناوری اطلاعات مراجعه کنید. البته خواندن کتابهای مرجع را به دانشجویان ترم‌های پایین‌تر توصیه می‌کنم نه به دانشجویانی که قصد شرکت در کنکور اشد و دکتری کامپیوتر را دارند، دلیل این امر نیز در قسمت سوالات متداول چندین بار بیان شده است که میتوانید به آن قسمت رجوع کنید. دانشجویانی که قصد دارند برای کنکور ارشد و یا دکتری کامپیوتر این درس مهم را بخوانند، می‌توانند از منابعی که در قسمت معرفی منابع ارشد کامپیوتر معرفی شده استفاده کنند.
کتاب های مدار منطقی
گیت های منطقی
هر گیت منطقی یک عمل بسیار ساده را انجام می‌دهد، و برای ایجاد عملکردهای پیچیده‌تر باید تعداد زیادی گیت منطقی را با آرایشی خاص به یکدیگر متصل کنیم. گیت‌های منطقی از ترانزیستور ساخته شده‌اند، که خود این ترانزیستورها نیز به کمک لایه‌های متعدد از مواد خاص روی یک قرص سیلیکون کاشته می‌شوند.
گیت AND
یک گیت AND می‌تواند دو یا چند ورودی و تنها یک خروجی داشته باشد. تصویر زیر نماد یک مدار AND و جدول بیانگر ترکیبات منطقی گیت است. (در تصویر نماد گیت، پایانه های ورودی در سمت چپ و پایانه خروجی در سمت راست قرار دارند). تنها زمانی خروجی گیت AND، یک خواهد شد که همه ورودی ها یک باشند.
| جدول درستی گیت AND | ||
|---|---|---|
| Q | B | A |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
گیت OR
این گیت مطابق با حالت منطقی کلمه "یا" رفتار می‌کند و برای اینکه عدد یک در خروجی ظاهر شود، باید مقدار حداقل یکی از ورودی‌ها برابر یک باشد. در گیت OR، ورودی‌ها به یکدیگر وابسته نیستند و تا زمانی که یکی از آنها وجود داشته باشد، گیت نیز در حالت روشن قرار خواهد داشت. همه مقادیر ممکن برای دو ورودی A و B در جدول درستی زیر با خروجی Q نشان داده شده است.
| جدول درستی گیت OR | ||
|---|---|---|
| Q | B | A |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
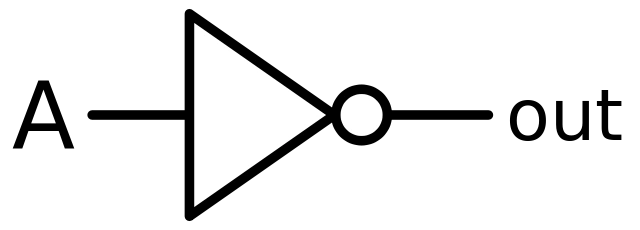
گیت NOT
گیت NOT در مقایسه با سایر گیت‌ها کمی عجیب به نظر میرسد، زیرا همیشه برعکس مقدار ورودی که می‌گیرد، عمل می کند. این گیت ها برای تولید خروجی خود تنها به یک ورودی نیاز دارند، در حالی که سایر گیت ها نیازمند حداقل دو ورودی هستند. جدول درستی زیر خروجی (Q) یک گیت NOT را با تنها یک ورودی (A) نمایش می‌دهد.
| جدول درستی گیت NOT | ||
|---|---|---|
| Q | A | |
| 1 | 0 | |
| 0 | 1 | |
گیت XOR
یک گیت XOR دقیقاً مانند گیت OR عمل می‌کند، با این تفاوت که اگر هر دو ورودی ما وجود داشته باشند مقدار خروجی صفر خواهد بود. یا به عبارتی دیگر اگر شما در ورودی ترکیبی از اعداد صفر و یک داشته باشید خروجی شما همیشه برابر یک خواهد بود، و اگر دو ورودی مشابه داشته باشید (هردو صفر یا هردو یک باشند) عدد صفر را بعنوان خروجی دریافت خواهید کرد. در جدول درستی زیر میتوانید همین مقادیر را مشاهده نمایید.
| جدول درستی گیت XOR | ||
|---|---|---|
| Q | B | A |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
با قراردادن یک گیت NOT بر سر خروجی هریک از گیت‌های AND، OR و XOR می توانید معکوس خروجی‌های هرکدام را داشته باشید. حالت معکوس هریک از این گیت‌ها به صورت نمایشی در تصاویر زیر نشان داده شده است.
گیت NOR
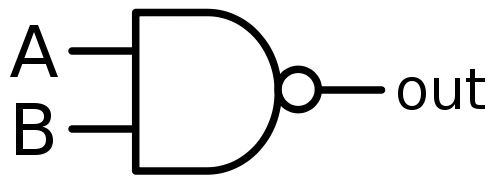
گیت NAND
گیت XNOR
پیاده سازی گیت های منطقی با ترانزیسوتر
در فیلم زیر توضیح داده شده است که چرا در سیستمهای کامپیوتری از دو مقدار 0 و 1 یعنی باینری استفاده می‌کنیم، همین طور در خصوص نحوه تولید و ساخت گیت‌های منطقی معروف OR و AND و NOT توضیح داده شده است.
رسم مدار منطقی
اولین قدم برای رسم یک مدار منطقی این است که با اشکال قراردادی هر یک از گیت‌های منطقی مانند AND، OR و ... آشنا باشید، که در بخش گیت‌های منطقی، اشکال هر یک از این گیت‌ها معرفی شدند.
بطور کلی برای هر تابع یا عبارت جبری میتوان مدار منطقی متناظر با آن را ترسیم کرد. برای رسم مدار، از سمت چپ عبارت جبری شروع کرده و متناسب با تابع بولی، گیت‌های متناظر را به یکدیگر وصل و خروجی مورد نظر را تولید می‌کنیم. لطفا به مثال های مدار منطقی زیر توجه کنید:
F(a,b,c) = (A.B) + C
گام اول: ورودی A و B را به گیت AND وارد می‌کنیم.
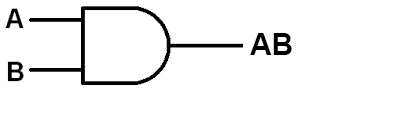
گام دوم: خروجی AB و ورودی C را وارد گیت OR می‌کنیم.
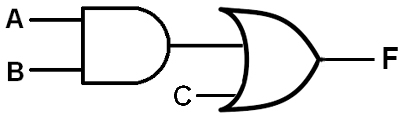
در نهایت مقدار تابع F در خروجی تولید می شود.
با افزایش تعداد ورودی‌ها و گیت‌های منطقی در یک تابع، تعداد طبقات و یا عمق مدار منطقی نیز بیشتر شده و در نهایت مدار پیچیده‌تری خواهیم داشت. علاوه بر این گیت‌های منطقی برای اعمال تغییرات بر روی ورودی‌ها و تولید خروجی مورد انتظار دارای یک تاخیر زمانی هستند و با افزایش تعداد گیت‌ها در مدار منطقی، تاخیر مدار نیز بیشتر خواهد شد. به همین منظور برای کاهش سطوح در مدار منطقی و سریع‌تر کردن آن از روش‌های ساده سازی استفاده میکنند. روش‌های ساده سازی می‌توانند سطوح مدار را تا سطح دوم کاهش داده و مدار را تا حد امکان ساده و سریع کنند.
روش جدول کارنو، کوئین مک کلاسکی و قوانین جبر بول از روش‌های ساده سازی یک تابع بولی هستند.
گیت کامل
هر مداری را میتوانید با داشتن سه گیت AND، OR و NOT بکشید (پیاده سازی کنید)، به همین علت مجموعه این سه گیت را کامل می‌گویند و می‌گویند مجموعه گیت {AND، OR ، NOT} کامل است.
ما مجموعه های دیگری از گیت‌ها را نیز داریم که کامل هستند، حتی ممکن است یک گیت به تنهایی کامل باشد، هر مجموعه‌ای از گیت‌ها یا هر گیت اگر قرار است کامل باشد باید بتواند سه گیت AND، OR و NOT را بسازد.
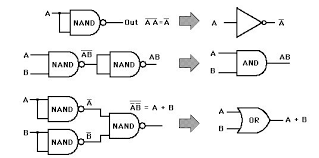
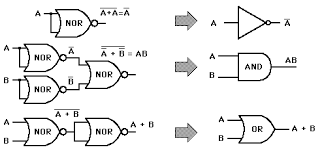
بعنوان مثال گیت NAND به تنهایی کامل است، چون همانطور که در شکل زیر میبینید فقط با استفاده از همین گیت می‌توانیم گیت‌های AND، OR و NOT را بسازیم. گیت NOR نیز یک گیت کامل است، چرا که این گیت‌ها می‌توانند هر سه تابع پایه AND، OR و NOT را تولید کنند.
در تصاویر زیر میتوانید طریقه ساختن هر یک از گیت‌های پایه (AND، OR و NOT) را توسط هر یک از گیت‌های NAND و NOR مشاهده نمایید.
شکل الف : رسم توابع پایه با گیت NAND
شکل ب : رسم توابع پایه با گیت NOR
رسم مدار منطقی تمام NAND یا تمام NOR
یکی از روش‌هایی که بر روی مدارهای دوسطحی اعمال میشود، تمام NAND و یا تمام NOR کردن آنهاست. چرا که در اکثر مدارهای مجتمع یا IC از گیت‌های NAND و NOR استفاده میشود و پیاده‌سازی منطق‌های NAND و NOR از دیدگاه عملی جایگاه ویژه‌ای در طراحی و ساخت مدارهای منطقی دارند. در این بخش از مقاله رسم مدار منطقی تمام NAND و تمام NOR آموزش داده شده و با مشاهده مثال زیر میتوانید با مراحل رسم مدار منطقی آشنا شوید.
مراحل تمام NAND کردن مدار منطقی
- تابع بولی را به صورت SOP ساده کنید.
- مدار را به صورت AND-OR رسم کنید.
- هر گیت AND را به AND- invert و گیت OR را به invert-OR تبدیل می‌کنیم. به عبارت ساده تر در هر مسیر دو حباب یکی در خروجی گیت AND و یکی در هر ورودی گیت OR قرار می دهیم و در نهایت گیت invert-OR را حذف و به جای آن از گیت NAND استفاده می‌کنیم.
به مثال زیر توجه کنید:
F = A⸍BC⸍ + A⸍BC + AB⸍C⸍ + ABC⸍
فرم ساده شده تابع F به صورت SOP برابر است با:
F(SOP) = A⸍B + AC⸍
مدار تابع F در شکل زیر نشان داده شده است.
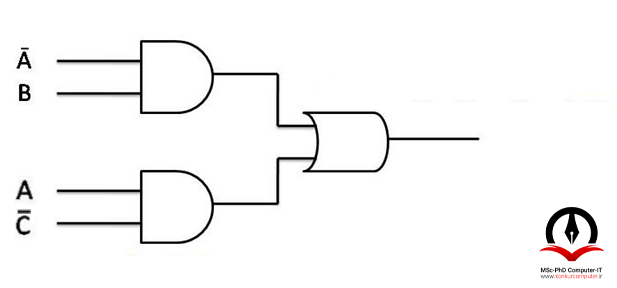
حباب گذاری را بر روی مدار اعمال می کنیم.
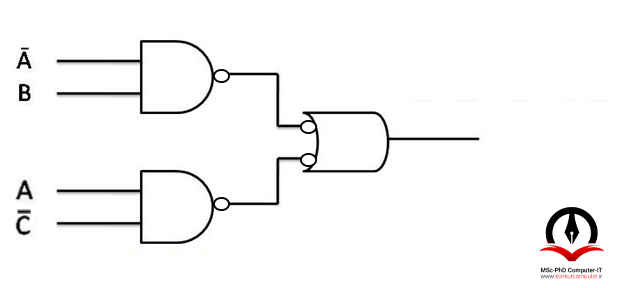
و در نهایت گیت invert-OR را به گیت NAND تبدیل می‌کنیم.
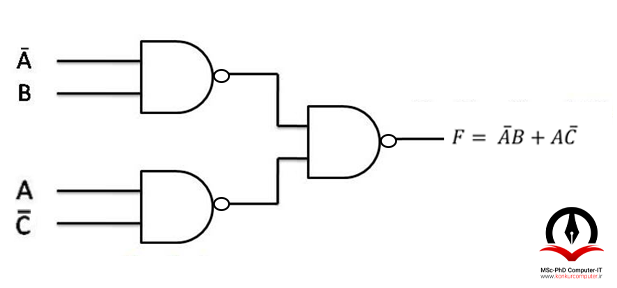
مراحل تمام NOR کردن مدار منطقی
- تابع بولی را به صورت POS ساده کنید.
- مدار را به صورت OR-AND رسم کنید.
- 3. هر گیت OR را به OR- invert و گیت AND را به invert-AND تبدیل می‌کنیم. به عبارت ساده تر در هر مسیر دو حباب یکی در خروجی گیت OR و یکی در هر ورودی گیت AND قرار می دهیم و در نهایت گیت invert-AND را حذف و به جای آن از گیت NOR استفاده می‌کنیم.
به مثال زیر توجه کنید:
F = A⸍B⸍C⸍ + A⸍BC⸍ + A⸍BC + ABC
فرم ساده شده تابع F به صورت POS برابر است با:
F(POS) = (B + C⸍) . (A⸍ + C)
مدار منطقی تابع F در شکل زیر نشان داده شده است.
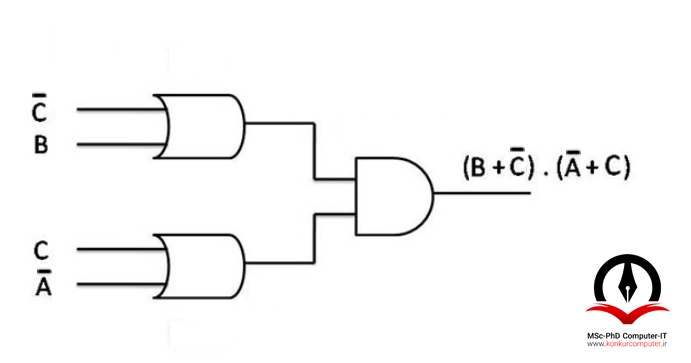
بر روی مدار حباب‌گذاری می‌کنیم.
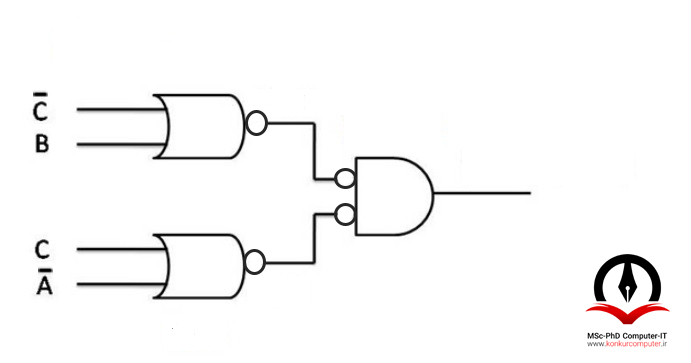
در نهایت گیت invert-AND را به گیت NOR تبدیل می‌کنیم.
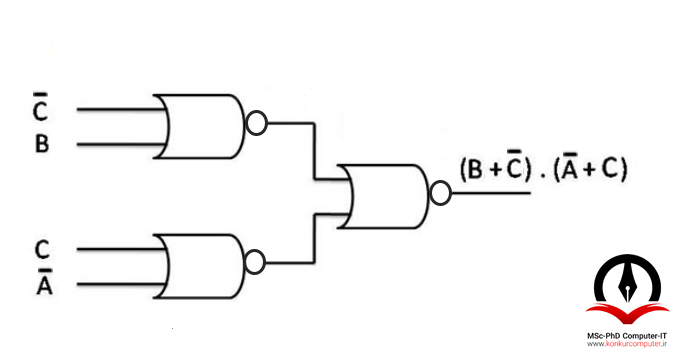
نمایش اعداد در سیستم های دیجیتال
هر چند که انسان برای نمایش اعداد و انجام محاسبات ریاضی عمدتا از مبنای 10 استفاده می‌کند در کامپیوترها و سیستمهای دیجیتال معمولا از مبنا 2 برای نمایش اعداد و انجام محاسبات ریاضی استفاده میشود. دلیل این مسئله به نحوه پیاده سازی و ساخت سیستمهای دیجیتال بر می‌گردد. در مبنا 2 تنها از دو رقم 0 و 1 استفاده میشود. همچنین عناصر مورد استفاده در سیستمهای دیجیتال معمولا 2 حالته هستند، مثلا ترانزیستورهای مورد استفاده در سیستمهای دیجیتال در یکی از دو حالت خاموش یا روشن عمل میکنند، به همین دلیل دو رقمی بودن مبنا 2 موجب شده است که این مبنا تناسب بیشتر با ذات سیستم‌هایِ دیجیتالِ مورد استفاده در دنیای امروز داشته باشد و در طراحی و تحلیل مدارهای منطقی مبنای 2 از اهمیت زیادی برخوردار است. رایج است که برای دو رقم مورد استفاده در مبنای 2 یعنی ارقام 0 و 1 به جای استفاده از اصلاح رقم از اصلاح بیت (Bit) استفاده میشود. حال در مدارهای منطقی اطلاعات به صورت سیگنال‌های الکترونیکی نمایش داده می‌شوند. در مدارهای الکترونیکی دو مقدار 0 و1 به صورت دو سطح ولتاژ پیاده‌سازی می‌شوند: مقدار 0 با ولتاژ صفر (زمین)، و مقدار 1 با ولتاژ منبع تغذیه‌ی مدار.
انواع نحوه نمایش یک تابع
برای بیان و نمایش یک تابع بولی روش‌های متفاوتی وجود دارد که عبارتند از:
- جدول درستی (صحت)
- جمع حاصلضرب ها (SOP)
- ضرب حاصلجمع ها (POS)
- با استفاده از مینترم (Minterm)
- با استفاده از ماکسترم (Maxterm)
1- جدول درستی
جدول درستی یکی از ابزارهای نمایش عملکرد مدارهای منطقی است. هر جدول درستی دارای دو بخش ورودی‌ها (inputs) و خروجی‌ها (Outputs) است. هر مدار منطقی متناسب با تابعی که برای آن تعریف شده، دارای دو یا چند گیت منطقی است که ورودی‌های تابع به این گیت‌ها اعمال شده و با عبور از تمام گیت‌های مدار منجر به تولید یک یا چند خروجی خواهند شد.
باتوجه به اینکه هر ورودی می‌تواند دو مقدار صفر و یک داشته باشد؛ در یک جدول درستی، باید تمام ترکیب‌های ممکن برای وروردی‌ها در نظر گرفته شود. بطور کلی برای مداری با n ورودی، میتوان 2 به توان n حالت در نظر گرفت و خروجی متناظر با هر یک از ورودی‌ها را در مدار محاسبه کرد.
بعنوان مثال در شکل زیر ، یک مدار منطقی با سه ورودی A، B و C که بوسیله دو گیت منطقی NAND و یک گیت NOR به یکدیگر متصل‌اند، نشان داده شده. در جدول درستی متناظر با مدار، 8 حالت (ردیف) برای ورودی‌ها در نظر گرفته شده و در هر ردیف خروجی تابع متناظر (Q) محاسبه شده است.
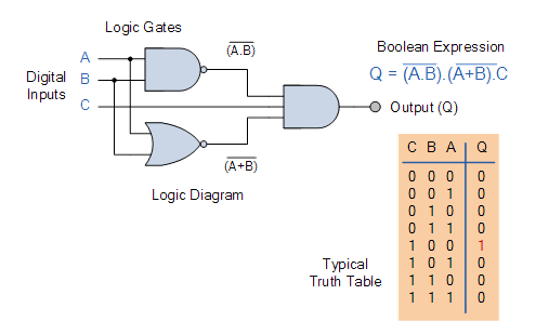
2- بیان یک تابع بصورت جمع حاصلضرب ها (SOP)
زمانی که دو یا چند حاصلضرب با یکدیگر جمع می‌شوند، مفهمومی به نام جمع حاصلضرب ها (sum of products (SOP)) را به وجود می‌آورند. به این معنا که خروجی‌های دو یا چند گیت AND به ورودی های گیت OR وصل می‌شوند و در نهایت خروجی منطقی AND-OR را ایجاد می‌نمایند.
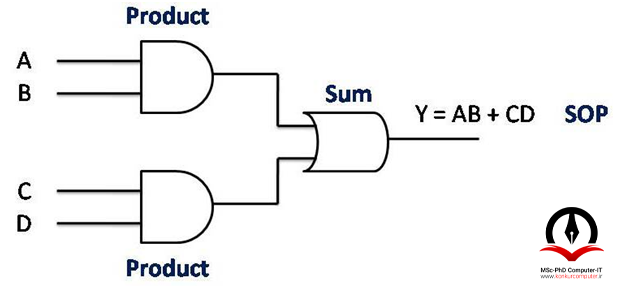
3- بیان یک تابع بصورت ضرب حاصلجمع ها (POS)
این منطق ناشی از حاصلضرب دو یا چند حاصلجمع با یکدیگر است که به آن ضرب حاصلجمع ها (product of sums(POS)) می گویند. زمانیکه خروجی‌های دو یا چند گیت OR به ورودی‌های یک گیت AND متصل شوند در نهایت خروجی با منطق OR-AND بوجود خواهد آمد.
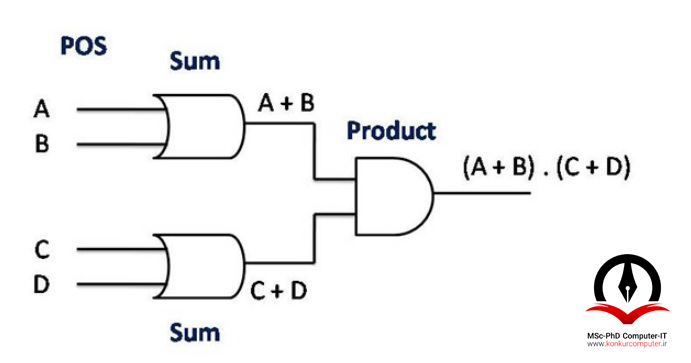
4- بیان یک تابع با استفاده از مینترم‌ها (Minterm)
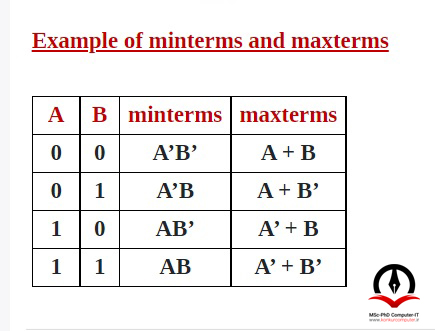
جمله ای است به صورت ضرب میان متغیرها که در آن هر متغیر یا not آن دقیقاْ یکبار ظاهر میشود. مقدار یک مینترم زمانی برابر یک خواهد بود که اندیس مینترم با عدد ورودی یکسان باشد.
5- بیان یک تابع با استفاده از ماکسترم‌ها (Maxterm)
جمله ای به صورت جمع میان متغیرها که در آن هر متغیر یا notاش فقط یکبار ظاهر می شود. یک ماکسترم زمانی که اندیس‌اش با عدد ورودی یکسان باشد مقدارش برابر صفر و در بقیه حالات برابر یک خواهد بود.
ساده سازی توابع بولی
هر تابع را میتوان با عبارت‌های جبری متفاوتی نشان داد و به ازای هر عبارت جبری دقیقا یک مدار منطقی وجود دارد، بنابراین میتوان نتیجه گیری کرد که برای هر تابع مدارهای منطقی زیاد و مختلفی وجود دارد، حال هر چند تمامی مدارهای منطقی که برای یک تابع وجود دارد تابع یکسانی را پیاده سازی میکنند و عملکرد یکسانی دارند ولی هر یک از آنها از نظر تاخیر و پیچیدگی سخت افزار با یکدیگر متفاوت هستند.
حال هر گاه می‌خواهیم برای یک تابع مداری با تاخیر کمتر یعنی تعداد طبقات کمتر و ساده تر (با پیچیدگی سخت افزار کمتر) بیابیم به جای آنکه روی مدار منطقی آن فکر کنیم به عبارت جبری مربوط به تابع فکر می‌کنیم، به بیان دیگر روش‌هایی که از آنها برای دستیابی به سرعت و سادگی در مدارهای منطقی استفاده میشود، روش‌های جبری هستند، یعنی هیچ کدام بر روی مدارهای منطقی اعمال نمی‌شوند بلکه بر روی عبارت‌های جبری اعمال می‌شوند هر چند در نهایت هدف دستیابی به یک مدار منطقی سریع و ساده است.
نکته دیگری که باید به آن اشاره کرد این است که بین سرعت و سادگی در مدارهای منطقی مصالحه وجود دارد و در روش‌های ساده سازی که در درس مدارهای منطقی آموزش داده میشود بر خلاف آنچه که اکثر افراد تصور میکنند اولویت اصلی با سرعت است نه با سادگی مدار، به نحوی که در درس مدارهای منطقی در پی ساده‌ترین مدار نیستیم بلکه در پی ساده‌ترین مدار در میان سریع ترین مدارها هستیم.
برای آشنایی بیشتر با موارد بیان شده و همین طور آشنایی با مزایای ساده سازی توابع در درس مدارهای منطقی فیلم زیر را مشاهده کنید.
ساده سازی مدارهای منطقی و مزایای آن
جدول کارنو در مدار منطقی
همان طور که در بالا اشاره کردیم ما به دنبال ساده ترین مدار در میان سریع ترین مدارها هستیم، با در نظر گرفتن اینکه نقیض هر یک از ورودی های مدار را داریم و با این فرض که برای ساختن مدار فقط از گیت‌های and و or استفاده کنیم در این صورت سریعترین مدارها، مدارهای مبتنی بر SOP یا POS (SOP یعنی جمع حاصلضرب‌ها و POS یعنی ضرب حاصلجمع‌ها) هستند که دارای حداکثر دو طبقه هستند، حال چون ما می‌خواهیم ساده‌ترین مدار را از میان سریعترین مدارها بیابیم به دنبال یافتن ساده‌ترین SOP یا ساده ترین POS هستیم. توجه کنید که ساده ترین SOP یا ساده ترین POS را ممکن است بتوان ساده‌تر کرد ولی چون شکل آن از SOP یا POS خارج میشود طبقات مدار از دو بیشتر میشود که این یعنی مدار حاصل جز سریعترین مدارها نیست.
برای رسیدن به ساده ترین SOP یا POS دو روش مهم وجود دارد، یکی روش جدول کارنو و دیگری روش کواین مک کلاسکی، چون روش جدول کارنو بصورت گسترده توسط دانشجویان استفاده میشود این روش را بصورت کامل در فیلم زیر آموزش داده‌ایم.
آموزش جدول کارنو
طراحی سطحِ قطعهِ مدارهای منطقی (Component-Level Design)
متوجه شدیم که با اتصال گیت‌های منطقی به یکدیگر می‌توانیم مدارهای منطقی مختلف برای پیاده سازی توابع گوناگون ایجاد کنیم. به متصل کردن گیت‌ها به یکدیگر برای ساختن مدارهای منطقی معمولا طراحی سطح گیت (Gate-Level Design) گفته میشود. روش دیگری برای طراحی و ساخت مدارهای منطقی وجود دارد به نام طراحی سطح قطعه (Component-Level Design)، که در این روش برای ساخت مدارهای منطقی به جای آنکه گیت‌های منطقی را به یکدیگر متصل کنیم، قطعات و اجزائی را به یکدیگر متصل می‌کنیم که هر کدام از این قطعات خود از اتصال گیت‌های متعدد به یکدیگر ساخته شده‌اند. قطعاتی که در طراحی سطح قطعه مدارهای منطقی استفاده میشود به دو دسته تقسیم می‌شوند:
1. قطعات ترکیبی: این قطعات از این جهت ترکیبی نامیده می‌شوند که دارای حافظه نیستند، از جمله قطعات ترکیبی میتوان به موارد زیر اشاره کرد
- دیکودر (Decoder)
- انکودر (Encoder)
- انکودر اولویت دار (Priority Encoder)
- مالتی پلکسر یا تسهیم کننده (Multiplexer)
- دی مالتی پلکسر (Demultiplexer)
- مدار جمع کننده (Adder)
- مدار مقایسه کننده (Comparator)
2. قطعات ترتیبی: این قطعات دارای حافظه هستند، یعنی در ساختار درون آنها از فلیپ فلاپ استفاده شده است
قطعات ترکیبی در مدارهای منطقی
دیکودر (Decoder)
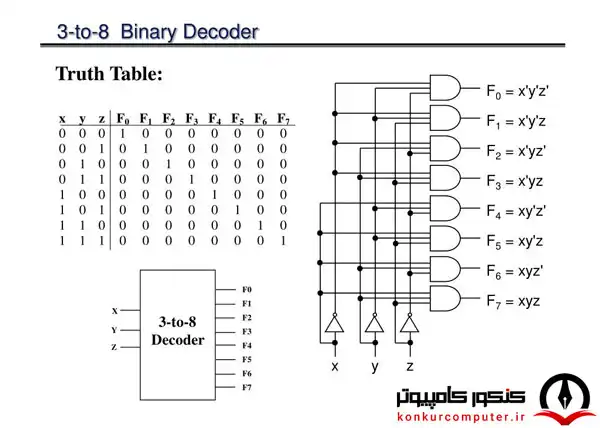
معمولا یک قطعه ترکیبی دیکودر را با علامت اختصاری DEC مشخص میکنند. یک DEC n/2n یک مدار ترکیبی بدون حافظه است که دارای n ورودی و 2n خروجی است، خروجی ها که تعداد آنها 2n تا است را از شماره 0 تا 2n-1 شماره گذاری میکنند. ورودی که تعداد آنها n تا است یک عدد باینری را مشخص می‌کند که چون این عدد n بیتی است مقدار آن از 0 تا 2n-1 است، که این عدد مشخص کننده شماره خروجی است که باید فعال شود. همچنین شما عزیزان میتوانید برای بررسی بیشتر دیکدر به صفحه دیکودرآموزش دیکدر، بررسی انواع دیکودر و کاربرد دیکدر
در این صفحه به آموزش دیکدر، انواع دیکدر، بررسی جدول دیکدر، کاربرد دیکدر و بررسی دیکدر 3 به 8 پرداخته شده است مراجعه کنید.
دیکودر 3 به 8
فیلم معرفی کامل دیکودر
انکودر (Encoder)
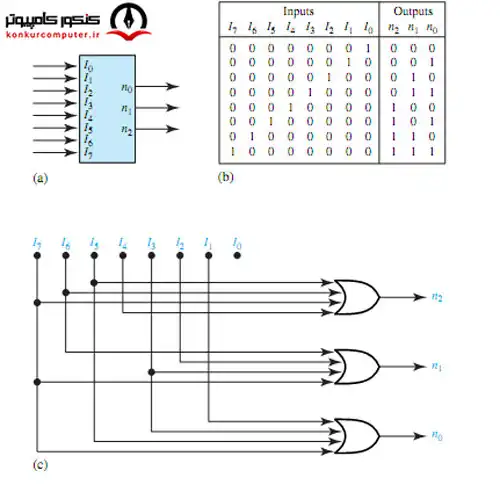
معمولا یک قطعه ترکیبی انکودر را با علامت اختصاری ENC مشخص میکنند. یک ENC 2n/n یک مدار ترکیبی بدون حافظه است که دارای 2n ورودی و n خروجی است، ورودی ها که تعداد آنها 2n تا است را از شماره 0 تا 2n-1 شماره گذاری میکنند. در یک مدار ENC همواره باید یک و فقط یکی از این 2n ورودی فعال باشد، نه کمتر و نه بیشتر. حال اگر تعداد ورودی‌های فعال بیش از یک باشد یا اگر هیچ کدام از ورودی ها فعال نباشند، چنین ورودی‌ای یک ورودی ممنونه برای انکودر محسوب میشود و خروجی مدار در این حالت dont care هواهد بود. خروجی ها که تعداد آنها n تاست یک عدد مبنا دو را مشخص می‌کند که چون این عدد n بیتی است مقدار آن از 0 تا 2n-1 است. عددی که مقدار انکودر به عنوان خروجی می‌دهد برابر شماره ورودی فعال شده است. برای آشنایی بیشتر لطفا به مقاله انکودر در مدار منطقیانکودر در مدار منطقی چیست - آموزش 0 تا 100 انکودر مدار منطقی
در این صفحه به بررسی موارد زیر پرداخته شده است : تعریف انکودر، سخت افزار انکودر، جدول درستی انکودر، انواع انکورد و کاربردهای انکودر پرداخته شده است مراجعه نمایید.
انکودر 8 به 3
فیلم معرفی کامل انکودر
انکودر اولویت دار (Priority Encoder)
یادگرفتیم که انکودر مداری است که ورودی و n خروجی دارد و در هر لحظه تنها یکی از ورودی‌ها می‌تواند مقدار «1» داشته باشد و بقیه ورودی‌ها باید در حالت 0 باشند. در صورتی‌که چند ورودی به صورت همزمان در حالت «1» قرار داشته باشند، آن ورودی که اولویت بالاتری نسبت به بقیه دارد، در مدار اثر می‌گذارد. به چنین مداری، انکودر با اولویت گفته میشود. برای n=2 جدول صحت آن به صورت زیر میشود:
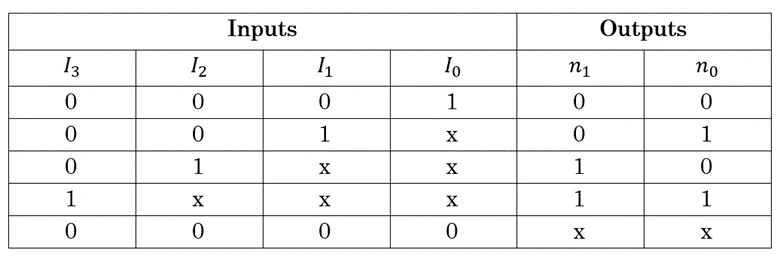
فیلم معرفی انکودر اولویت دار
مالتی پلکسر یا تسهیم کننده (Multiplexer)
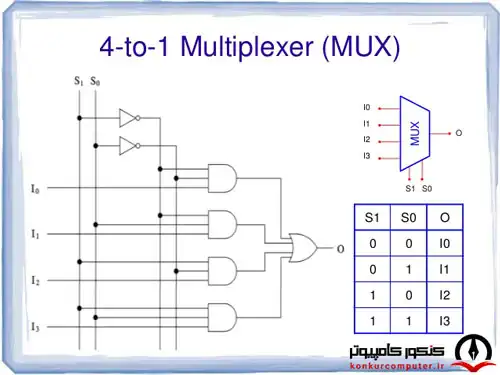
معمولا یک قطعه ترکیبی تسهیم کننده را با علامت اختصاری MUX مشخص میکنند. یک MUX 2n/1 یک مدار ترکیبی بدون حافظه است که دارای دو گروه ورودی است، گروه اول ورودی‌های داده است که تعداد آنها 2n است و آنها را با D0 و D1 و ... و D2n-1 نشان می‌دهیم و گروه دوم ورودی های انتخاب است که تعداد آنها n عدد است و معمولا آنها را با S0 و S1 و ... و Sn-1 نشان می‌دهیم. هر مالتی پلسر فقط یک خروجی دارد. ورود‌های انتخاب که تعداد آنها n تا است یک عدد مبنای دو را مشخص میکنند که چون این عدد n بیتی است مقدار آن از 0 تا 2n-1 است. این عدد مشخص کننده شماره داده ای است که باید روی خروجی برود. در مالتی پلکسر خروجی برابر یکی از ورودی هاست و آن ورودی داده، ورودی ای است که شماره آن توسط خطوط انتخاب مشخص میشود. برای مشخص تر شدن نحوه کار یک تسهیم کننده، شکل یک MUX 4/1، جدول درستی آن و شکل مدار داخلی آن را در زیر برای شما آورده ایم.
مالتی پلکسر 4 به 1
فیلم معرفی کامل مالتی پلکسر
دی مالتی پلکسر (Demultiplexer)
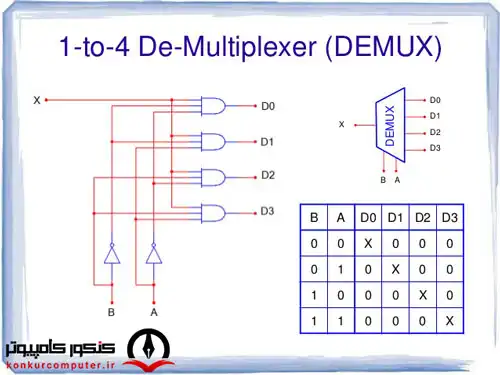
معمولا یک قطعه ترکیبی دیمالتی پلکسر را با علامت اختصاری DEMUX مشخص میکنند. همان طور که از نام DEMUX میتوان حدس زد عملکرد این قطعه دقیقا برعکس عملکرد تسهیم کنند است. یک DEMUX 1/2n دارای 2n خروجی است که با D0 و D1 و ... و D2n-1 مشخص میشود و دارای مجموعا n+1 ورودی است که یکی از این ورودی ها را با I نشان می‌دهیم و این ورودی، وروی داده است و سایر ورودی‌ها، ورودی‌های انتخاب هستند که با S0 و S1 و ... و Sn-1 نشان داده می‌شوند. ورود‌های انتخاب که تعداد آنها n تا است یک عدد مبنای دو را مشخص میکنند که چون این عدد n بیتی است مقدار آن از 0 تا 2n-1است. این عدد مشخص کننده شماره خروجی است که داده ورودی (I) به آن منتقل میشود. برای مشخص تر شدن نحوه کار یک دیمالتی پلکسر، شکل یک DEMUX 1/4، جدول درستی آن و شکل مدار داخلی آن را در زیر برای شما آورده ایم.
دی مالتی پلکسر 1 به 4
فیلم معرفی کامل دی مالتی پلکسر
مدار جمع کننده (Adder)
مدار جمع کننده همانطور که از اسمش مشخص است، جمع اعداد را برای ما انجام می‌دهد. مدارات جمع کننده خود به دو دسته‌ی نیم جمع کننده (Half Adder - HA) و تمام جمع کننده (Full Adder - FA) تقسیم می‌شوند. HA برای ما جمع دو بیت را انجام داده و در حاصل به ما حاصل جمع (Sum) و رقم نقلی خروجی (Carry Out) را می‌دهد. جدول صحت، شکل مدار و همچنین توابع خروجی‌های آن به صورت زیر است:
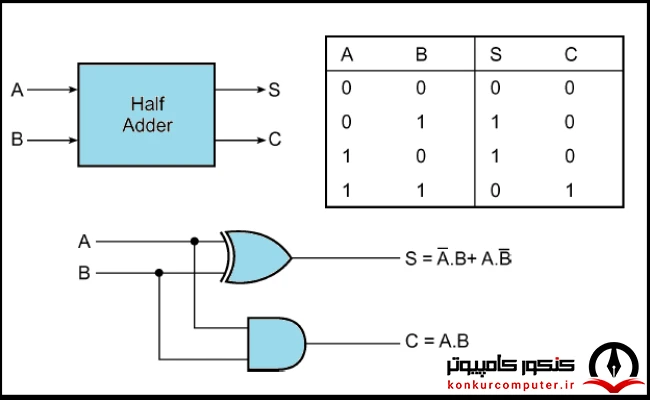
مدار FA حاصل جمع سه بیت را بدست می‌آورد و در غالب دو خروجی به نام‌های حاصل جمع (Sum) و رقم نقلی خروجی (Carry Out) برای ما نمایش می‌دهد. جدول صحت و شکل آن به صورت زیر است:
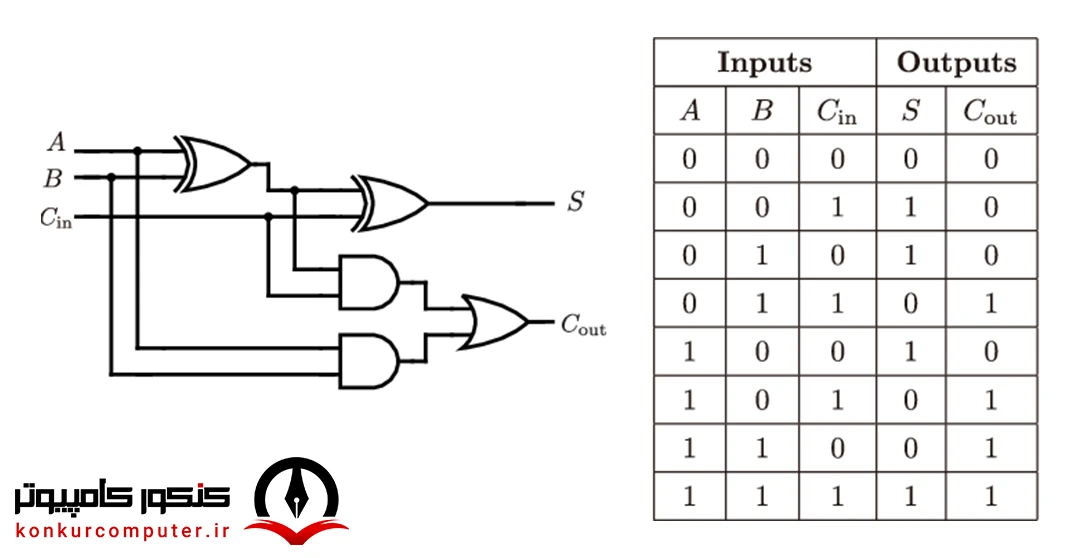
مدار مقایسه کننده (Comparator)
مدار مقایسه کننده مداری است که دو عدد را به عنوان ورودی دریافت کرده و با توجه به وضعیت آن دو عدد نسبت به هم، یکی از پایه‌های خروجیِ E (برابری)، L (کوچکتر) و G (بزرگتر) فعال میشود که در واقع به این معنی است که دو عدد را با یک دیگر مقایسه کرده و به ما می‌گوید که عدد اول، برابر یا بزرگتر یا کوچکتر از عدد دوم است. جدول صحت زیر مقایسه دو عدد 2 بیتی A و B را به همراه مدار آن نشان می‌هد:
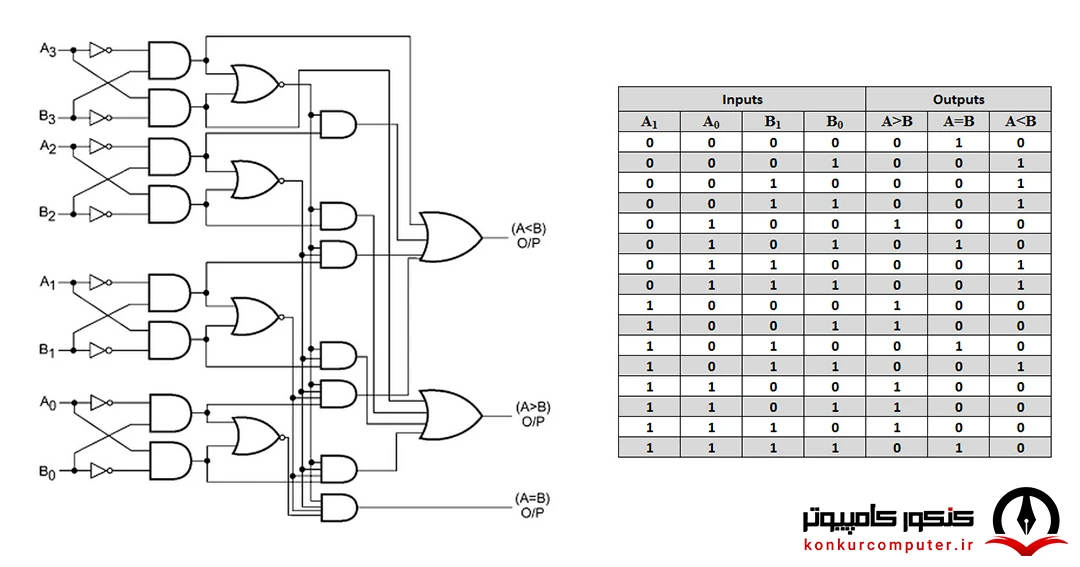
فیلم معرفی مقایسه کننده
قطعات ترتیبی در مدارهای منطقی
لچ یا مدار نگهدارنده (Latch)
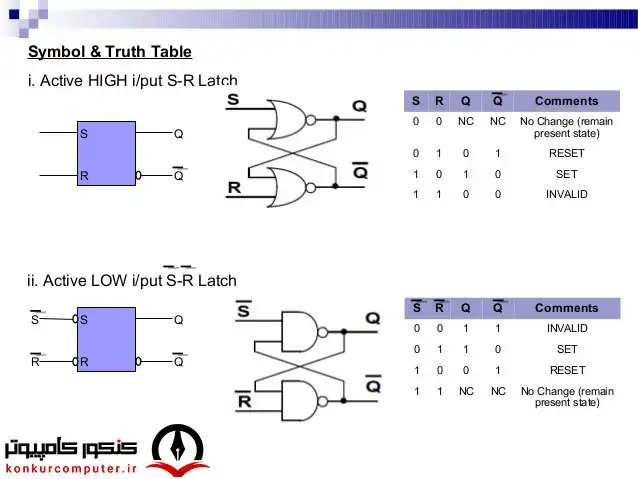
لچ مداری است که توانایی ذخیره یک بیت داده را دارد و دارای دو ورودی با نام های R و S است. در این مدار برای نوشتن 1 کافی است که مقدار پایه های ورودی R و S را برابر RS=01 و برای نوشتن مقدار 0 کافی است که پایه‌های ورودی R و S را برابر RS=10 قرار دهیم. پس از آنکه ما مقدار 0 و 1 را بوسیله پایه‌های کنترل R و S در لچ نوشتیم، با تغییر پایه های کنترلی به RS=00 می‌توانیم این مقادیر را در لچ حفظ کنیم (نگه داریم).
شکل داخلی لچ SR
فلیپ فلاپ (Flip-Flop)
در سیستمهای دیجیتال نیاز است که از تعداد زیادی لچ برای نگهداری داده ها استفاده شود، همچنین در سیستمهای دیجیتال لازم است که لچ های مورد استفاده در مدارهای منطقی هنگامی که می‌خواهند تغییر مقدار دهند بصورت هماهنگ و همزمان با هم این کار را انجام دهند، برای رسیدن به این هماهنگی از سیگنالی به سیگنال ساعت (Clock signal) استفاده میشود، بدین منظور سیگنال ساعت به تمامی لچ های موجود در مدار متصل میشود و تغییرات آنها را با یکدیگر هماهنگ می‌کند. وقتی کلاک را به لچ وصل می‌کنیم به مدار جدید فلیپ فلاپ می‌گویند. ما فیلیپ فلاپ های مختلفی داریم از جمله فلیپ فلاپ D و SR و T و JK. یک فلیپ فلاپ می‌تواند حساس به سطح کلاک باشد یا حساس به لبه کلاک، هر فلیپ فلاپ حساس به سطح کلاک می‌تواند حساس به سطح منفی کلاک باشد یا حساس به سطح مثبت کلاک، همچنین هر فلیپ فلاپ حساس به لبه می‌تواند حساس به لبه منفی کلاک باشد یا حساس به لبه مثبت کلاک.
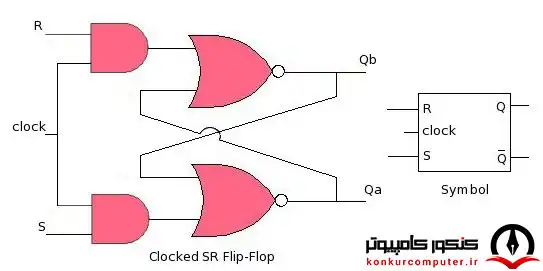
در شکل زیر یک فلیپ فلاپ RS حساس به سطح مثبت را مشاهده می‌کنید، در فلیپ فلاپ RS حساس به سطح مثبت وقتیکه CLK=0 است، لچ مقدارش را حفظ می‌کند و تغییر ورودی های R و S در این زمان ها اثری ندارند، هنگامیکه CLK=1 است ورودی های کنترلی R و S در تعیین مقدار لچ موثر هستند، در این وضعیت اگر RS=10 باشد مقدار لچ برابر 0 میشود، اگر RS=01 باشد مقدار لچ برابر 1 میشود و اگر RS=00 باشد مقدار نگهدارنده حفظ میشود، توجه کنید که ورودی RS=11 یک ورودی ممنونه است که نباید به فلیپ فلاپ RS اعمال شود.
شکل داخلی فلیپ فلاپ SR
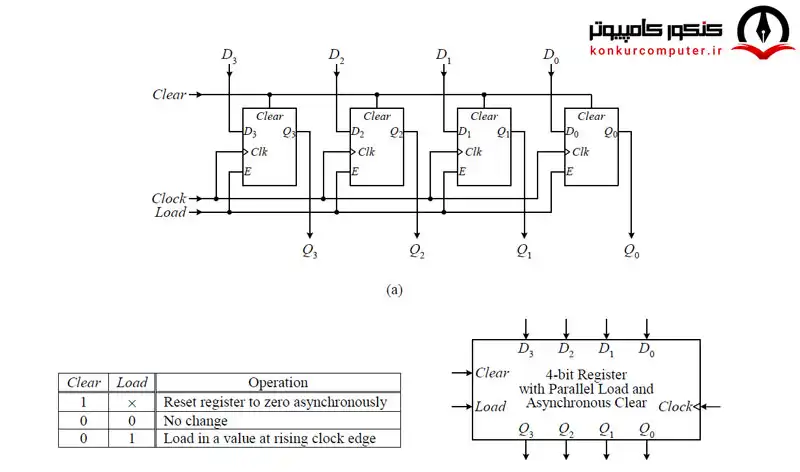
ثبات (Register)
به گروهی از فلیپ فلاپ ها در کنار هم ثبات گفته میشود، به بیانی دیگر یک ثبات متشکل از گروهی از فلیپ فلاپ هاست که معمولا از یک نوع (به خصوص از نوع فلیپ فلاپ
مدار داخلی یک رجیستر 4 بیتی
سوالی که در اینجا ممکن است مطرح شود این است که بر چه اساسی فلیپ فلاپ‌های موجود در یک سیستم دیجیتال به ثبات‌ها دسته بندی می‌شوند؟ مثلا اگر در یک سیستم دیجیتال 16 تا فلیپ فلاپ داشته باشیم آیا تمام این فلیپ فلاپ‌ها را میتوان در قالب یک ثبات 16 بیتی دسته بندی کرد؟ یا آیا میشود آنها را به شکل 4 ثبات 4 بیتی در نظر گرفت؟ در صورتی که بتوانیم فلیپ فلاپ ها را به شکل 4 ثبات 4 بیتی در نظر بگیریم کدام فلیپ فلاپ ها باید کنار هم قرار گرفته و تشکیل ثبات دهند؟ پاسخ این سوالات این است که معمولا طراح یک سیستم دیجیتال آن فلیپ فلاپ‌هایی را در کنار هم به عنوان یک ثبات در نظر می‌گیرد که داده‌های درون آن فلیپ فلاپ‌ها از نظر معنایی که دارند به هم مربوط باشند.
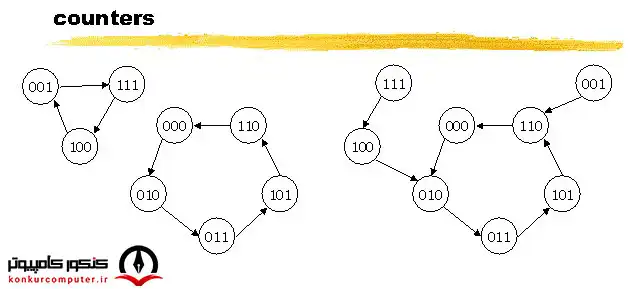
شمارنده (Counter)
می‌دانیم که برای هر مدار ترتیبی می‌توانیم دیاگرام حالت اش را نیز بکشیم، حال به مدار ترتیبی که درون دیاگرام حالت اش چرخه ای وجود داشته باشند شمارنده می‌گویند، یا به بیانی دیگر به مدار ترتیبی که تعدادی حالت را در یک چرخح بطور تکراری سپری کند شمارنده گفته میشود، توجه به این نکته ضروری است که الزامی ندارد که کدهای تخصیص داده شده به حالت های یک شمارنده اعداد متوالی باشند. بعنوان مثال دیاگرام حالت یک شمارنده می‌تواند بصورت زیر باشد:
نمونه هایی از دیاگرام حالت های شمارنده
انواع مدار منطقی
دو نوع اصلی مدار منطقی وجود دارد:
مدارات ترکیبی
مدارات ترکیبی از گیت‌های منطقی مختلفی ساخته می‌شوند. پیاده سازی این مدارات به گونه‌ای است که خروجی تنها به مقادیر حال حاضر ورودی‌ها بستگی دارد، یعنی خروجی مدار متاثر از عملکرد مدار در گذشته نیست.
انواع مدارات ترکیبی عبارتند از:
- مدارهایی جهت انجام عملیات منطقی و حسابی مانند: جمع کننده، تفریق کننده، مقایسه کننده‌ها، مدارات منطقی برنامه پذیر و ...
- مبدل‌های کد (Code Converters) مانند: BCD و کد افزونه 3 (Excess-3 BCD) و ...
- دیگر عناصر انتقال دهنده داده مانند: Encoder, Decoder, Multiplexer, Demultiplexer و ...
مدارات ترتیبی
مدارات ترتیبی از مدارات ترکیبی و المان‌های حافظه تشکیل شده‌اند. این مدارها به گونه‌ای پیاده سازی شده‌اند که خروجی مدار فقط به ورودی های آن بستگی ندارد بلکه به تاریخچه گذشته ورودی های آن نیز بستگی دارد، به عبارت دیگر مدار ترتیبی دارای حافظه است.
به منظور درک بهتر عملکرد این نوع مدارات مثال کنترل تلویزیون را بیان می‌کنیم. هنگامی که شما در شبکه‌ی 2 قرار دارید و دکمه Up کنترل را جهت عوض کردن شبکه میفشارید، میبینید که شبکه تلویزیون به شماره 3 تغییر پیدا کرد. این یعنی مدار داخلی تلویزیون حالت فعلی شما را (شبکه 2) ذخیره داشته و به محض فشردن دکمه Up، با توجه به ورودی کنترل و حالت فعلی شبکه، خروجی (شبکه 3) را برای شما نمایش می‌دهد.
انواع مدارات ترتیبی عبارتند از:
- مدارات ترتیبی سنکرون: مدارهای ترتیبی آسنکرون مداراتی هستند که از پالس کلاک استفاده نمی‌کنند. به عبارتی حالت‌های داخلی با تغییر متغیرهای ورودی، بدون در نظر گرفتن کلاک، تغییر میکنند.
- مدارات ترتیبی آسنکرون: در مدارهای ترتیبی سنکرون، همگام سازی حالت عنصر حافظه توسط سیگنال کلاک انجام می شود. به عبارتی تغییرات ورودی همزمان با اعمال پالس کلاک به مدار تاثیر خود را می‌گذارند. همگام سازی خروجی‌ها یا با لبه‌های منفی سیگنال ساعت یا با لبه‌های مثبت انجام میشود.
به عنوان مثال‌هایی از مدارهای ترتیبی میتوان به لچ (Latch)، فلیپ فلاپ (Flip-Flop)، شمارنده (Counter)، ثبات (Register) و ... اشاره کرد.
ساخت و تولید مدارهای منطقی
از مدارهای منطقیآموزش مدار منطقی به زبان ساده - بررسی مدار منطقی و انواع آن
امروزه درک صحیحی از مدارهای منطقی برای هر مهندس برق و کامپیوتر ضروری است. این مدارها عنصر اصلی کامپیوترها و بسیاری از وسایل الکترونیکی اطراف ما هستند، در این صفحه به بررسی و آموزش مدار منطقی پرداخته شده است برای ساخت سخت‌افزار کامپیوتر و بسیاری محصولات دیگر استفاده میشود، که همگی آنها را تحت نام سخت‌افزار دیجیتال (Digital Hardware) طبقه‌بندی می‌کنیم. نام دیجیتال از روش نمایش اطلاعات در کامپیوترها گرفته شده است، که در آنها سیگنال‌های الکترونیکی به عنوان عدد تعبیر میشود.
مدارهای منطقی روی تراشه‌های نیمه‌رسانا و با استفاده از ترانزیستور و سایر عناصر الکترونیکی پیاده‌سازی میشود. اغلب تراشه‌های امروزی (از جمله پردازنده‌های کامپیوتری) بیش از یک میلیارد ترانزیستور دارند. شناخت اجرای سازنده‌ی این مدارها به سادگی امکان‌پذیر است، ولی مداری با بیش از یک میلیارد ترانزیستور را اصلاً نمی‌توان چیز ساده‌ای دانست پیچیدگی ذاتی چنین مدارهایی را فقط به کمک روش‌های طراحی بسیار سازمان‌یافته میتوان تحت کنترل درآورد. در زیر کمی درباره‌ی فناوری‌های سخت‌افزاری مورد استفاده در تولید و ساخت مدارهای منطقی صحبت خواهیم کرد.
فناوری ساخت و تولید سخت افزارسخت افزار چیست - بررسی اجزای اصلی سخت افزار کامپیوتر
در این صفحه بررسی شده که سخت افزار چیست و سخت افزار کامپیوتر به زبان ساده معرفی شده است، همچنین به بررسی اجزای اصلی سخت افزار کامپیوتر پرداخته شده استهای دیجیتال در طول چند دهه‌ی گذشته به شدت دچار تحول شده است تا اواسط دهه‌ی 1960 مدارهای منطقی با مونتاژ کردن قطعات حجیم و منفصل، مانند ترانزیستورها و مقاومت‌های مجزا، ساخته می شدند. با اختراع مدارهای مجتمع یا آی سیآی سی (IC) چیست؟ بررسی وظایف و اهمیت چیپ ها در کامپیوتر
آیسیها نقش پررنگی در زندگی امروز بشر ایفا میکنند، آنها در وسایلی همچون موبایل، کامپیوتر، یخچال، ماشین‌ها، هواپیما و ... حضور دارند، بنابراین آشنایی با آی‌سی برای علاقه‌مندان به رشته کامپیوتر از اهمیت بالایی برخوردار است، به همین علت در این مقاله به معرفی و بررسی IC پرداخته شده است. (Integrated Circuit- IC) امکان قرار دادن تعداد زیادی ترانزیستور (و بنابراین یک مدار کامل) روی یک تراشه‌ی نیمه هادی فراهم شد.
یک واحد پردازنده مرکزی(CPU) نیز یک نوع آی سی یا چیپ محسوب میشود که ازمیلیون‌ها ترانزیستور میکروسکوپی تشکیل شده و قابلیت اجرای محاسبات و برنامه‌های کامپیوتری ذخیره شده در حافظه را امکان پذیر می‌سازد. برای آشنایی بیشتر با پردازنده (CPU)پردازنده (CPU) چیست؟ بررسی انواع، وظایف و کاربردها
سی پی یو قلب کامپیوتر و کامپیوتر قلب دنیای کنونی است، بنابراین در این صفحه به معرفی و بررسی سی‌پی‌یو یا همان پردازنده مرکزی (CPU) پرداخته شده، و بطور کامل توضیح داده‌ایم که CPU از چه بخش هایی تشکیل شده و هر بخش چه وظایف و مشخصاتی دارد. پیشنهاد میدهم که به مقاله آن در صفحه کنکور کامپیوتر مراجعه فرمائید.
تاریخچه‌ای تصویری از تکامل مدارهای مجتمع یا آی سی در طول زمان
ساخت یک کامپیوتر
برای درک نقش مدارمنطقی کامیپوتر یا سیستمهای دیجیتال، اجازه دهید ساختمان یک کامپیوتر را در نظر بگیریم؛ در داخل بدنه کامپیوتر تعدادی بورد مدار چاپی (PCB)، یک منبع تغذیه، و واحدهای ذخیره‌سازی مانند هارد دیسک و درایوهای CD و DVD، قرار دارند. همه‌ی این واحدها به PCB اصلی کامپیوتر که به motherboard معروف است، متصل می‌شوند. همانطور که در قسمت پایین شکل الف میبینید، خود بورد مادر از تعداد زیادی تراشه‌ی مدار مجتمع ساخته شده است که بوردهای دیگر (مانند بوردهای صدا، تصویر و شبکه) از طریق شکاف‌های توسعه به آن وصل می‌شوند.
ساختار یکی از این تراشه‌های مدار مجتمع در شکل ب نشان داده شده است. در این تراشه تعدادی زیرمدار (Sub Circuit) وجود دارد که اتصال آنها به یکدیگر مدار کامل را می‌سازد. برای مثال، یک تراشه‌ی ریزپردازنده دارای زیر مدارهایی برای اجرای عملیات ریاضی، ذخیره‌سازی داده، و یا کنترل جریان داده بین بخش‌های مختلف تراشه است. هر کدام از این زیرمدارها یک مدار منطقی است. همانطور که در وسط شکل ب نشان داده شده، یک مدار منطقی خود از به هم پیوستن چند گیت منطقی (Logic Gate) تشکیل میشود.
درس مدار منطقی اساساً درباره‌ی بخش مرکزی شکل ب است، یعنی طراحی مدارهای منطقی. در درس مدار منطقی به چگونگی طراحی مدارهای منطقی برای انجام عملکردهای مهم- مانند جمع، تفریق یا ضرب اعداد، شمارش، ذخیره کردن داده، و کنترل پردازش اطلاعات پرداخته میشود و نشان داده میشود که چگونه میتوان رفتار این مدارها را تعریف کرد، چگونه میتوان آنها را با کمترین هزینه و بیشترین سرعت عملیاتی طراحی کرد، و چگونه میتوان برای اطمینان از عملکرد صحیح این مدارها آنها را آزمایش کرد. در ادامه برخی از سرفصل ها و مباحث درس مدار منطقی به اختصار توضیح داده شده است.
شکل الف : یک سیستم سخت افزار دیجیتال
.webp)
شکل ب : نگاهی به درون یک چیپ
.webp)
کاربرد مدار منطقی
در فناوری‌های مدرن، مدارهای منطقی در دستگاه‌ها و قطعات مختلفی از جمله واحدهای منطقی حسابی (ALU)، حافظه رایانه (Memory) و ثبات‌ها (Register)، مالتی پلکسرها و رمزگشا/رمزگذار یافت می‌شوند. این مدارات در ریزپردازنده‌های ارتقا یافته نیز استفاده می‌شوند که برخی از آنها می‌توانند بیش از 100 میلیون گیت داشته باشند.
همچنین گیت‌های منطقی بلوک‌های سازنده الکترونیک دیجیتال هستند و از ترکیب ترانزیستورها به منظور تحقق بخشی عملیات دیجیتالی ساخته می‌شوند. هر محصول دیجیتال از جمله رایانه‌های شخصی، تلفن‌های همراه، تبلت‌ها، ماشین حساب‌ها و ساعت‌های دیجیتال از گیت‌های منطقی استفاده میکنند. از دیگر کاربردهای مدار منطقی میتوان به موارد زیر اشاره کرد:
- رادیوها و دستگاه‌های ارتباطی
- کارت‌های هوشمند (Smart Card)
- مبدل‌های دیجیتال به آنالوگ (DAC)
- مبدل‌های آنالوگ به دیجیتال (ADC)
- ساخت Signal Generator و ...
به طور کلی، بیشتر کارهای انجام شده در یک دستگاه الکترونیکی توسط مدارهای منطقی انجام می‌گیرد . مثلاْ همین الان که شما در حال مطالعه این مقاله در موبایل، رایانه و یا تبلت خود هستید، مدارهای منطقی به طور مداوم در تلاشند تا کلمات این مقاله را در مقابل چشمانتان نمایش دهند.
اما هریک از مدارت منطقی متناسب با ساختارشان کاربردهای متفاوتی دارند. در پایین کاربرد هریک از گیت‌ها به صورت جداگانه آورده شده است.
کاربرد گیت AND :
در بیشتر موارد از گیت AND بعنوان پایه‌های فعال کننده/بازدارنده و به عنوان دروازه‌هایی برای عبور و یا ممانعت از انتقال داده‌ها در مدارهای دیجیتال استفاده میشود. در یک گیت AND بعنوان پایه فعال‌کننده (Enable) ، یکی از ورودی‌های گیت همیشه ثابت و برابر با عدد یک است و ورودی دیگر هرچه که باشد چه صفر و چه یک در خروجی گیت AND ظاهر و اجازه ورود به مدار را پیدا می‌کند.
در مقابل اگر گیت AND بعنوان پایه بازدارنده (inhibitor) باشد، یکی از پایه‌های گیت به صورت ثابت صفر و فارغ از آنکه چه ورودی‌های دیگری به آن وارد میشود مانع از ورود هرگونه سیگنالی به مدار خواهد شد.
کاربرد گیت OR:
یکی از رایج‌ترین کاربردهای گیت OR ، استفاده از آن در ساخت مدارهای هشداردهنده خطر است. یک مدار هشداردهنده به سنسورهایی متصل است که وظیفه شناسایی هرگونه خطا و یا خطر در محیط را دارند. هرگاه هریک از این سنسورها در صورت بروز خطا در سیستم سیگنالی ایجاد کند، یکی از ورودی‌های گیت OR یک میشود و در نتیجه خروجی گیت یک خواهد بود و آلارم سیستم را فعال می‌کند.
بعنوان مثال نمودار پایین تصویری از گیت OR بکاررفته در مدار تشخیص دما و فشار است که هرگاه هریک از فاکتورهای دما یا فشار از حد مجاز خود عبور کنند، سنسور سیگنالی تولید کرده و به مقایسه کننده داده و سپس به گیت OR می‌فرستند، تا گیت OR آن را به میکروکنترلر ارسال و در نهایت دستگاه را خاموش کند.
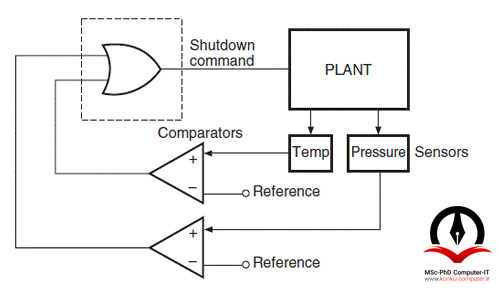
کاربرد گیت NAND:
احتمالاْ به این مورد توجه کردید که وقتی درب فریزر یا یخچال برای مدت طولانی باز می‌ماند، آلارمی شروع به نواختن می‌کند و این دقیقا به دلیل وجود گیت NAND در ساختار مدار زنگ هشدار است. مثالی دیگری از کاربرد گیت NAND، بکارگیری این گیت‌ها در مدارهای کنترل خودکار دمای درون کولرهای گازی و ثابت نگه داشتن دمای محیط است.
این مدارها از طریق سنسورهای اندازه گیری دما، به محض آنکه دما از میزان حدمجاز بالاتر رفت سیگنالی را به میکروکنترلر ارسال کرده و در نهایت موجب روشن شدن کندانسور و خنک کردن محیط تا دمای تعیین شده می‌شوند.
کاربرد گیت NOT :
به گیت NOT ، معکوس کننده نیز گفته می شود، چرا که سیگنال ورودی را معکوس و سیگنال مخالف را در خروجی تولید می‌کند. گیت های NOT در اینورترهای CMOS برای تولید شکل موج و مدارهای آشکارساز دما بسیار پرکاربردند.
دانش مدار منطقی در چه مشاغلی از کامپیوتر کاربرد دارد؟
چون دانش مدار منطقی بعنوان پیش‌نیازی برای ساختمان و معماری کامپیوتر بکار می‌رود به همین دلیل تمام افرادی که در حوزه کاری خود با ساختار کامپیوتر و مدارهای دیجیتالی سرو کار دارند باید از دانش خوبی در زمینه مدارهای منطقی برخوردار باشند. اولین شغلی که بطور مستقیم با ساز و کار مدارهای منطقی ارتباط تنگاتنگی دارد، مهندسی سخت افزار کامپیوتر است. یک مهندس سخت افزار برای طراحی و توسعه راه‌حل‌های معماری و به روز کردن تجهیزات موجود کامپیوتر و آماده کردن آنها برای کار با نرم‌افزارهای جدید، همواره نیازمند دانشی در خصوص مدارهای دیجیتال و سیستمهای تعبیه شده است. شغل‌هایی نظیر توسعه دهنده بلاک چین، توسعه دهندگان نرم افزار و اپلیکیشن‌های موبایل،مدیر امنیت سیستم ها و مدیر امنیت شبکه از جمله مشاغلی هستند که به واسطه آشنایی آنها با معماری کامپیوتر آموزش جامع معماری کامپیوتر
در مهندسی کامپیوتر، معماری کامپیوتر مجموعه‌ای از قوانین و روش‌هایی است که به چگونگی طراحی، کارکرد، سازماندهی و پیاده سازی (ساخت) سیستمهای کامپیوتری می‌پردازد، در این صفحه به بررسی و آموزش کامل معماری کامپیوتر پرداخته شده است و شبکه‌ها بطور غیرمستقیم با دانش مدار منطقی در ارتباطند.
درس مدار منطقی رشته برق
درس مدار منطقی یکی از دروس مهم و بین رشته‌ای میان رشته مهندسی برق و همین طور مهندسی کامپیوتر به شمار می‌رود. هدف این درس آشنایی با اصول و تحلیل و طراحی مدارهای منطقی دیجیتال ، طراحی سیستمی توسط مدارهای مجتمع قابل برنامه ریزی (PLD) و زبان توصیف سخت افزار است.
همچنین این درس به عنوان یکی از دروس مشترک آزمون کارشناسی ارشد رشته مهندسی کامپیوتر و مهندسی برق به حساب می‌آید، تنها با این تفاوت که در رشته مهندسی برق تقریباً هر سال یک سوال از مباحث برنامه‌نویسی سخت افزار نیز مطرح گردیده است.
کتابهای مرجع مدار منطقی رشته برق با رشته کامپیوتر کاملاْ یکسان است و داوطلبان کنکور ارشد برق می‌توانند از فیلم های درس و حل تست مدار منطقی استاد رضوی استفاده کنند. بسیاری از داوطلبان کنکور ارشد برق هر ساله با استفاده از این فیلم‌ها به 100 درصد سوالات درس مدار منطقی رشته برق پاسخ داده‌اند.
بررسی درس مدار منطقی در کنکور ارشد کامپیوتر و آی تی
مدار منطقی نمره بیارترین درس در آزمون کارشناسی ارشد مهندسی کامپیوتر و دکتری معماری کامپیوتر است. به جرات می توان گفت که با مطالعه صحیح درس مدار منطقی میتوان به صد در صد سوالات این درس پاسخ داد. درس مدار منطقی ویژگی هایی دارد که همین ویژگی هاست که باعث شده است که درس مدار منطقی را بهترین و نمره بیار ترین درس کنکور ارشد کامپیوتر بدانیم، این ویژگی ها به قرار زیر است:
1) حجم درس مدار منطقی زیاد نیست و میتوان این درس را در زمان بسیار کمتری نسبت به سایر دروس مطالعه کرد، بعنوان مثال اگر شما فیلم های درس مدار منطقی را تهیه کنید اگر 5 روز کامل فیلم ها را نگاه کنید میتوانید این درس را تمام کنید
2) به جرات میتوان گفت که امن ترین درس کنکور ارشد کامپیوتر مدار منطقی است و سالی وجود نداشته که بسیاری از رتبه های زیر 300 کنکور ارشد کامپیوتر این درس را 100 نزنند. برای بررسی این موضوع میتوانید کارنامه های کنکور ارشد کامپیوتر سال های قبل را مشاهده کنید و یا مصاحبه رتبه های برتر کنکور ارشد کامپیوتر را تماشا کنید
3) برای پاسخ به سوالات درس مدار منطقی در سر جلسه کنکور زمانی کمی نیاز است و در حدود 10 تا 15 دقیقه میتوانید به تمامی سوالات این درس پاسخ دهید و بنابراین میتوانید زمانی که باید به درس مدار منطقی اختصاص میدادید را به دروس دیگر اختصاص دهید.
با توجه به موارد گفته شده مشخص است که درس مدار منطقی بهترین درس کنکور ارشد کامپیوتر برای خواندن است، همچنین مدار منطقی دارای ضریب بالایی در اکثر گرایش های کنکور ارشد مهندسی کامپیوتر است، ضریب درس مدار منطقی در گرایش معماری کامپیوتر دارای ضریب ۴ و در گرایش های شبکه های کامپیوتری، رایانش امن، نرم افزار، بیوانفورماتیک، علوم داده، الگوریتم و محاسبات و علوم و فناوری شبکه دارای ضریب 3 و در گرایش های هوش مصنوعی و قرآن کاوی رایانشی دارای ضریب 2 است. با توجه به موارد گفته شده باید این درس را در صدر درسهایی که می‌خواهید بخوانید قرار دهید. اکثر قریب به اتفاق رتبه‌های زیر 200 کنکور این درس را 100 می‌زنند، بنابراین برای کسب رتبه برتر و رقابت با این دسته و ماندن در کورس رقابت میتوانید و باید این درس را صد زد. در کنکور دکتری معماری کامپیوتر نیز 10 تست ضریب 4 از این درس مطرح میشود که این تعداد تست با بالاترین ضریب در کنکور دکتری خود گویای اهمیت فوق العاده این درس در کنکور دکتری معماری کامپیوتر است. برای بررسی دروس دکتری سایر رشته ها و ضرایب آنها میتوانید به صفحه دروس دکتری کامپیوتر مراجعه کنید
درس مدار منطقی جز دروس امن کنکور ارشد کامپیوتر است، امن بوندن به این معناست که اگر این دروس را بصورت مطلوب مطالعه کنید حتما میتوانید در این دروس درصد خوبی را کسب کنید. با توجه به اینکه سوالات این درس امن هستند و همچنین ضریب بالایی در اکثر گرایش ها دارند بنابراین توصیه ما به داوطلبان کنکور ارشد کامپیوتر تمامی گرایش ها این است که حتما این درس را مطالعه کنند و به هیچ عنوان این درس بسیار مهم را برای کنکور ارشد کنار نگذارید. کنار گذاشتن و یا مطالعه کم مدار منطقی به هیچ عنوان عاقلانه نیست و این کار را به هیچ دانشجویی توصیه نمی‌کنیم.
فیلم های درس مدار منطقی
فیلم های مدار منطقی بسیار کامل هستند و مطالب از 0 تا 100 بیان شده اند و حتی افرادی که رشته شان کامپیوتر نیست براحتی می‌توانند این درس را با استقاده از این فیلم ها مطالعه کنند.
متاسفانه به علت پایه ضعیفی که اکثر دانشجویان کامپیوتر کشور دارند هنگامیکه با کتابهای کنکور شروع به مطالعه این درس میکنند چون کتابهای کنکور همه چیز را از پایه درس نداده‌‌اند شروع به مطالعه برای‌شان سخت است، به همین علت در راستای کمک به دانشجویان فیلم‌های جلسات ابتدایی درس مهم مدار منطقی را تحت اختیار دانشجویان کشور قرار داده ایم تا دانشجویان کشور بتوانند شروعی مناسب و حرفه‌ای داشته باشند، سعی کنید قبل از شروع درس مدار منطقی ابتدا جلسات رایگان زیر را تماشا کنید و بعد یا از روی کتاب‌ها مطالعه‌تان را شروع کنید و یا فیلم‌ها را بطور کامل تهیه کنید و از روی فیلم‌ها ادامه دهید. این فیلم‌ها را میتوانید براحتی در زیر مشاهده کنید
فیلم هایی که برای شروع آسان درس مدار منطقی نیاز دارید
فیلم های رایگان مدار منطقی
مدار منطقی جلسه 1
مدار منطقی جلسه 2
مدار منطقی جلسه 3
مدار منطقی جلسه 4
مدار منطقی جلسه 5
مدار منطقی جلسه 6
حل تست مدار منطقی جلسه 1
حل تست مدار منطقی جلسه 2
حل تست مدار منطقی جلسه 3
پاسخ تشریحی مدار منطقی کنکور ارشد کامپیوتر 1403
پاسخ تشریحی مدار منطقی کنکور ارشد کامپیوتر 1402
حل سوالات مدار منطقی کنکور ارشد کامپیوتر 99
حل سوالات مدار منطقی کنکور ارشد کامپیوتر 98
حل سوالات مدار منطقی کنکور ارشد کامپیوتر 97
برای تماشای تمامی فیلم‌های دیگر مدار منطقی میتوانید به لینک رو به رو مراجعه کنید: آموزش مدار منطقی
نظر برخی از رتبه های برتر کنکور ارشد کامپیوتر و آی تی در مورد کیفیت فیلم‌ها
نظر رتبه 1 کنکور ارشد کامپیوتر 1403
نظر رتبه 1 کنکور ارشد کامپیوتر 1403
نظر رتبه 1 کنکور ارشد کامپیوتر 1403
نظر رتبه 1 کنکور ارشد کامپیوتر
نظر رتبه 2 کنکور ارشد کامپیوتر
نظر رتبه 2 کنکور ارشد
نظر رتبه 6 کنکور ارشد کامپیوتر
نظر رتبه 6 کنکور 1400
نظر رتبه 68 کنکور ارشد کامپیوتر 1403
فیلم ها خیلی قابل فهم و روان است
رتبه 9 :فیلم ها بی نقص بود
از پایه ضعیف تا شریف
نطر رتبه 10: کیفیت تدریس استاد رضوی خیلی خوبه
نظر رتبه 16: کیفیت تدریس خیلی عالی بود
جزوه کامل و ویدیوهای خیلی خوب
نحوه انتقال دانش استاد رضوی بینظیر است
ویدیوها خیلی جامع و کامل بودند
واقعا تدریس اساتید عالی بودند
نظر رتبه 8 کنکور 1400
نظر رتبه 2: معماری کامپیوتر و منطقی 100 زدم
نظر رتبه 13 کنکور ارشد کامپیوتر 1401
نظر رتبه 19: تدریس و فن بیان عالی است
نظر رتبه 12 کنکور ارشد کامپیوتر 1401
نظر رتبه 24: خیلی کامل و جامع است
فیلم‌ها بی نظیر بود
نظر رتبه 45: کیفیت فیلم ها خوب بودن
همه دروس عالی تدریس شده بودند
نیار نیست کتاب تهیه کنید
فیلم ها با بیان شیوا و بدون ابهام بود
کیفیت بالا و هزینه مناسب
نظر رتبه 11 کنکور 1400
فیلم‌ها بی‌نیازم کرد
تدریس زیبا و بیان شیوا
فیلم درس و تست کافیست
فیلم های استاد رضوی از همه نظر عالی بودند
کیفیت و نحوه تدریس و قدرت بیان اساتید از همه نظر خوب بود
خیلی راضی بودم درسها خیلی عمیق تدریس میشد
از همه دروس خیلی راضی بودم
نظر پارسا شریعت
ویدیوها از نظر کیفیت عالی بودند
نظر رتبه 43 کنکور
از دروس استاد رضوی خیلی راضی بودم
نظر پیمان هاشمی
نظر رتبه 40 کنکور
تدریس از 0 تا 100
فیلم شما را جلو می‌اندازد
نظر رتبه 50 کنکور 1400
نظر رتبه 67 کنکور 1400
نظر ریحانه حسین زاده
نظر مرتضی اکبری
نظر رتبه 113 کنکور 1400
تاثیر منابع خوب
نظر سامان حسینی
تفاوت منابع مناسب
نظر رتبه 32 کنکور 1400
کیفیت بالا تدریس
نظر شیوا رضازاد
از روی مراجع نخوانید
فیلم ها خیلی مفهومی بودند
همه درس ها فوق العاده بود
از صفر تا صد و کامل هستند
آشنایی با استاد رضوی و کافه تدریس معجزه بود
فیلم ها جامع بودند
کل منابع من از کافه تدریس یا کنکور کامپیوتر بود
دروس واقعا فوق العاده بودند
درسها کامل و روان است
فیلم ها خیلی دقیق و جامع و کامل بودند
ویدیوها بسیار قابل فهم بودند
مطالبی که پوشش داده شده بود واقعا کامل بود
تدریس بسیار شیوا و روان و بدون ابهام
با پایه ضعیف هم فیلم ها را متوجه می شوید
فیلم ها خیلی به من کمک کرد
همه دروس را از کافه تدریس گرفتم
ویدیوهاشون خیلی به من کمک کرد
معرفی دوره درس و حل تست مدار منطقی
از نگاه دانشجویان، قدرت بیان فوق العاده استاد رضوی و پوشش ۱۰۰ درصدی تمامی سرفصل‌ها، نکات و تست‌ها، ویدیوهای درس مدار منطقی را به بهترین ویدیو آموزشی کشور در درس مدار منطقی تبدیل کرده است. در حال حاضر فیلم آموزش مدار منطقی استاد رضوی پرطرفدارترین و پرفروش‌ترین فیلم اموزشی مدار منطقی کشور است و هر سال بیش از ۶۰۰۰ نفر این فیلم را تهیه میکنند، آموزش مدار منطقی به زبان ساده و صفر تا صد دلیل محبوبیت آموزش منطقی است.
در فیلم‌های مدار منطقی تهیه شده بر خلاف فیلم‌های مشابه این فرض در نظر گرفته نشده که دانشجویان باید یکسری از مطالب را از قبل بلد باشند و همه چی از صفر توضیح داده شده است، به همین علت، تمامی دانشجویان با هر پایه و سطحی که دارند می‌توانند از این فیلم بیشترین بهره را ببرند، حتی دانشجویانی که رشته لیسانس شان کامپیوتر نبوده است براحتی می‌توانند از این فیلم استفاده کنند و درس مدار منطقی را بصورت عمیق و مفهومی فرا گیرند.
حتما نیاز است که علاوه بر فیلم درس، فیلم‌های حل تست مدار منطقی را نیز تهیه کنید. حتی اگر نمی‌توانید فیلم درس مدار منطقی را تهیه کنید و می‌خواهید خودتان منطقی را مطالعه کنید ولی حتما سعی کنید فیلم نکته و تست منطقی را تهیه کنید.
در نکته و تست مدار منطقی سعی شده که تست ها با روش های سریع و ابتکاری حل شود که علاوه بر اینکه بتوانید این درس را 100 بزنید بتوانید در تایم بسیار کمی به تمامی تست های مدار منطقی پاسخ دهید. برای اینکه بتوانید مدار منطقی را 100 بزنید حتما باید با دقت کافی این فیلم ها را تماشا کنید. هر سال داوطلبان زیادی با استفاده از این فیلم مدار منطقی را صد زده اند. در نکته و تست مدار منطقی حدود 340 تست کنکور ارشد کامپیوتر و همین طور کنکور دکتری بطور کامل بررسی شده است، تمامی تست های کنکور از 28 سال پیش تا کنون بررسی شده و تست ای وجود ندارد که در این فیلم بررسی نشده باشد. در این فیلم تمامی مطالب چندین بار مرور و همه مطالب دسته بندی شده است
رامین رضوی
RAMIN RAZAVI
ایشان تا قبل از سال 94 بصورت حضوری در شهر تهران و بصورت پروازی در شهرهای مشهد، شیراز، اصفهان، گرگان و ... برای کنکور مقطع ارشد و دکتری تدریس می‌کرده‌اند، سپس در سال 94 با توجه به درخواست‌های مکررِ شهرهای دیگر برای برگزاری کلاس‌های آمادگی کنکور ارشد و دکتری تصمیم گرفت در جهت رفع کمبود امکانات آموزشی در شهرهای کوچک، برای اولین بار در کشور اقدام به برگزاری دوره‌های آموزشی آنلاین کند که ماحصل آن برقراری عدالت آموزشی طی این سال‌ها و شرکت بیش از 24000 دانش‌پژوه در کلاس‌های آنلاین ایشان و برگزاری 267 دوره آنلاین توسط ایشان بوده است.
در حال حاضر بیش از 90 درصد از رتبه‌های برتر کنکور ارشد کامپیوتر و آیتی هر سال از دانشجویان استاد رضوی هستند که این درصد موفقیت نه تنها در رشته کامپیوتر بلکه در هیچ رشته دیگری وجود نداشته است.
سرفصل‌های دوره مدار منطقی
برای درس مدار منطقی دو فیلم زیر وجود دارد:
- فیلم درس مدار منطقی
- فیلم حل تست سوالات مدار منطقی
ویدیو درس مدار منطقی
تخفیف زمانی تا ۲۵ تیر
30%ویدیو نکته و تست مدار منطقی
تخفیف زمانی تا ۲۵ تیر
30%در زیر سرفصل‌های دوره مدار منطقی با جزئیات آورده شده است، در زیر مشخص شده است که فیلم آموزش مدار منطقی چند جلسه است و هر جلسه چند ساعت است و شامل چه بخش‌ها و مباحثی است:
بخش 1
1:10'معرفی اعداد بی‌علامت - تبدیل مبناها - تصاعد هندسی
بخش 2
1:10'ادامه تبدیل مبناها - نمایش اعداد علامت‌دار
بخش 1
1:15'شروع اعداد علامت‌دار - سیستم مکمل 1 - سیستم مکمل 2 - مکمل در مبنای r
بخش 2
2:05'کدهای رقمی (BCD) - کدهای وزن‌دار - تفریق بی‌علامت (تفریق با تبدیل به جمع و تفریق مستقیم) - کد خود مکمل - صحبت در مورد Half Adder و Full Adder
بخش 1
1:05'جمع دو عدد BCD - مدار جمع‌کننده BCD
بخش 2
1:25'تفریق‌کننده یک رقمی BCD - تفریق‌کننده یک رقمی ex3 - جمع ex3 - جبر بول - دوگان تابع
بخش 3
1:30'اصل Duality - خواص جبر بول
بخش 1
1:15'انواع نحوه نمایش یک تابع - تعریف مینترم و ماکسترم
بخش 2
1:15'ادامه نکات ماکسترم و مینترم‌ها - پیچیدگی مدار یا Gate Input
بخش 1
1:00'تعریف گیت - پیاده‌سازی تابع به صورت تمام NAND - پیاده‌سازی تابع به صورت تمام NOR
بخش 2
1:20'خواص XOR و XNOR
بخش 3
1:10'کامل بودن توابع یا یکسری گیت - مجموعه گیت‌های کامل - بافر سه حالته
بخش 1
1:30'نکاتی در مورد XOR - جدول کارنو
بخش 2
1:45'جدول کارنو 5 متغیره - حالات بی‌اهمیت (Don’t Care) - ایجاب کننده (Implicant) - ایجاب‌کننده اولیه (Prime Implicant) - ایجاب‌کننده اولیه ضروری (Essential Prime Implicant)
بخش 1
1:35'تاخیر انتشار - مخاطره یا هازارد - انواع هازارد - مخاطره ایستا سطح 1 - مخاطره ایستا سطح 0
بخش 2
1:15'شروع مدارات ترکیبی - Half Adder - Full Adder - ساخت FA با استفاده از HA - Half Subtractor - Full Subtractor - مقایسه‌کننده
بخش 1
1:25'ادمه مقایسه‌کننده - معرفی دیکدر
بخش 2
1:40'بررسی یک دیکدر با پایه‌های خروجی active low - تحقق توابع با استفاده از دیکدر - رمزگذار یا Encoder
بخش 3
00:15'انکدر اولویت‌دار
بخش 1
1:25'در چه حالت‌هایی در خروجی مدارات، don’t care قرار می‌دهیم؟ - معرفی مالتی پلکسر(MUX) - ساخت مالتی پلکسر - پیاده‌سازی توابع با مالتی پلکسر
بخش 2
1:45'ادامه پیاده‌سازی توابع با مالتی پلکسر - دی مالتی پلکسر (demux) - قطعات منطقی برنامه‌پذیر (PLD) - معرفی ROM
بخش 1
1:00'آرایه منطقی برنامه‌پذیر(PLA) - آرایه برنامه‌پذیر منطقی (PAL)
بخش 2
1:35'شروع مدارات ترتیبی - معرفی لچ (Latch) - معرفی فلیپ‌فلاپ - انواع فلیپ‌فلاپ‌ها
بخش 3
1:25'تحلیل مدارات ترتیبی - دیاگرام حالت - جدول حالت
بخش 1
1:35'معرفی مدارات میلی و مور - تبدیل میلی به مور - تبدیل مور به میلی
بخش 2
1:35'مدارات آسنکرون - شمارنده آسنکرون - انواع شمارنده‌های سنکرون
بخش 1
1:20'مداراتی که با استفاده از آنها سیگنال زمانی ساخته میشود: شمارنده حلقوی - شمارنده جانسون
بخش 2
1:40'شروع طراحی مدارات ترتیبی - طراحی مدارات ترتیبی با استفاده از فلیپ‌های D , T, SR , JK - Sequence Detector
بخش 3
00:25'ادامه طراحی Sequence Detector
بخش 1
2:20'پارامتر های زمانی فلیپ فلاپ ها (تاخیر انتشار - تاخیر راه‌اندازی - زمان نگهداری) - کاهش حالات در مدارات ترتیبی، در جداول فاقد don’t care و در جداول دارای don’t care
بخش 1
00:50'ساده‌سازی توابع - هازارد یا مخاطره
بخش 2
1:10'ادامه ساده‌سازی توابع - از بین بردن هازارد
بخش 3
1:50'ادامه ساده‌سازی توابع - از بین بردن هازارد - معرفی گیت‌های عبور - پالس کوتاه ناخواسته (glitch)
بخش 4
00:45'از بین بردن هازارد
بخش 1
2:05'پالس ناخواسته (glitch) - معرفی nMOS و pMOS - به دست آوردن تعداد PI و EPI ها - از بین بردن هازارد
بخش 2
2:15'به دست آوردن تعداد PI و EPI ها - از بین بردن هازارد - حداقل تعداد گیت برای پیاده‌سازی تابع به صورت Hazard Free - در چه صورت در خروجی مدار، don’t care قرار می دهیم؟
بخش 1
1:45'شروع فصل 2 - تحلیل مدارات ترکیبی - طراحی دیکدر - PAL
بخش 2
1:50'مدار جمع‌کننده Ex-3 - تحلیل مدارات ترکیبی - PLA - ساخت گیت Nor با تکنولوژی NMOS
بخش 3
00:30'تحلیل مدارات ترکیبی - مدار جمع کننده BCD - PLA - ROM
بخش 1
1:05'تحلیل مدارات ترکیبی - مدارات Bit Slice
بخش 2
2:00'تحلیل مدارات ترکیبی - پیاده‌سازی یک تابع با استفاده از ROM
بخش 1
2:15'شروع فصل 3 - تحلیل شمارنده‌ها - Sequence detector - تحلیل دیاگرام حالت - به دست آوردن معادلات ورودی فلیپ فلاپ‌ها
بخش 2
00:30'Sequence detector - به دست آوردن معادلات ورودی فلیپ فلاپ‌ها
بخش 3
1:05'کاهش حالات - به دست آوردن معادلات ورودی فلیپ فلاپ‌ها - تحلیل مدارات ترتیبی
بخش 4
1:30'به دست آوردن معادلات ورودی فلیپ فلاپ‌ها - تحلیل مدارات ترتیبی - پارامترهای زمانی فلیپ فلاپ‌ها - طراحی Sequence detector
بخش 1
1:50'تحلیل مدارات ترتیبی - شمارنده جانسون - تبدیل میلی به مور - تحلیل شکل موج خروجی مدارات ترتیبی
بخش 2
2:15'تحلیل مدارات ترتیبی - کاهش حالات - Sequence detector
بخش 1
00:50'سال 91: گیت‌های Open Collector - منطق کامل
بخش 2
1:10'بررسی فلیپ فلاپ SR - پیاده‌سازی تابع با حداقل گیت - تحلیل دیاگرام حالت - FA و HA - به دست آوردن تعداد EPI
بخش 3
00:40'مدار دوبرابرکننده فرکانس - تحلیل مدارات ترتیبی و ترکیبی
بخش 4
1:00'سال 92: Gate Input - گیت‌های Open Collector - پارامترهای زمانی فلیپ فلاپ‌ها - رفع هازارد - بررسی شکل موج خروجی مدارها
بخش 5
00:40'اندازه ROM لازم برای پیاده‌سازی تابع - مدار Ring Oscillator
بخش 6
00:45'تحلیل دیاگرام حالت - بررسی هازارد - فلیپ فلاپ‌های Master-Slave
بخش 7
2:05'سوئیچ دارای Bounce - بررسی شکل موج خروجی مدارات - سال 93: گیت NOR از نوع Open Collector - بررسی هازارد - پارامترهای زمانی فلیپ فلاپ‌ها - پیاده‌سازی مدار ترکیبی با استفاده از FA و HA - طراحی Sequence detector - ساخت شمارنده آسنکرون
بخش 8
2:00'تبدیل مبنا - Gate Input - سال 94: glitch - تحلیل دیاگرام حالت - PAL - مدار شمارنده صعودی آسنکرون - تابع Majority - Wired-OR و Wired-AND - Reduction OR و Bitwise OR
بخش 9
2:20'سال 95: رفع هازارد - گیت سه وضعیتی (tri-state) - سال 97: کاهش حالات - بررسی هازارد - پیاده‌سازی بدون مخاطره توابع - تعداد PI , EPIها
بخش 1
1:05'ادامه سوال‌های فصل 3 - تحلیل مدارات ترتیبی - تحلیل دیاگرام حالت
بخش 2
00:50'تحلیل شکل موج خروجی مدارات ترتیبی - کاهش حالات
بخش 3
1:50'تحلیل دیاگرام حالت - تحلیل مدارات ترکیبی
بخش 1
1:40'تبدیل مبناها - مکمل 9 - کد BCD - کدهای وزن‌دار - فاصله همینگ
بخش 2
1:00'تبدیل کد باینری به گری و بالعکس - تفریق Ex-3 - منطق کامل - منطق منفی - Gate Input
بخش 1
1:40'مسابقه ( Race) - مسابقه بحرانی و غیربحرانی در مدارترتیبی - مسابقه بحرانی و غیربحرانی در مدارترکیبی - ورودی ممنوعه - مدارات ترتیبی آسنکرون - فیدبک - تحلیل مدار ترتیبی آسنکرون مد پایه - حالت پایدار و ناپایدار
بخش 2
00:50'محدودیت‌های مد پایه - سوالات حالات پایدار و ناپایدار - شروع زبان Verilog
بخش 3
1:00'انواع توصیف‌ها در زبان Verilog - ویژگی توصیف‌های مختلف - توضیح initial و always - تستهای Verilog - glitch
بخش 4
00:45'تحلیل دیاگرام حالت - Sequence detector - ROM
بخش 1
1:05'تحلیل مدار Carry Lookahead Adder - پارامترهای زمانی فلیپ فلاپ‌ها - تحلیل کد Verilog
پی دی اف (pdf) درس مدار منطقی
هر یک از فیلم‌های درس یا حل تست مدار منطقی را تهیه کنید در داشبورد پی دی اف مربوط به آن دوره نیز قرار می‌گیرد و دانشجویان براحتی می‌توانند جزوات را پرینت و هنگام تماشای فیلم‌های درس و حل تست منطقی از جزوات خط ببرند و مطالب مهم را هایلایت کنند و در صورن نیاز برای خودتان در کنار جزوات یاداشت برداری کنید. همچنین در سایت کنکور کامپیوتر میتوانید به معتبرترین جزوات درس مدار منطقی که در بهترین دانشگاههای ایران تدریس شده به صورت کاملا رایگان و در قالب pdf دسترسی داشته باشید
فیلم‌های رایگان
مدار منطقی چیست؟
مدارهای منطقی (Logic Circuit)، مدارهایی هستند که کامپیوترها از آنها ساخته می‌شوند. امروزه درک صحیحی از مدارهای منطقی برای هر مهندس برق و کامپیوتر ضروری است. این مدارها عنصر اصلی کامپیوترها و بسیاری از وسایل دیگر نظیر: دستگاه‌های ضبط و پخش موسیقی و تصویر، بازی‌های الکترونیک، ساعت‌های دیجیتال، دوربین‌های فیلمبرداری، گیرنده‌های تلویزیون، چاپگرها و بسیاری از لوازم خانگی و همچنین در سیستمهای بزرگ مانند شبکه‌های تلفن، تجهیزات اینترنت و ... هستند. مشخص است که مدارهای منطقی یکی از اجزای بسیار مهم در زندگی امروزی ما محسوب می‌شوند. هدف درس مدار منطقی آشنا کردن شما با فرایند طراحی مدارهای منطقی است. روند آموزش در درس مدار منطقی به اینصورت است که ابتدا ایده‌های کلیدی و عناصر پایه‌ی مدارهای منطقی با مثال‌های ساده تشریح میشود، سپس آموزش داده میشود که چگونه میتوان با این عناصر پایه مدارهای بسیار پیچیده خلق کرد. مدارهای منطقی روی تراشه‌های نیمه‌رسانا و با استفاده از ترانزیستور و سایر عناصر الکترونیکی پیاده‌سازی میشود. اغلب تراشه‌های امروزی (از جمله پردازنده‌های کامپیوتری) بیش از یک میلیارد ترانزیستور دارند.
کتاب های مرجع درس مدار منطقی چه هستند؟
مرجع اصلی که برای درس مدار منطقی در دانشگاههای معتبر تدریس میشود کتابهای موریس مانو و نلسون است، همچنین کتابهای هریس (Harris) و براون (Brown) نیز در برخی از دانشگاههای ایران و جهان تدریس میشود، در این صفحه میتوانید بصورت رایگان کتاب های مرجع مدار منطقی را براحتی دانلود و از آنها استفاده کنید.
درس مدار منطقی شامل چه مباحث و فصولی است؟
رئوس مطالبی که در درس مدار منطقی وجود دارد عبارت است از: سیستمهای نمایش مختلفی که برای نمایش اعداد در کامپیوتر وجود دارد، جبر بول، ساده سازی توابع منطقی، ایجاب کننده و PI و EPI، مخاطره و هازارد، مدارات ترکیبی، تحلیل مدارات ترتیبی، طراحی مدارات ترتیبی، کاهش حالات
درس مدار منطقی چقدر در کنکور ارشد کامپیوتر اهمیت دارد؟
با توجه به ساده بودن و امن بودن درس مدار منطقی و اینکه دانشجویان می‌توانند به 100 درصد سوالات درس مدار منطقی پاسخ دهند درس مدار منطقی مهم ترین درس کنکور ارشد کامپیوتر محسوب میشود و به تمامی داوطلبان کنکور ارشد کامپیوتر توصیه میشود که این درس را مطالعه کنند و به هیچ عنوان درس مدار منطقی را کنار نگذارند
از درس مدار منطقی چند تست در کنکور ارشد کامپیوتر مطرح میشود؟
در کنکور ارشد کامپیوتر 99 از درس مدار منطقی 12 تست مطرح شد، اما با توجه به تغییرات به وجود آمده در کنکور ارشد کامپیوتر هنوز مشخص نیست که در کنکور ارشد کامپیوتر 1400 چند تست از درس مدار منطقی مطرح میشود ولی حدس ما این است که 10 تست از این درس در کنکور ارشد کامپیوتر 1400 مطرح شود
ضریب درس مدار منطقی در گرایش های مختلف کنکور ارشد کامپیوتر چیست؟
ضریب درس مدار منطقی در گرایش معماری کامپیوتر دارای ضریب ۴ و در گرایش های شبکه های کامپیوتری، رایانش امن، نرم افزار، بیوانفورماتیک، علوم داده، الگوریتم و محاسبات و علوم و فناوری شبکه دارای ضریب 3 و در گرایش های هوش مصنوعی و قرآن کاوی رایانشی دارای ضریب 2 است.
ساجده فدائی 
کیان انواری 
علیرضا بهدوست 
احسان داستانی 
معین منعمی 
علیرضا حسن زاده باقی 
سعيد نوروزيان 
بهمن قائدی 
مهدی مزارعی 
سینا مهرآبادی 
محمد امین شنابی 
سارا مختاری همامی 
Amir hossein 
emelkabi 
محمد چاروسایی 
علیرضا ملکی 
علی فتحی وافق 
غزل موسوی 
انوش مه جبین 
سعید راصدی 
یوسف عباسی 
مهدی حسنی 
احمد بنائیان 
فاطمه سادات لطفی فاطمی 
محمد رضا کمالی 
پریسا نکوگل 
حسین پری نور 
محسن سروری 
فاطمه اکبرنژاد 
علی بابایی 
مجید محمددوست 
هانیه طالبی 
اسما سهرابی 
