برای شروع حرفهای کنکور ارشد کامپیوتر،آیتی و علوم کامپیوتر حتما روی عکس زیر کلیک کنید تا در کانال کنکور کامپیوتر عضو شوید، در این کانال به معرفی بهترین منابع کنکور ارشد،برنامه ریزی و مشاوره، معرفی گرایشها و هر آنچه برای موفقیت در کنکور ارشد نیاز دارید پرداخته شده است

ریاضیات گسسته از جمله دانشهایی محسوب میشود که پایه بسیاری از علوم دیگر را شکل میدهد. به زبان ساده میتوان گفت که ریاضیات گسسته، زبانِ ریاضیِ علوم کامپیوتر است؛ به همین دلیل اهمیت آن در دهههای اخیر به طور چشمگیری افزایش یافته است. به عنوان مثال الگوریتم های کامپیوتری، زبانهای برنامه نویسی، رمز نگاری و توسعه نرم افزارها از طریق ریاضیات گسسته قابل انجام خواهند بود. در این مقاله 11 کاربرد اساسی ریاضی گسسته در علوم کامپیوتر را شرح خواهیم داد. با ما همراه باشید.
ریاضی گسسته چیست؟
ریاضیات گسسته یا Discrete Mathematics شاخهای از علم ریاضیات است که به مطالعه عناصر گسسته و مجزا میپردازد. دانش ریاضی گسسته نقطه مقابل ریاضیات پیوسته (مانند حساب دیفرانسیل و انتگرال) است. اين شاخه از علم رياضی به مطالعه چگونگی ترکیب اجزاء گسسته و احتمالات مختلف در نتایج آن میپردازد. از دیگر مواردی که در ریاضیات گسسته به آنها پرداخته میشود میتوان به شمارش، تبدیل(جایگشت)، ترکیب، نظریه گراف، نظریه اعداد، مجموعهها و روابط، تابع و رابطه بازگشتی اشاره کرد.
از ریاضیات گسسته برای طراحی الگوریتم های کامپیوتری، در برنامه نویسی (Programming) به زبان های مختلف و در دنیای ملموس پیرامون مانند تنظیم برنامه حرکت قطارها، Google Maps، سیستم های رأی گیری و بسیاری از کاربردهای دیگر مورد استفاده قرار می گیرد.
اهمیت ریاضیات گسسته در علوم کامپیوتر
دستیابی به دانشهای کاربردی در علوم کامپیوتر، مستلزم یادگیری مفاهیم ریاضی مرتبط با آن است. به بیان دیگر ریاضیات مانند پلی است که علوم کامپیوتر را از مرحله تئوری به مرحله عملی میرساند. دانستن علم ریاضیات گسسته موجب میشود متخصصان علوم کامپیوتر به درک عمیقتری از مفاهیم کامپیوتری برسند و همچنین به کمک کامپیوتر بتوانند انجام بسیاری از امور روزمره را ساده کنند. به همین دلیل است که دانش آموزان و همین طور دانشجویان رشته کامپیوتر لازم است در مقاطع تحصیلی مختلف، به مطالعه ریاضیات گسسته بپردازند تا در ابتدا با مفاهیم کلی آن و در آینده با کارکردها و کاربردهای کامپیوتری آن آشنا شوند.
کاربردهای ریاضی گسسته در علوم کامپیوتر
لیست زیر کاربرد بخشهای مختلف ریاضیات گسسته در علوم کامپیوتر را بیان میکند که در ادامه هر یک از این موارد را توضیح خواهیم داد
- تئوری محاسبات
- تئوری اطلاعات
- رمزنگاری
- پایگاه داده رابطه ای
- برنامه نویسی
- سیستم عامل
- الگوریتم های کامپیوتری
- تئوری گراف
- نظریه احتمال گسسته
- هندسه محاسباتی و هندسه گسسته
- درخت ها
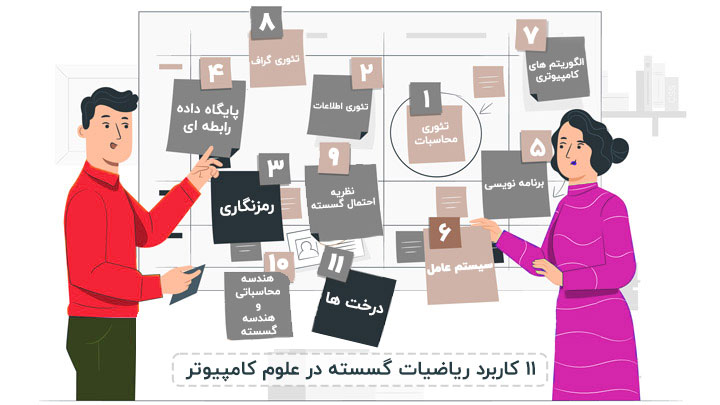
کاربردهای 11 گانه ریاضی گسسته در علم کامپیوتر
1- نظریه محاسبات (Theory of Computation)
نظریه محاسبه شاخهای از علوم کامپیوتر و ریاضیات گسسته است که به بررسی موارد گوناگونی میپردازد، از جمله مسائلی که نظریه محاسبه به بررسی آن میپردازد این است که قابلیتها و محدودیتهای کامپیوتر چیست؟
در واقع به بررسی این موضوع میپردازد که کامپیوترها توانایی انجام چه کارهایی را دارند و چه کارهایی را نمیتوانند انجام دهند. برای بررسی این موضوع باید کامپیوترها را مدل کنیم، یک مدل محاسباتی نحوه سازماندهی واحدهای محاسباتی، حافظهها و ارتباطات را توصیف میکند. پیچیدگی محاسباتی یک الگوریتم را میتوان با توجه به این مدل های محاسباتی اندازه گیری کرد. استفاده از مدلهای محاسباتی امکان مطالعهِ عملکرد الگوریتمها را (مستقل از تغییراتی که مخصوص پیادهسازیهای خاص و فناوریهای خاص هستند) به ما میدهد. دو مورد از مدلهای معروفی که در این زمینه وجود دارند Finite state machines و Turing machines ماشین است. حال که با مفهوم مدل محاسباتی بیشتر آشنا شدید میتوانیم بطور دقیق تر بگوییم که نظریه محاسباتی چه چیزهایی را بررسی میکند.
نظریه یا تئوری محاسبات در مورد یک مسئله موارد زیر را بررسی میکند:
- این مسئله را روی کدامیک از مدلهای محاسباتی میتوان حل کرد؟
- این مسئله را با استفاده از چه الگوریتمهایی میتوانیم حل کنیم؟
- این مسئله را تا چه حد کارآمد (efficiently) میتوان حل کرد و آن الگوریتم به چه میزان از منابع محاسباتی سیستم ما استفاده میکند؟
- پیچدگی محاسباتی و درجه الگوریمتی که برای مسئله ارائه میدهیم حداقل به چه میزان میتوان باشد؟ در واقع بررسی میشود که چقدر توانایی بهتر حل کردن یک مسئله وجود دارد، این مسئله یکی از زیر شاخههای نظریه محاسبه است که به نام نظریه پیچیدگی (computational complexity theory) شناخته میشود.
- آیا میتوان برای یک مسئله راه حل دقیقی ارائه کرد یا باید از راه حلهای تقریبی برای آن استفاده کرد؟
بطور کلی شاخه نظریه محاسبه از دل ریاضیات گسسته برآمده است.
2- تئوری اطلاعات (Information Theory)
نظریه یا تئوری اطلاعات (Information theory)، به مقداردهی (Quantification)، ذخیره سازی و انتقال اطلاعات میپردازد. این رشته اساساً با کارهای هری نایکیست و رالف هارتلی در دهه 1920 و کلود شانون در دهه 1940 تأسیس شد. نظریه اطلاعات مبتنی بر نظریه احتمال و آمار است و نظریه احتمال و آمار زیر مجموعه ریاضیات گسسته محسوب میشود.

نظریه اطلاعات اغلب به اندازه گیری اطلاعات توزیعهای مرتبط با متغیرهای تصادفی مربوط می شود. مقادیر مهم اطلاعات عبارتند از آنتروپی (entropy)، اندازه گیری اطلاعات یک متغیر تصادفی و اندازه گیری اطلاعات مشترک بین دو متغیر تصادفی.
زیرشاخه های مهم تئوری اطلاعات عبارتند از: کدگذاری منبع (source coding)، نظریه پیچیدگی الگوریتمی(algorithmic complexity theory)، نظریه اطلاعات الگوریتمی (algorithmic information theory) و امنیت تئوریک اطلاعات (information-theoretic security) است.
هربار که یک فایل را در فرمت ZIP یا RAR فشرده میکنید و یا یک موسیقی را در قالب mp3 گوش میدهید، در حال استفاده از دستاوردهای نظریه اطلاعات هستید.
برخی از مواردی که از تئوری اطلاعات باعث به وجود آمدن آنها شده است :
- فشرده سازی داده ها (مثلاً برای فایل های ZIP)
- تشخیص و تصحیح خطا در ارسال بستههای داده در شبکه های کامپیوتری
- تاثیر آن در موفقیت ماموریتهای کاوشگر رباتیک وویجر به اعماق فضا
- اختراع لوح فشرده
- ایجاد تلفن های همراه
- توسعه اینترنت
همچنین این نظریه در زمینههای زیر نیز کاربرد پیدا کرده است
- رمزنگاری
- عصب شناسی (neurobiology)
- زبانشناسی (linguistics)
- بیوانفورماتیک (bioinformatics)
- فیزیک حرارتی (thermal physics)
- دینامیک مولکولی (molecular dynamics)
- محاسبات کوانتومی (quantum computing)
- بازیابی اطلاعات (information retrieval)
- تشخیص سرقت ادبی (plagiarism detection)
- تشخیص الگو (pattern recognition)
- ایجاد آثار هنری (art creation)
رمزنگاری (Cryptography)
رمزنگاری دانشی است که به بررسی و مطالعه تکنیکهایی برای برقراری ارتباط و انتقال یا ذخیره اطلاعات به صورت امن، حتی اگر مسیر انتقال اطلاعات و کانالهای ارتباطی یا محل ذخیره اطلاعات ناامن باشند میپردازد. به بیانی دیگر رمزنگاری در مورد ساخت و تجزیه و تحلیل پروتکلهایی است که از خواندن پیام های خصوصی توسط اشخاص ثالث یا عموم جلوگیری میکند.

رمزنگاری از اهمیت بالایی در تامین اهمیت مسیرهای داده برخوردار است
در رمزنگاری مدرن جنبههای مختلف زیر برای امنیت اطلاعات مهم هستند:
- محرمانه بودن داده ها یا محرمانگی (confidentiality) : فقط ارسال کننده و گیرنده مورد نظر باید بتوانند محتوای پیام ارسالی را بفهمند. بنابراین فرستنده باید دادههایی که قرار است به سمت مقصد ارسال شود را قبل از ارسال روی شبکه رمزنگاری کند
- صحت داده یا پیام (data integrity): فرستنده و گیرنده باید مطمئن شوند که محتوای پیامهای ارسالی و دریافتی آنها چه تصادفی و چه عمدا دچار تغییر نخواهد شد
- end-point authentication: باید مطمئن شویم که فردی یا سیستمی که داریم با آن ارتباط برقرار میکنیم واقعا همانی است که انتظار داریم و فردی یا سیستم دیگری خود را به جای فرد یا سیستم مورد انتظار ما جا نزده باشد. باید مطمئن شویم که آیا آن کسی که ما داریم با آن ارتباط برقرار میکنیم، واقعا همانی هست که انتظار داریم
از کاربردهای رمزنگاری می توان به تجارت الکترونیک، کارت های پرداخت مبتنی بر تراشه (chip-based payment cards)، ارزهای دیجیتال، رمزهای عبور رایانه و ارتباطات نظامی اشاره کرد.
در تعریف ارز دیجیتال یا کریپتوکارنسی می توان گفت نوعی دارایی رمزنگاری شده مجازی است که احتمال هرگونه تقلب و کلاهبرداری در تراکنش های آن صفر است. غالب رمز ارزها بر بستر شبکه بلاک چین (Blockchain) و بصورت شبکه هایی غیر متمرکز ایجاد شده اند.
معمولاً ارزهای دیجیتال نمی توانند تحت دستکاری هیچ سازمان یا مرجع قانونی قرار بگیرند و این عدم دسترسی دولت ها به تراکنش های شبکه بلاک چین یکی از بارزترین مزایای رمز ارزهاست.
حال که با مفهوم رمزنگاری آشنا و موارد کاربرد آن آشنا شدیم بیاید به بررسی جایگاه ریاضی گسسته در آن بپردازیم.
نظریه یا همان تئوری اعداد که یکی از بخشهای ریاضی گسسته محسوب میشود کاربردهای مهمی در بلاکچین، رمزنگاری و امنیت رایانه دارد.
به عنوان مثال یکی از جنبههای کاربرد نظریه اعداد در رمزنگاری، استفاده از اعداد اول و خواص آن است، به این صورت که ما از گذشته میدانستیم که همه اعداد را میتوان به عوامل اولشان تجزیه کرد، برای مثال عدد ۳۸۵ را میتوان از ضرب سه عدد ۵ در ۷ در ۱۱ که همگی عدد اول هستند به دست آورد. این موضوع در مورد اعداد بزرگتر نیز صادق است، برای مثال میتوان عدد ۳۴۷۴۲۳۹۳۰ را با ضرب کردن اعداد ۲ در ۵ در ۷ در ۱۹ در ۹۷ در ۲۶۹۳ به دست آورد.
نکته اصلی اینجاست که اگر از بهترین الگوریتم موجود به منظور تقسیم یک عدد ۱۰۰۰ رقمی یا ۲۰۰۰ رقمی به فاکتورهای اول آن استفاده کنیم، بهترین سوپرکامپیوتر موجود نیز به زمان بسیار بسیار زیادی برای اتمام کار خود نیاز خواهد داشت؛(شايد چندين برابر عمر کره زمين!) پس به زبان ساده، محدودیتی برای پیدا کردن فاکتورهای اول یک عدد وجود دارد و این موضوع برای امنیت در رایانههای مدرن بسیار حیاتی و ضروری است.
در اين الگوریتم رمزنگاری با استفاده از دو عدد اول بزرگ حاصلضرب آنها را که یک عدد خیلی بزرگ است پیدا میکنند و با استفاده از این عدد خیلی بزرگ عملیات رمزگذاری پیام شروع میشود. حال اگر بخواهیم پیام رمزشده (encrypted) را رمزگشایی (decrypted) کنیم به آن دو عدد اولی که با آن، عدد خیلی بزرگ تولید شده است نیاز داریم. روش ذکر شده، از مراحل رمز کردن متن با استفاده از الگوریتم RSA است که معمولیترین الگوریتمیست که در شیوه رمزنگاری نامتقارن (Asymmetric cryptography) از آن استفاده میشود.
سیستمهای رمزنگاری مدرن باید از نظر ریاضی صحیح، قوی و قابل اعتماد باشند تا دادههای کاربران را در برابر دشمنان ایمن کنند. به دلیل بالا بودن ارزش، هزینه و محرمانگی برخی اطلاعات، رمزنگاران بهتر است پیشینهای قوی در تئوری اعداد داشته باشند تا بتوانند ایمنی سیستمها و رمزهای عبور را تضمین کنند.
دانستن تکنیکهای شمارش، که شاخهای دیگر از ریاضیات گسسته محسوب میشود، نیز میتواند یک شهود و دید کلی به ما در تعیین تعداد رمزهای عبور معتبری که از مجموعه قوانین مشخصی پیروی میکنند، بدهد تا از نفوذ مجرمانی که قصد شکستن رمز را دارند به وسیلهی طولانی کردن مدت زمان بررسی احتمالات گوناگون، جلوگیری کند.
شما میتوانید زمان لازم برای شکستن پسورد خود را در این سایت مشاهده کنید.
4- پایگاه داده رابطهای (Relational Database)
پایگاه داده رابطهای نوعی پایگاه داده براساس مدل رابطهای دادههاست. در این مدل، دادهها در قالب تعدادی جدول (Table) نگهداری میشوند. به این جداول، رابطه (Relation) نیز گفته میشود. هر جدول شامل تعدادی ستون (Column) و ردیف (Row) میباشد. به ستونها، ویژگی (Attribute) و به ردیفها رکورد (Record) یا چندتایی (تاپل یا Tuple ) نیز گفته میشود.
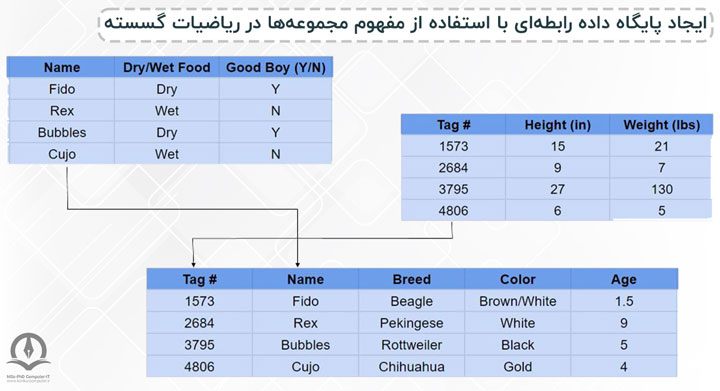
جداول داده در مدل رابطه ای
یک پایگاه داده رابطهای ویژگیهای یک قطعه خاص از اطلاعات را به هم متصل میکند. به عنوان مثال، در یک پایگاه داده حاوی اطلاعات مشتری، جنبه رابطه ای این پایگاه داده به سیستم کامپیوتری اجازه می دهد تا بداند نام، آدرس، شماره تلفن و سایر اطلاعات مربوط به مشتری را چگونه پیوند دهد. موارد ذکر شده از طریق مفهوم مجموعهها در ریاضیات گسسته انجام میشوند؛ مجموعه ها اجازه میدهند اطلاعات گروه بندی و مرتب شوند. از آنجایی که هر بخش از اطلاعات و هر صفت متعلق به آن قطعه اطلاعات گسسته است، سازماندهی چنین اطلاعاتی در یک پایگاه داده نیازمند روش های ریاضی گسسته است.
5- برنامه نویسی (Programming)
ریاضیات گسسته به ایجاد رویکردی منطقی برای حل یک مسئله کمک میکند و مهارت کافی در این زمینه برای برنامه نویسان بسیار مهم است زیرا درک مفاهیم آن به برنامه نویسان کمک خواهد کرد که کدها و الگوریتم های بهتری را ارائه دهند. الگوریتمها با این دید طراحی میشوند که بعد از تبدیل به یک زبان برنامه نویسی مانند Python، Java یا C، برای اجرا به کامپیوتر داده شوند.

6- سیستم عامل (Operating System - OS)
در سیستم عاملها مسئله تخصیص منابع بسیار حائز اهمیت است. هر فرایند یا پردازه (Process)( به برنامه در حال اجرا فرایند گفته میشود) برای اجرای خود در کامپیوتر نیاز دارد تا از منابع (هر آنچه که یک فرایند برای شروع و ادامه اجرا به آن نیاز دارد) آن کامپیوتر مانند CPU، حافظه، دیسک، I/O و ... استفاده کند. به عنوان مثال وقتی شما از برنامه فتوشاپ استفاده میکنید، لازم است تا کدهای لازم جهت اجرای صحیح فتوشاپ از حافظه فرخوانی شده (Fetch) و توسط CPU اجرا شوند. این موضوع زمانی اهمیت پیدا میکند که کامپیوتر شما در حال اجرای چندین برنامه باشد. اگر تخصیص منابع به این فرایندها به درستی صورت نگیرد، برنامههای شما قادر نیستند به درستی اجرا شده و به صورت موثر از پردازنده استفاده کند. سیستم عامل باید با استفاده از الگوریتمهایی بتواند به هر فرایند در زمان مناسب، منابع مورد نیازش را تخصیص دهد و در زمان مناسب آن منابع را از آنها بگیرد تا هر فرایند به درستی انجام شده و تداخلی در کار آنها پیش نیاید. یکی از الگوریتمهای موثر برای حل این مسئله استفاده از گراف تخصیص منابع است.
گراف تخصیص منابع به صورت مجموعه رئوس V و مجموعه یال های جهت دار E تعریف میشود.
- دو نوع راس در این گراف وجود دارد: پردازه ها و نوع منابع
P = {P1, P2, …, Pn} مجموعه همه پردازههای سیستم
R = {R1, R2, …, Rm} مجموعه همه انواع منابع سیستم
- هر یال جهت دار نشانگر درخواست یا اختصاص منبع
درخواست منبع: P1 ➝ Rj
اختصاص منبع: Rj ➝ Pi
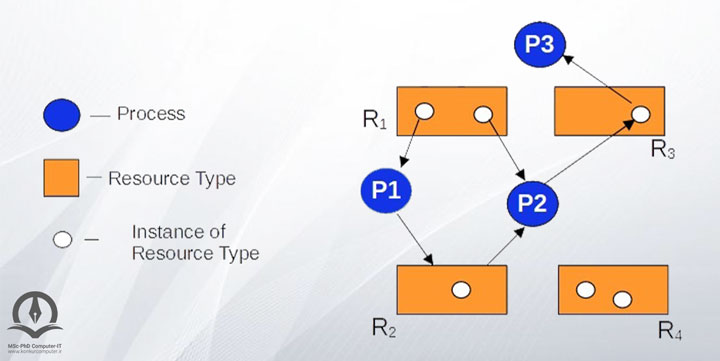
7- الگوریتمهای کامپیوتری (Computer Algorithms)
الگوریتمها، قوانینی هستند که یک کامپیوتر بر اساس آنها کار میکند. این قوانین از طریق قوانین ریاضیات گسسته ایجاد میشوند. یک برنامه نویس کامپیوتر از ریاضیات گسسته برای طراحی الگوریتمهای کارامد استفاده میکند. این طراحی شامل استفاده از ریاضیات گسسته برای تعیین تعداد مراحلی است که یک الگوریتم باید تکمیل کند، که به معنای سرعت الگوریتم است. به دلیل کاربردهای ریاضی گسسته در الگوریتمها، رایانههای امروزی سریعتر از گذشته کار میکنند.
از دیگر کابردهای ریاضیات گسسته در طراحی الگوریتم، میتوان به استفاده از نظریه گراف، که جز مباحث ریاضیات گسسته محسوب میشوند، اشاره کرد. مهمترین کاربرد گراف مدلسازی پدیدههای گوناگون و بررسی بر روی آنهاست. با گراف میتوان به راحتی یک نقشه بسیار بزرگ یا شبکهای عظیم را در درون یک ماتریس به نام ماتریس وقوع گراف ذخیره کرد یا الگوریتمهای مناسب مانند الگوریتم دایجسترا یا الگوریتم کراسکال و… را بر روی آن اعمال نمود.

دنباله فیبوناتچی کاربردهایی فراتر از تصور در علوم مختلف دارد
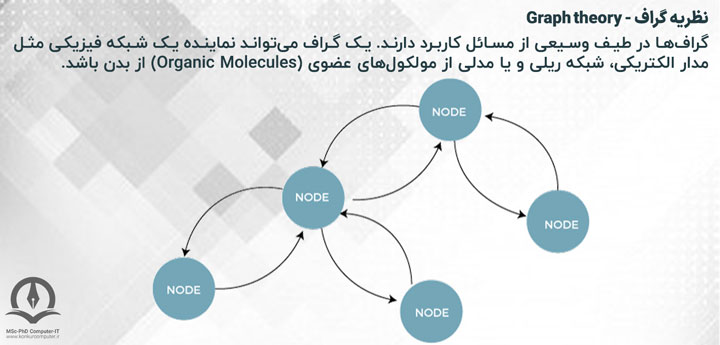
8- تئوری گراف (Graph Theory)
در علوم کامپیوتر، از گرافها برای نمایش شبکههای ارتباطی، سازماندهی دادهها، دستگاههای محاسباتی و غیره استفاده میشود.
به عنوان مثال، ساختار لینک یک وب سایت را میتوان با یک گراف جهت دار نشان داد که در آن رئوس نشان دهنده صفحات وب و یالهای جهت دار نشان دهنده لینکهایی از یک صفحه به صفحه دیگر است.
برنامه مسیریابی شما از الگوریتم جستجوی گراف برای یافتن سریعترین مسیر از خانه شما به محل کارتان استفاده میکند.
از دیگر کاربردهای آن میتوان به تجزیه و تحلیل شبکهها، تخصیص منابع در سیستم عامل و یادگیری عمیق، Functional Programming و ... اشاره کرد.
9- نظریه احتمال گسسته (Discrete Probability Theory)
نظریه احتمال گسسته به رویدادهایی میپردازد که در فضاهای نمونه قابل شمارش رخ میدهند. به عنوان مثال دسته ای از پرندگان را در نظر بگیرید. با شمارش تعداد پرندگان با کمیت گسسته سرو کار داریم؛ مثلا نمیتوان گفت دراین دسته پنج تا و نیم عدد پرنده وجود دارد. در عین حال اگر بخواهیم وزن این پرندگان را تخمین بزنیم، دادهها پیوسته خواهند بود.

از توزیعهای احتمال گسسته میتوان برای تقریب توزیع های پیوسته و بالعکس استفاده کرد. در موقعیتهای بسیار محدود مانند پرتاب تاس یا آزمایش با دستههای کارت (experiments with decks of cards)، محاسبه احتمال رویدادها اساساً شمارشی است.
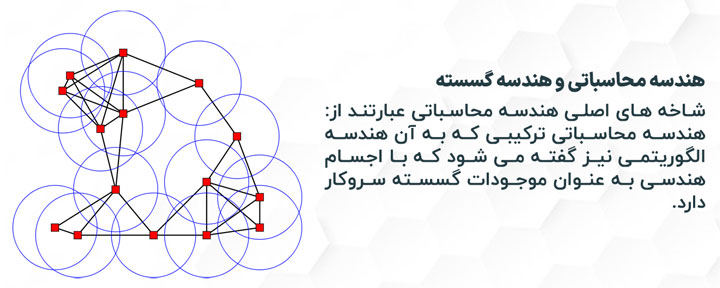
10- هندسه محاسباتی و هندسه گسسته (Computational Geometry & Discrete Geometry)
هندسه گسسته و هندسه محاسباتی(یا هندسه ترکیبیاتی) شاخههایی از هندسه هستند که ویژگیهای ترکیبیاتی اشکال هندسی گسسته را بررسی میکنند. بیشتر سوالات در هندسه گسسته شامل مجموعههای متناهی و نامتناهی از اشکال هندسی میشود؛ بهعنوان نمونه نقطه، خط، صفحه، دایره، کره، چندضلعی. هندسه گسسته بر ویژگیهای ترکیبیاتی این اشکال تمرکز میکند؛ مثلاً چگونه با یک دیگر اشتراک پیدا میکنند یا اینکه آنها چگونه میتوانند مرتب شوند تا یک شکل بزرگتر را بپوشانند.
تمام مسائل هندسی را میتوان با استفاده از الگوریتم های اعمال شده توسط هندسه محاسباتی حل کرد.
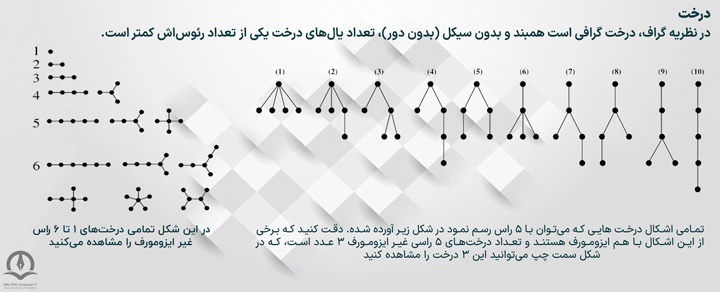
11- نمودار های درختی (Trees)
یک درخت، گرافیست همبند و بدون دور(Cycle). درخت شامل مجموعههای متناهی از عناصر به نام گره یا راس است که به وسیله خطوطی به نام یال به یکدیگر متصل میشوند. نماد شروع یک درخت به عنوان ریشه شناخته می شود و ریشه درخت نمیتواند تهی باشد.(بهتر است به این نکته توجه داشته باشید که تعریف درخت در ساختمان داده با مفهوم درخت در ریاضیات گسسته کمی تفاوت دارد.)
اگر بخواهیم نتیجه احتمالی هر آزمایشی را با درصد خطای خیلی کم، پیدا کنیم، درخت گزینه خوبی برای انجام این کار خواهد بود.
جمع بندی
ریاضیات گسسته کاربردهای فراوانی در علوم و فناوریهای مختلف دارد، علوم کامپیوتر یکی از مواردی است که به شکل مستقیم با ریاضیات گسسته در ارتباط است. ریاضی گسسته میتواند از مسیرهای گوناگونی در علوم کامپیوتر به ما کمک کند که در این مقاله به 11 مورد از این کاربردها پرداختیم. لازم به ذکر است استفاده از ریاضیات گسسته در گسترش دانش کامپیوتر تنها به این موارد محدود نمیشود و دامنه بسیار وسیعی دارد.








































