نویسنده : ساجده فدائی - دانشجو ارشد کامپیوتر صنعتی شریف شاید در اولین مواجه‌تان با نظریه گراف کمی سردرگم شوید و فکر کنید موضوعی ترسناک و نامفهوم است و از خودتان بپرسید، چرا باید وقت خودم را صرف خواندن مقاله‌ای در این مورد کنم؟ اما در پاسخ به این سوال باید گفت، اگرچه نظریه گراف برخلاف تصور اکثریت افراد چندان کارآمد نیست، اما کاربردهای مفید و مهم زیادی در علوم مختلف و یا حتی زندگی روزمره دارد! هدف این مقاله ارائه یک مقدمه جامع در رابطه با نظریه گراف است و سعی داریم شما را متقاعد کنیم که دانستن برخی از مبانی نظریه گراف تا چه میزان می‌تواند مفید و موثر باشد.
تاریخچه نظریه گراف
تئوری گراف برای اولین بار، در سال 1735 میلادی (قرن هجدهم) توسط آقای لئونارد اویلر، ریاضیدان سوئیسی ، یکی از برجسته‌ترین ریاضیدانان قرن هجدهم (یا شاید بهتر است بگوییم تمام دوران!) در رابطه با حل مسئله معروف پل کوئینزبرگ معرفی شد.
مسئله پل کوئینزبرگ، یک معمای قدیمی در مورد یافتن مسیری بر روی هفت پل تعبیه شده بر روی رودخانه شهر بود که در آن عابرین مجاز بودند تنها یک بار از روی هریک از پل‌ها عبور کنند. اویلر با در نظرگرفتن محدودیت‌ها، اولین نمایش بصری شناخته شده از یک نمودار مدرن، شامل مجموعه ای از نقاط (راس یا گره) و خطوط مابین آنها (یال) را ترسیم کرد.
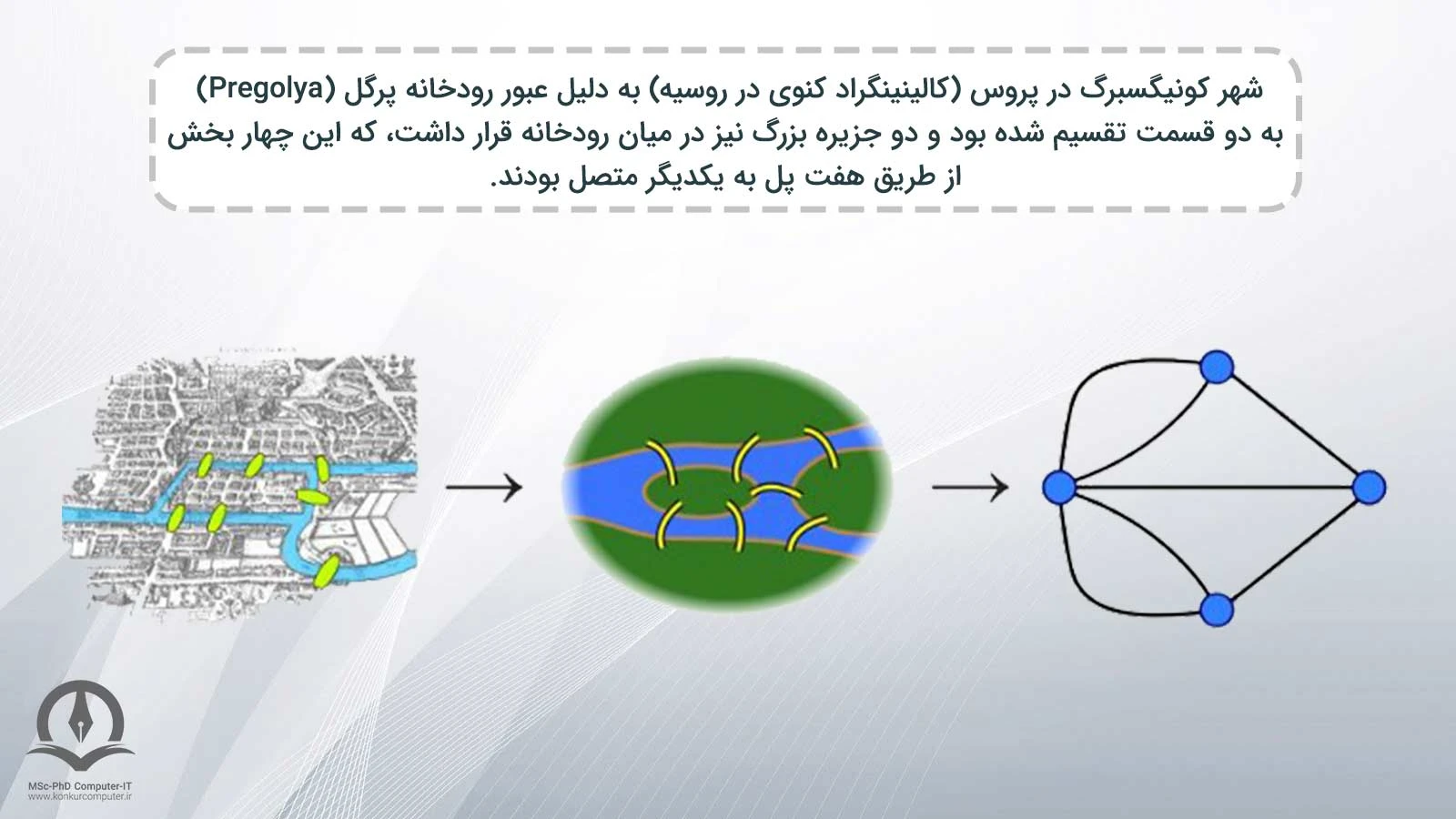
اویلر، مسئله شهر و پل‌ها را به یک نمایش انتزاعی قابل حل به زبان ریاضی درآورد و در نهایت ثابت کرد که این مسئله راه حلی ندارد. اما جواب منفی اویلر بنیان نظریه گراف را بنا کرد و ایده توپولوژی را بیش از پیش ترسیم نمود و نظریه گراف بعنوان شاخه ای از ریاضیات گسستهجامع ترین آموزش درس ریاضی گسسته
درس ریاضیات گسسته به معرفی مباحثی نظیر شمارش و احتمال، استدلال و برهان خلف، نظریه اعداد، منطق ریاضی، روابط بازگشتی، روابط و نظریه گراف می‌پردازد. از آن رو که در عصر کنونی ریاضی گسسته بطور گسترده در رشته کامپیوتر و برنامه نویسی استفاده می‌شود در این صفحه به معرفی و بررسی درس ریاضی گسسته پرداخته شده است شناخته شد.
در عصر مدرن امروزی، نظریه گراف بعنوان یک ابزار مفید برای تعیین کمیت و ساده سازی بسیاری از بخش‌های متحرک سیستم‌های پویا در نظر گرفته می‌شود و با توجه به مجموعه‌ای از گره‌ها و اتصالات، می‌توان هر چیزی را از طرح‌بندی شهر گرفته تا داده‌های کامپیوتری، بصورت یک زبان ریاضی معنادار تبدیل کرد. امروزه برنامه‌های کاربردی زیادی برپایه نظریه گراف طراحی و توسعه یافته‌اند.
در نظریه گراف دور اویلری یا مدار اویلری (Eulerian circuit) به مسیری گفته می‌شود که از یک رأس شروع شود و از تمامی یال‌ها یکبار (و فقط یکبار) بگذرد و به همان رأس بازگردد. اگر مسیر از تمام یال‌ها عبور کند ولی به جای اولش بازنگردد به آن مسیر اویلری (Eulerian path) می‌گویند.
معرفی نظریه گراف
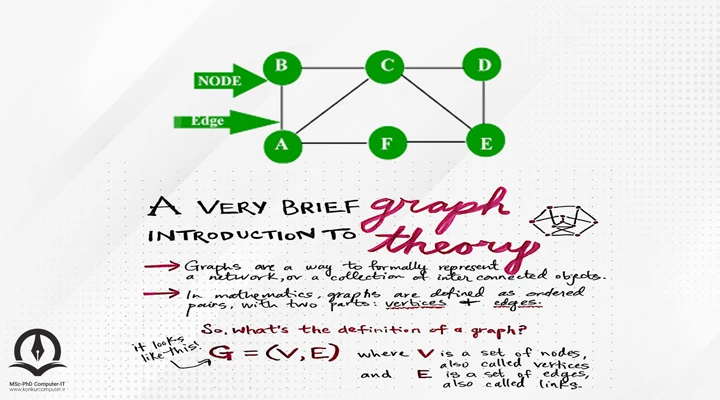
واژه گراف در ترجمه تحت الفظی به معنای نمودار است اما با نمودارهای خطی یا میله‌ای که اغلب ما میشناسیم متفاوت است. گراف‌ها نوعی از داده ساختارهای غیرخطی هستند و یکی از اصلی ترین ویژگی‌های آنها این است که داده‌های آنها از یک ترتیب خاص پیروی نمی‌کنند. در واقع تئوری گراف بعنوان یک شبکه با مجموعه‌ای از نقاط و خطوط شناخته می‌شود که در آن اشیاء یا افراد را می‌توان بعنوان نقاط و ارتباط میان آنها را خطوط شبکه در نظر گرفت.
تعریف گراف به زبان ریاضی عبارتست از: G=(V,E) که V (Vertices or Nodes) مجموعه‌ای ناتهی از رئوس و E (Edge) مجموعه یال‌هاست.
طوقه: اگر از یک رأس به خودش یال وجود داشته باشد، طوقه می‌نامند.
یال چندگانه: اگر بین دو رأس چندین یال وجود داشته باشد، یال چندگانه گویند.
درجه یک رأس: تعداد یال‌های متصل به یک رأس را درجه آن رأس می‌نامیم. به دلایلی، طوقه را دو بار در درجه حساب می‌کنیم. اگر خود راس را با V نمایش دهیم درجه آن را با dV نمایش می‌دهیم. تعداد یال‌های متصل به یک رأس را درجه آن رأس می‌نامیم.
مجاورت:
- در یک گراف دو رأس را مجاور گویند، اگر یک یال بین آنها وجود داشته باشد.
- در یک گراف دو یال را مجاور گویند، اگر یک رأس مشترک بین آنها وجود داشته باشد.
تفاوت گراف با درخت
داده ساختارهای درخت همواره با یک گره به نام ریشه شروع می‌شوند و ممکن است به گره‌های دیگر متصل شوند و این به این معناست که یک درخت می‌تواند شامل چندین زیر درخت در ساختار خود باشد. درختان با مجموعه‌ای از قوانین تعریف می‌شوند؛ یک گره ریشه ممکن است به دیگران متصل باشد یا نباشد، اما در نهایت، همه گره‌ها از یک مکان خاص (ریشه) سرچشمه می‌گیرند. برخی درخت‌ها قوانین خاص‌تری دارند، مانند درخت‌های جستجوی دودویی، که هر گره فقط می‌تواند حداکثر دو پیوند به دو گره (دو فرزند) داشته باشد.
هر درخت فقط می‌تواند در یک جهت جریان داشته باشد، از گره ریشه به گره‌های برگ یا گره‌های فرزند، همچنین یک درخت می‌تواند فقط اتصالات یک طرفه داشته باشد، یعنی یک گره فرزند فقط می‌تواند یک والد داشته باشد؛ درنهایت درخت نمی‌تواند هیچ حلقه یا دوری داشته باشد.
درخت‌ها دارای یک ساختار سلسله مراتبی هستند زیرا می‌توان آنها را در سطوح مختلف بازآرایی کرد که در نهایت منجر به ایجاد یک سلسله مراتب می‌شود.
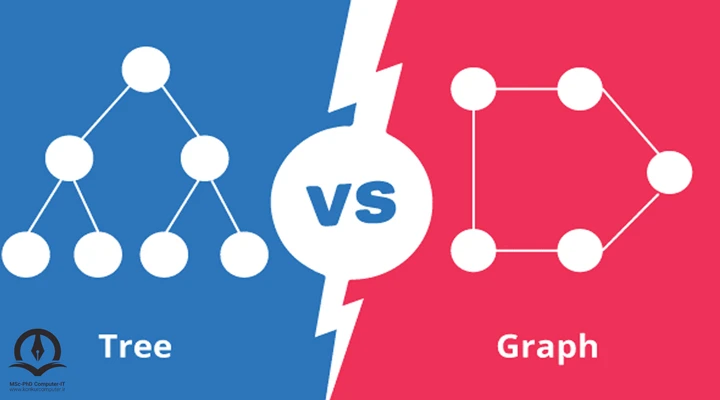
اما گراف‌ها با هیچ کدام از این محدودیت‌ها سازگار نیستند، بعنوان مثال گراف‌ها هیچ مفهومی از گره "ریشه" ندارند و گره‌ها را می‌توان به هر طریق ممکن متصل کرد (یک گره ممکن است به پنج گره دیگر متصل شود!) از طرفی گراف‌ها محدود به جریان "یک جهته" نیستند و در عوض، ممکن است جهت دار بوده و یا هیچ جهتی نداشته باشند. همچنین گراف‌ها می‌توانند دور یا حلقه داشته باشند. این نوع ساختمان دادهآموزش ساختمان داده و الگوریتم
هر ساختمان داده یک نوع فرمت ذخیره‌سازی و مدیریت داده‌ها در کامپیوتر است، که امکان دسترسی و اصلاح کارآمد آن داده‌ها را برای یکسری از الگوریتم‌ها و کاربردها فراهم می‌کند، در این صفحه به بررسی و آموزش ساختمان داده و الگوریتم پرداخته شده است به طور کلی به عنوان یک سیستم شبکه نامیده می‌شود. به عنوان مثال، اینستاگرام یک سایت شبکه اجتماعی است که به طور کلی از ساختار داده‌های گراف استفاده می‌کند.
انواع گراف
همانطور که در بخش قبل گفته شد، هیچ قانون واقعی برای اتصال یک گره به گره دیگر در یک گراف وجود ندارد. یال‌ها (گاهی اوقات به آنها پیوند گفته می‌شود) می‌توانند گره‌ها را به هر طریق ممکن به هم متصل کنند.
گراف‌ها را براساس یال‌ها و جهت و وزن آنها، می‌توان به انواع مختلفی دسته بندی کرد و برای یک برنامه نویسبرنامه نویسی کامپیوتر چیست و چطور می توانید یک برنامه نویس موفق شوید؟
در عصر فعلی برنامه‌نویسی یکی از پرطرفدارترین شغل‌های دنیاست، دغدغه‌‌ای افرادی که می‌خواهند در مسیر برنامه‌نویس شدن قدم بردارند این است که نمی‌دانند از کجا باید شروع کنند، در این صفحه هر آن چه برای تبدیل شدن به یک برنامه نویس حرفه ای نیاز دارید در اختیارتان قرار گرفته است لازم است که در هنگام حل مسائل با ساختار گراف درک صحیح و درستی از نوع گراف به کار رفته در برنامه داشته باشد.
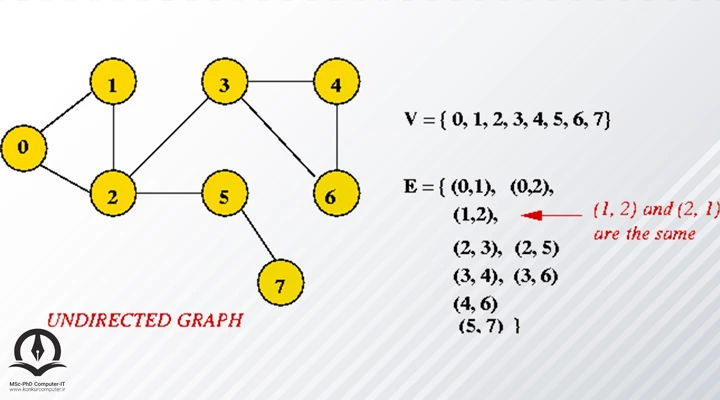
گراف بدون جهت (Undirected Graph)
همانطور که از نام آن مشخص است، هیچ جهتی بین دو نود یا رأس در این نوع از گراف وجود ندارد. بنابراین یال متصل از گره 1 به 2 با یال خروجی از گره 2 به گره 1 یکسان است.
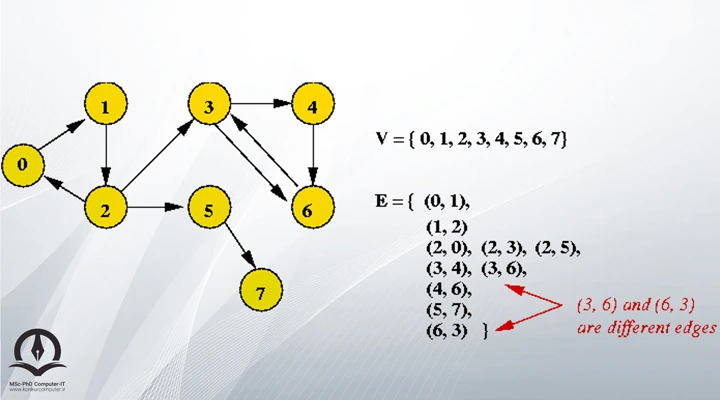
گراف جهت دار (Directed Graphs or DiGraphs)
برخلاف گراف‌های بدون جهت، گراف‌های جهتدار در میان گره‌های مختلف دارای جهت هستند و دو گره به روشی خاص به یکدیگر متصل می‌شوند. بعنوان مثال اگر یک یال از گره 1 به 2 وجود داشته باشد، فقط می توان از 1 به 2 حرکت کرد و کاملاً واضح است، به گره‌ای که از آنجا شروع می‌کنیم به عنوان مبدا و گره‌ای که به آن سفر می‌کنیم به عنوان مقصد اشاره کنیم. در یک یال جهتدار، ما فقط می‌توانیم از مبدا به مقصد سفر کنیم و هرگز برعکس آن امکانپذیر نخواهد بود.
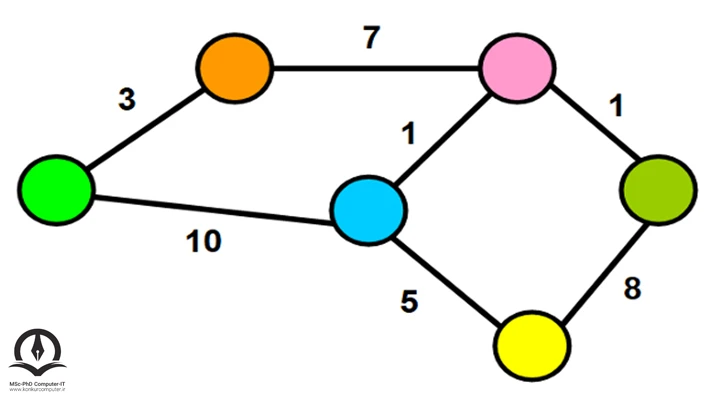
گراف‌های وزن دار می‌توانند جهتدار یا بی‌جهت باشند، بعنوان مثال شکل زیر یک گراف وزن‌دار بی‌جهت است و اعداد روی یال‌ها نشانگر وزن آنها است.
کاربردهای گراف
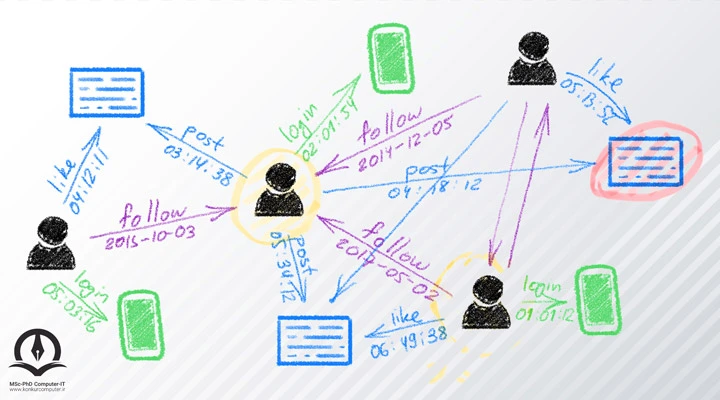
گراف‌ها در اطراف ما هستند اما همیشه آنها را آن طور که هستند نمی‌بینیم. شما در حال حاضر با خواندن این مقاله، به معنای واقعی کلمه روی یک گراف قرار گرفته‌اید. وب یک ساختار گراف عظیم است! وقتی بین وب‌سایت‌ها کلیک می‌کنیم و بین URLها به جلو و عقب حرکت می‌کنیم، در واقع در حال حرکت بر روی یک گراف هستیم. گاهی اوقات این گراف‌ها دارای گره‌هایی با یال‌های غیرجهت‌دار هستند و ما می‌توانیم از یک صفحه وب به صفحه‌ی دیگر به عقب و جلو برویم و گاهی دارای صفحاتی جهتدار هستند که تنها می‌توان از صفحه وب A به صفحه وب B رفت و حرکت برعکس آن ممکن نخواهد بود. اما یک مثال بهتری وجود دارد که تعاملات روزانه ما با گراف‌ها را به زیبایی نشان می‌دهد: شبکه‌های اجتماعی.
فیس‌بوک بعنوان یک شبکه اجتماعی عظیم، نوعی گراف است. و اگر بیشتر در مورد عملکرد واقعی آن فکر کنیم، بهتر متوجه می‌شویم که دقیقاً چه نوع گرافی است. در فیس‌بوک، اگر شخصی شما را به عنوان دوست اضافه کند، باید درخواست او را بپذیرید و امکان ندارد که این تعامل بصورت یک طرفه صورت پذیرد. بنابراین رابطه بین دو کاربر (گره‌ها یا رئوس در قالب گراف!) دو طرفه است و هیچ مفهومی از گره "مبدا" و "مقصد" وجود ندارد.
آیا می توانید حدس بزنید که فیس‌بوک با چه نوع نموداری پیاده سازی شده است؟ بله کاملاً درست است ، گراف بدون جهت!
از طرف دیگر توییتر با فیس‌بوک بسیار متفاوت عمل می‌کند. شما می‌توانید فردی را دنبال کنید، اما او ممکن است شما را دنبال نکند. بعنوان مثال، شما ممکن است یک بازیگر یا سیاستمدار و یا هر فرد معروف دیگری را دنبال کنید، اما او قطعاً شما را دنبال نمی‌کند (متاسفانه!). بنابراین ما می‌توانیم توییتر را به‌عنوان یک گراف جهتدار نمایش دهیم. هر یالی که ایجاد می‌کنیم نشان دهنده یک رابطه یک طرفه است. وقتی فردی را در توییتر دنبال می‌کنید، یک یال در گراف با حساب خود به عنوان گره مبدا و حساب فرد مقابل به عنوان گره مقصد ایجاد می‌کنید.
الگوریتم های معروف گراف
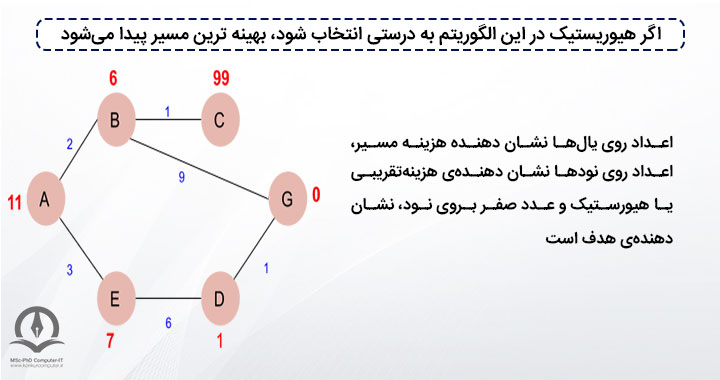
الگوریتم A* (A-Star)
*A یک الگوریتم جستجوی آگاهانه (Informed Search) یا بهترین جستجوی اول است که بر اساس گراف‌های وزنی طراحی شده و با شروع از یک گره خاص و حرکت به سمت گره هدف معین، کوتاه‌ترین مسیر طی شده در کمترین زمان را در گراف می‌یابد. این الگوریتم از یک مفهوم به نام تابع اکتشافی (Heuristic Function) برای یافتن یک هدف خاص با کوتاه‌ترین مسیر بهره می‌برد. در هر تکرار از حلقه اصلی خود، *A باید تعیین کند که کدام یک از مسیرهای خود را گسترش دهد و این کار را بر اساس هزینه مسیر و برآورد یا تخمین هزینه مورد نیاز (هیورستیک) برای رسیدن به هدف انجام می‌دهد. به طور خاص،*A مسیری را انتخاب می‌کند که حداقل باشد. الگوریتم *A بااینکه یکی از بهترین الگوریتم‌های مسیریابی است اما همیشه کوتاه‌ترین مسیر را ایجاد نمی‌کند، زیرا به شدت به تابع اکتشافی وابسته است.
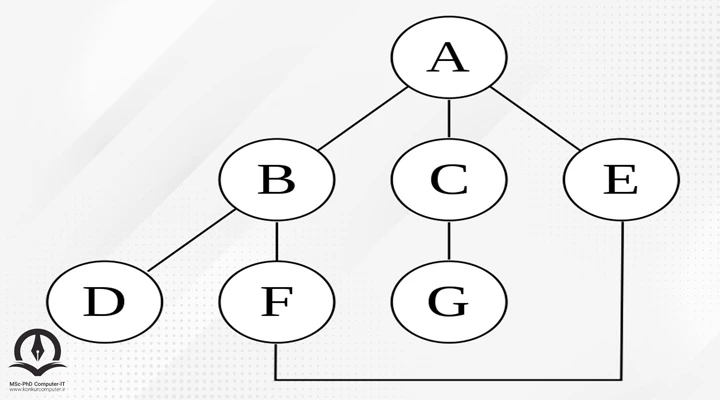
الگوریتم جستجوی عمق اول (DFS: Depth First Search)
الگوریتم جستجوی عمق اول برای پیمایش یا جستجو در ساختارهای داده درختی یا گرافی است. همانطور که در فصل گراف درس طراحی الگوریتمآموزش طراحی الگوریتم به زبان ساده
درس طراحی الگوریتم یکی از مهم‌ترین و بنیادیترین دروس رشته کامپیوتر است. هدف از این درس، معرفی روش‌های مختلف طراحی الگوریتم‌ها برای حل مسائل گوناگون است، در این صفحه به معرفی و آموزش طراحی الگوریتم پرداخته شده است. می‌خوانیم، این الگوریتم از گره ریشه شروع می‌شود (انتخاب گره دلخواه به عنوان گره ریشه در مورد یک گراف) و تا آنجا که ممکن است در امتداد هر شاخه قبل از عقب‌نشینی کاوش می‌کند. یک جستجوی عمقی که از گره A شروع می‌شود، با فرض اینکه یال‌های چپ در نمودار نشان داده شده، قبل از یال‌های راست انتخاب شده‌اند و الگوریتم جستجو، گره‌های بازدید شده قبلی را به خاطر می‌آورد و آنها را تکرار نمی‌کند، بازدید خواهد شد. گره‌ها به ترتیب زیر هستند: A,B,D,F,E,C,G. انجام همان جستجو بدون به‌خاطر سپردن گره‌های بازدید شده قبلی منجر به بازدید از گره‌ها به ترتیب ...,A,B,D,F,E,A,B,D,F,E برای همیشه می‌شود که در A,B,D، گرفتار می‌شوند. چرخه F وE هرگز به C یا G نمی‌رسد. یکی از مزیت‌های جستجوی عمق اول در ساختار گراف، اجتناب از حلقه بی‌نهایت است و به همه گره‌ها می‌رسد.
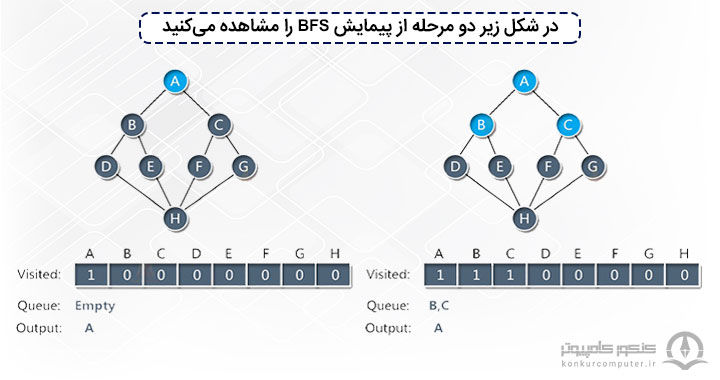
الگوریتم جستجوی سطح اول (BFS: Breadth-first search)
الگوریتم جستجوی سطح اول، از جمله الگوریتم‌های مشهور پیمایش و جستجوی گراف است که در حل مسائل الگوریتمی و هوش مصنوعیهوش مصنوعی (AI) چیست؟ انواع، کاربردها، مزایا و معایب
هوش مصنوعی یا Artificial Intelligence یا به اختصار AI، امروزه کاربردهای بسیاری پیدا کرده و به یکی از داغ‌ترین حوزه‌های بشر تبدیل شده است، اما با این وجود بسیاری از افراد با کاربردهای آن آشنایی کامل ندارند، به همین علت در این صفحه کاربردها، مزایا و معایب AI بطور کامل بررسی شده است کاربرد دارد. در یک گراف، پیمایش می‌تواند از هر گره‌ای شروع شود و تمام گره‌ها را از نظر سطح پوشش دهد. الگوریتم BFS از ساختار داده صف برای پیاده‌سازی استفاده می‌کند. در BFS، ما همیشه به حالت هدف نهایی می‌رسیم در حالی‌که همیشه برای الگوریتم DFS صدق نمی‌کند. الگوریتم BFS با وارد کردن گره مبدأ به صف پردازش شروع شده و تا خالی نشدن این صف مراحل زیر را تکرار می‌کند:
- عنصر جلوی صف را به عنوان گره جاری انتخاب و از صف حذف می‌کند.
- گره جاری را پردازش می‌کند.
- گره‌های مجاور گره جاری که پردازش نشده و در صف پردازش نیز قرار ندارند را به این صف اضافه می‌کند.
جمع‌بندی
در پایان، امیدواریم شما را متقاعد کرده باشیم که نظریه گراف فقط یک مفهوم انتزاعی ریاضی نیست، بلکه در واقعیت کاربردهای مفید و جالب بسیاری دارد! همچنین دل‌خوشیم براینکه مطالب بالا برای برخی از شما در حل مسائل مشابه مفید واقع شده باشد و یا حداقل در مورد نظریه گراف و برخی از کاربردهای آن کمی کنجکاوی شما را برآورده کند. در آخر نیز باید به این نکته اشاره کنیم که درس نظریه گراف بعنوان یکی از دروس مهم در رشته‌های علوم کامپیوتر و علوم ریاضی است و در زمینه‌های مختلفی در علم کامپیوتر مانند مسیریابی در شبکه، بهینه سازی و رمز گذاری کاربرد دارد.
کیان انواری 
علیرضا بهدوست 
احسان داستانی 
معین منعمی 
علیرضا حسن زاده باقی 
سعيد نوروزيان 
بهمن قائدی 
مهدی مزارعی 
سینا مهرآبادی 
محمد امین شنابی 
سارا مختاری همامی 
Amir hossein 
emelkabi 
محمد چاروسایی 
علیرضا ملکی 
علی فتحی وافق 
غزل موسوی 
مرتضی آشوری 
انوش مه جبین 
سعید راصدی 
یوسف عباسی 
مهدی حسنی 
احمد بنائیان 
فاطمه سادات لطفی فاطمی 
محمد رضا کمالی 
حسین پری نور 
پریسا نکوگل 
محسن سروری 
فاطمه اکبرنژاد 
علی بابایی 
مجید محمددوست 
هانیه طالبی 
اسما سهرابی 
الینا اشرف پور 
