کنکور کامپیوتر
0
ورود | ثبت نام
کنکور کامپیوترالگوریتم جانسون⚡️توضیح و آموزش الگوریتم جانسون
نظرات
اشتراک
بالا
علاقه‌مندی

اشتراک
 
راهنمای انتخاب موضوع
الگوریتم جانسون⚡️توضیح و آموزش الگوریتم جانسون
کنکور کامپیوترالگوریتم جانسون⚡️توضیح و آموزش الگوریتم جانسون

الگوریتم جانسون⚡️توضیح و آموزش الگوریتم جانسون

این مقاله عالی به معرفی الگوریتم جانسون (Johnson's algorithm) پرداخته همچنین توضیح الگوریتم جانسون، آموزش الگوریتم جانسون و مثال الگوریتم جانسون را آورده

الگوریتم جانسون راهی برای یافتن کوتاه‌ترین مسیرها بین تمام جفت‌ رئوس‌ها در یک گراف جهت دار با یال‌های وزن دار است. این اجازه می‌دهد تا برخی از وزن‌های یال‌ها اعداد منفی باشند اما هیچ دور منفی نباید وجود نداشته باشد. این الگوریتم با استفاده از الگوریتم بلمن-فورد برای محاسبه تبدیل گراف ورودی که تمام وزن‌های منفی را حذف می‌کند، کار می‌کند و به الگوریتم دایکسترا اجازه می‌دهد در گراف تبدیل‌شده استفاده شود. در این مقاله با این الگوریتمالگوریتم چیست به زبان ساده و با مثال های فراوانالگوریتم چیست به زبان ساده و با مثال های فراواندر این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد آشنا خواهید شد و نحوه پیاده‌سازی آن را با زبان‌های برنامه نویسی پایتونزبان برنامه نویسی پایتون چیست؟ – نحوه شروع و دلایل محبوبیتزبان برنامه نویسی پایتون چیست؟ – نحوه شروع و دلایل محبوبیتزبان برنامه نویسی پایتون (Python) چیست؟ این مقاله عالی به بررسی دلایل محبوبیت پایتون، موارد استفاده از پایتون و نحوه شروع به برنامه نویسی پایتون پرداخته، جاوا اسکریپتجاوا اسکریپت چیست؟ معرفی زبان برنامه نویسی java scriptجاوا اسکریپت چیست؟ معرفی زبان برنامه نویسی java scriptزبان برنامه نویسی جاوا اسکریپت چیست و چه کاربردی دارد؟ این صفحه عالی به بررسی مزایای JavaScript پرداخته و مبانی برنامه نویسی جاوا اسکریپت را آموزش داده و سی پلاس پلاسبرنامه نویسی سی پلاس پلاس چیست؟ مزایای برنامه نویسی C++‎؟برنامه نویسی سی پلاس پلاس چیست؟ مزایای برنامه نویسی C++‎؟برنامه نویسی سی پلاس پلاس چیست و چه کاربردی دارد؟ این صفحه عالی به بررسی مزایای برنامه نویسی C++ پرداخته و نمونه هایی از کدهای زبان برنامه نویسی ++C را آورده خواهید دید.

الگوریتم جانسون

الگوریتم جانسون

الگوریتم جانسون بر روی گراف‌های جهت دار و وزن دار کار می‌کند، به یال‌ها اجازه می‌دهد وزن‌های منفی داشته باشند اما دور منفی نمی‌تواند وجود داشته باشد زیرا در این صورت هیچ کوتاه‌ترین مسیری برای رئوس قابل دستیابی توسط آن دور وجود نخواهد داشت.

الگوریتم جانسون دارای چهار مرحله اصلی است:

در ادامه با یک مثال نحوه کارکرد الگوریتم جانسون را بررسی می‌کنیم.

حتما بخوانید :
معرفی انواع الگوریتم‌ ها

مثال الگوریتم جانسون

گراف زیر را در نظر بگیرید:

مثالی از الگوریتم جانسون

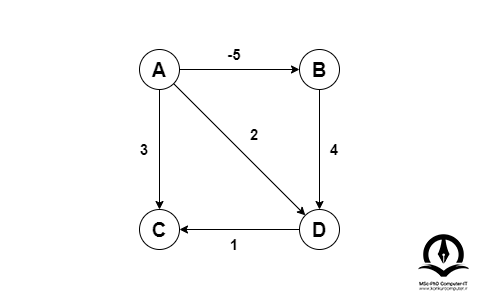
راس S را اضافه می‌کنیم و یال‌هایی را از S به تمام رئوس گراف اصلی اضافه می‌کنیم:

مثالی از الگوریتم جانسون

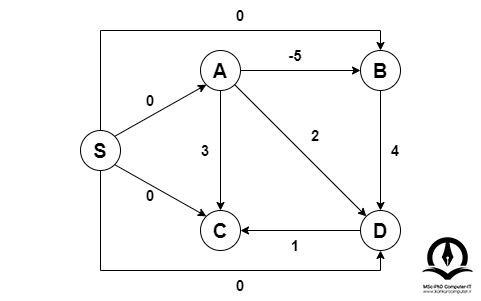
ما با استفاده از الگوریتم بلمن-فورد، کوتاه‌ترین فاصله‌ها را از راس S تا تمام رئوس دیگر محاسبه می‌کنیم. کوتاه‌ترین فاصله از S تا رئوس A ،B ،C و D به ترتیب 0، 5-، 1- و 0 است، یعنی h[ ]={0, -5, -1, 0}. هنگامی که این فاصله‌ها را به دست آوردیم، راس S را حذف کرده و با استفاده از فرمول زیر یال‌ها را دوباره وزن می‌کنیم:

w(u, v) = w(u, v) + h[u] – h[v]

نتیجه نهایی گراف با وزن‌های زیر خواهد بود:

مثالی از الگوریتم جانسون

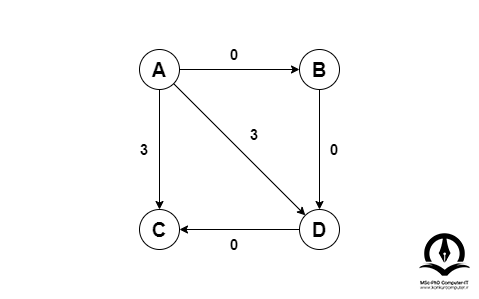
از آنجایی که اکنون همه وزن‌ها مثبت هستند، می‌توانیم الگوریتم دایجستراالگوریتم دایجسترا (Dijkstra) از 0 تا 100 - الگوریتم دایکستراالگوریتم دایجسترا (Dijkstra) از 0 تا 100 - الگوریتم دایکسترااین صفحه الگوریتم دایجسترا (Dijkstra) (یا همان الگوریتم دایکسترا) را از 0 تا 100 بررسی کرده، همین طور به پیاده سازی و آموزش الگوریتم دایجسترا پرداخته است. را برای هر رأس به عنوان راس مبدا اجرا کنیم.

حتما بخوانید :
الگوریتم pso⚡️مزایا و معایب+گام ها و نحوه کار+ پیاده سازی

پیاده‌سازی الگوریتم جانسون

حال که با الگوریتم جانسون آشنا شدیم در ادامه ابتدا به بررسی شبه کد این الگوریتم و سپس به پیاده‌سازی این الگوریتم در زبان های برنامه نویسیزبان های برنامه نویسی چیست؟زبان های برنامه نویسی چیست؟این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده مختلف می‌پردازیم.

شبه کد الگوریتم جانسون

شبه کد زیر، الگوریتم جانسون را در سطح بالایی توصیف می‌کند. زیرروال‌ها توضیح داده نشده‌اند زیرا این الگوریتم‌ها در صفحه بلمن-فورد و صفحه Dijkstra هستند. برای کمک به شما در ارتباط دادن شبه کد به توضیحات الگوریتم، هر یک از مراحل برچسب‌گذاری شده است.

Johnson(G)
    1.
    create G` where G`.V = G.V + {s},
        G`.E = G.E + ((s, u) for u in G.V), and 
        weight(s, u) = 0 for u in G.V
    2.
    if Bellman-Ford(s) == False
        return "The input graph has a negative weight cycle"
    else:
        for vertex v in G`.V:
            h(v) = distance(s, v) computed by Bellman-Ford
        for edge (u, v) in G`.E:
            weight`(u, v) = weight(u, v) + h(u) - h(v)
    3.
        D = new matrix of distances initialized to infinity
        for vertex u in G.V:
            run  (G, weight`, u) to compute distance`(u, v) for all v in G.V
            for each vertex v in G.V:
                D_(u, v) = distance`(u, v) + h(v) - h(u)
        return D

Python

# Implementation of Johnson's algorithm in Python3
 
# Import function to initialize the dictionary
from collections import defaultdict
MAX_INT = float('Inf')
 
# Returns the vertex with minimum
# distance from the source
def minDistance(dist, visited):
 
    (minimum, minVertex) = (MAX_INT, 0)
    for vertex in range(len(dist)):
        if minimum > dist[vertex] and visited[vertex] == False:
            (minimum, minVertex) = (dist[vertex], vertex)
 
    return minVertex
 
 
# Dijkstra Algorithm for Modified
# Graph (removing negative weights)
def Dijkstra (graph, modifiedGraph, src):
 
    # Number of vertices in the graph
    num_vertices = len(graph)
 
    # Dictionary to check if given vertex is
    # already included in the shortest path tree
    sptSet = defaultdict(lambda : False)
 
    # Shortest distance of all vertices from the source
    dist = [MAX_INT] * num_vertices
 
    dist[src] = 0
 
    for count in range(num_vertices):
 
        # The current vertex which is at min Distance
        # from the source and not yet included in the
        # shortest path tree
        curVertex = minDistance(dist, sptSet)
        sptSet[curVertex] = True
 
        for vertex in range(num_vertices):
            if ((sptSet[vertex] == False) and
                (dist[vertex] > (dist[curVertex] +
                modifiedGraph[curVertex][vertex])) and
                (graph[curVertex][vertex] != 0)):
                 
                dist[vertex] = (dist[curVertex] +
                                modifiedGraph[curVertex][vertex]);
 
    # Print the Shortest distance from the source
    for vertex in range(num_vertices):
        print ('Vertex ' + str(vertex) + ': ' + str(dist[vertex]))
 
# Function to calculate shortest distances from source
# to all other vertices using Bellman-Ford algorithm
def BellmanFord(edges, graph, num_vertices):
 
    # Add a source s and calculate its min
    # distance from every other node
    dist = [MAX_INT] * (num_vertices + 1)
    dist[num_vertices] = 0
 
    for i in range(num_vertices):
        edges.append([num_vertices, i, 0])
 
    for i in range(num_vertices):
        for (src, des, weight) in edges:
            if((dist[src] != MAX_INT) and
                    (dist[src] + weight < dist[des])):
                dist[des] = dist[src] + weight
 
    # Don't send the value for the source added
    return dist[0:num_vertices]
 
# Function to implement Johnson Algorithm
def JohnsonAlgorithm(graph):
 
    edges = []
 
    # Create a list of edges for Bellman-Ford Algorithm
    for i in range(len(graph)):
        for j in range(len(graph[i])):
 
            if graph[i][j] != 0:
                edges.append([i, j, graph[i][j]])
 
    # Weights used to modify the original weights
    modifyWeights = BellmanFord(edges, graph, len(graph))
 
    modifiedGraph = [[0 for x in range(len(graph))] for y in
                    range(len(graph))]
 
    # Modify the weights to get rid of negative weights
    for i in range(len(graph)):
        for j in range(len(graph[i])):
 
            if graph[i][j] != 0:
                modifiedGraph[i][j] = (graph[i][j] +
                        modifyWeights[i] - modifyWeights[j]);
 
    print ('Modified Graph: ' + str(modifiedGraph))
 
    # Run Dijkstra for every vertex as source one by one
    for src in range(len(graph)):
        print ('\nShortest Distance with vertex ' +
                        str(src) + ' as the source:\n')
        Dijkstra(graph, modifiedGraph, src)
 
# Driver Code
graph = [[0, -5, 2, 3],
        [0, 0, 4, 0],
        [0, 0, 0, 1],
        [0, 0, 0, 0]]
 
JohnsonAlgorithm(graph)

C++

#include<iostream>
#define INF 9999
using namespace std;
int min(int a, int b);
int cost[10][10], adj[10][10];
inline int min(int a, int b){
   return (a<b)?a:b;
}
main() {
   int vert, edge, i, j, k, c;
   cout < "Enter no of vertices: ";
   cin > vert;
   cout < "Enter no of edges: ";
   cin > edge;
   cout < "Enter the EDGE Costs:\n";
   for (k = 1; k ≤ edge; k++) { //take the input and store it into adj and cost matrix
      cin > i > j > c;
      adj[i][j] = cost[i][j] = c;
   }
   for (i = 1; i ≤ vert; i++)
      for (j = 1; j ≤ vert; j++) {
         if (adj[i][j] == 0 && i != j)
            adj[i][j] = INF; //if there is no edge, put infinity
      }
   for (k = 1; k ≤ vert; k++)
      for (i = 1; i ≤ vert; i++)
         for (j = 1; j ≤ vert; j++)
            adj[i][j] = min(adj[i][j], adj[i][k] + adj[k][j]); //find minimum path from i to j through k
   cout << "Resultant adj matrix\n";
   for (i = 1; i ≤ vert; i++) {
      for (j = 1; j ≤ vert; j++) {
            if (adj[i][j] != INF)
               cout < adj[i][j] < " ";
      }
      cout << "\n";
   }
}

JavaScript

// Initialize the dictionary
const MAX_INT = Number.POSITIVE_INFINITY;
 
// Returns the vertex with minimum distance from the source
function minDistance(dist, visited) {
  let minimum = MAX_INT;
  let minVertex = 0;
  for (let vertex = 0; vertex < dist.length; vertex++) {
    if (minimum > dist[vertex] && !visited[vertex]) {
      minimum = dist[vertex];
      minVertex = vertex;
    }
  }
  return minVertex;
}
 
// Dijkstra Algorithm for Modified Graph (removing negative weights)
function Dijkstra(graph, modifiedGraph, src) {
  const numVertices = graph.length;
 
  // Dictionary to check if given vertex
  // is already included in the shortest path tree
  const sptSet = new Array(numVertices).fill(false);
 
  // Shortest distance of all vertices from the source
  const dist = new Array(numVertices).fill(MAX_INT);
  dist[src] = 0;
 
  for (let count = 0; count < numVertices; count++) {
    // The current vertex which is at min Distance
    // from the source and not yet included in the shortest path tree
    const curVertex = minDistance(dist, sptSet);
    sptSet[curVertex] = true;
 
    for (let vertex = 0; vertex < numVertices; vertex++) {
      if (
        !sptSet[vertex] &&
        dist[vertex] > dist[curVertex] + modifiedGraph[curVertex][vertex] &&
        graph[curVertex][vertex] !== 0
      ) {
        dist[vertex] = dist[curVertex] + modifiedGraph[curVertex][vertex];
      }
    }
  }
 
  // Print the Shortest distance from the source
  for (let vertex = 0; vertex < numVertices; vertex++) {
    console.log(`Vertex ${vertex}: ${dist[vertex]}`);
  }
}
 
// Function to calculate shortest distances from source to all other vertices using Bellman-Ford algorithm
function BellmanFord(edges, graph, numVertices) {
  // Add a source s and calculate its min distance from every other node
  const dist = new Array(numVertices + 1).fill(MAX_INT);
  dist[numVertices] = 0;
 
  for (let i = 0; i < numVertices; i++) {
    edges.push([numVertices, i, 0]);
  }
 
  for (let i = 0; i < numVertices; i++) {
    for (const [src, des, weight] of edges) {
      if (dist[src] !== MAX_INT && dist[src] + weight < dist[des]) {
        dist[des] = dist[src] + weight;
      }
    }
  }
 
  // Don't send the value for the source added
  return dist.slice(0, numVertices);
}
 
// Function to implement Johnson Algorithm
function JohnsonAlgorithm(graph) {
  const edges = [];
 
  // Create a list of edges for Bellman-Ford Algorithm
for (let i = 0; i < graph.length; i++) {
for (let j = 0; j < graph[i].length; j++) {
if (graph[i][j] !== 0) {
edges.push([i, j, graph[i][j]]);
}
}
}
 
// Weights used to modify the original weights
const modifyWeights = BellmanFord(edges, graph, graph.length);
 
const modifiedGraph = Array(graph.length).fill().map(() => Array(graph.length).fill(0));
 
// Modify the weights to get rid of negative weights
for (let i = 0; i < graph.length; i++) {
for (let j = 0; j < graph[i].length; j++) {
if (graph[i][j] !== 0) {
modifiedGraph[i][j] = graph[i][j] + modifyWeights[i] - modifyWeights[j];
}
}
}
 
console.log("Modified Graph: " + JSON.stringify(modifiedGraph)+"<br />");
 
// Run Dijkstra for every vertex as source one by one
for (let src = 0; src < graph.length; src++) {
console.log("
"+ "Shortest Distance with vertex " + src + " as the source:"+"
");
Dijkstra(graph, modifiedGraph, src);
}
}
 
// Driver Code
const graph = [[0, -5, 2, 3],
[0, 0, 4, 0],
[0, 0, 0, 1],
[0, 0, 0, 0]
];
 
JohnsonAlgorithm(graph);

پیچیدگی زمانی الگوریتم جانسون

مراحل اصلی در الگوریتم جانسون عبارتند از الگوریتم بلمن-فورد که یک بار و دایکسترا که V بار فراخوانی می‌شود. پیچیدگی زمانی بلمن فورد O(VE) و پیچیدگی زمانی دایکسترا O(VLogV) است بنابراین پیچیدگی زمانی کلی الگوریتم جانسون O(V2log V + VE) است.

حتما بخوانید :
الگوریتم پریم (Prim) چیست ⚡️مثال+پیاده سازی+پیچیدگی زمانی

کاربردهای الگوریتم جانسون

کاربردهای مختلفی برای الگوریتم جانسون وجود دارد که برخی از آنها به شرح زیر است:

جمع‌بندی

در این مقاله با الگوریتم جانسون آشنا شدیم. ما همچنین در مورد عملکرد الگوریتم جانسون آموختیم و دیدیم که چگونه الگوریتم جانسون از الگوریتم دایکسترا و الگوریتم بلمن فورد برای افزایش کارایی الگوریتم جانسون استفاده می‌کند، همینطور یاد گرفتیم که چگونه الگوریتم جانسون را پیاده‌سازی کنیم؛ همچنین پیچیدگی زمانی این الگوریتم را تحلیل کردیم و با کاربردهای آن در دنیای واقعی آشنا شدیم.

الگوریتم جانسون چیست؟

الگوریتم جانسون راهی برای یافتن کوتاه‌ترین مسیرها بین تمام جفت‌های رئوس در یک گراف جهت‌دار با یال‌های وزن‌دار است. این الگوریتم اجازه می‌دهد تا برخی از وزن‌های یال‌ها اعداد منفی باشند، اما هیچ دور منفی نباید در گراف وجود نداشته باشد.

پیچیدگی زمانی الگوریتم جانسون از چه مرتبه‌ای است؟

پیچیدگی زمانی این الگوریتم از مرتبه O(V2log V + VE) است.

در الگوریتم جانسون از چه الگوریتم‌های دیگری استفاده می‌شود؟

در الگوریتم جانسون از الگوریتم بلمن-فورد و الگوریتم دایکسترا استفاده می‌شود.

امتیازدهی5 1 1 1 1 1 1 1 1 1 15.00 امتیاز (2 رای)
اشتراک
برچسب‌ها :
13
12
5
16
19
14
11
22
17

مطالب مرتبط

همه مقالات
طراحی الگوریتم چیست؟ آموزش طراحی الگوریتم به زبان ساده

طراحی الگوریتم چیست؟ آموزش طراحی الگوریتم به زبان ساده

اصطلاحات ساختمان داده به انگلیسی

اصطلاحات ساختمان داده به انگلیسی

یادگیری ماشین با پایتون⚡️نقشه راه یادگیری ماشین با پایتون

یادگیری ماشین با پایتون⚡️نقشه راه یادگیری ماشین با پایتون

بهترین زبان برنامه نویسی برای شروع‌ چیست؟

بهترین زبان برنامه نویسی برای شروع‌ چیست؟

معرفی ارشد شبکه های کامپیوتری دانشگاه صنعتی شریف

معرفی ارشد شبکه های کامپیوتری دانشگاه صنعتی شریف

معرفی بهترین دانشگاه های ایران در رشته فناوری اطلاعات

معرفی بهترین دانشگاه های ایران در رشته فناوری اطلاعات

صحبت با هوش مصنوعی گوگل

صحبت با هوش مصنوعی گوگل

معرفی گرایش رایانش امن مقطع ارشد دانشگاه شریف

معرفی گرایش رایانش امن مقطع ارشد دانشگاه شریف

ظرفیت مهندسی کامپیوتر شریف

ظرفیت مهندسی کامپیوتر شریف

مشاهده تمامی مقالات
رتبه بندی دانشگاه های ایران + معرفی بهترین دانشگاه های ایران

رتبه بندی دانشگاه های ایران + معرفی بهترین دانشگاه های ایران

منابع کنکور ارشد کامپیوتر

منابع کنکور ارشد کامپیوتر

معرفی رشته آی تی (رشته فناوری اطلاعات)

معرفی رشته آی تی (رشته فناوری اطلاعات)

گرایش های ارشد کامپیوتر

گرایش های ارشد کامپیوتر

رشته کامپیوتر فنی حرفه ای و ادامه تحصیل این رشته در دانشگاه

رشته کامپیوتر فنی حرفه ای و ادامه تحصیل این رشته در دانشگاه

مشاهده تمامی مقالات
14
11
22
17
13
12
5
16
19
بارگذاری نظرات
تلگرام اینستاگرام