ویدیو حل تشریحی رایگان سیگنال و سیستمها کنکور ارشد کامپیوتر 1403
آسان یک سیستم پیوسته با رابطۀ $y\left(t\right)\left(x^2\left(t\right)-1\right)=2$ و یک سیستم گسسته با رابطه $y\left[n\right]=\left(n+1\right)2^{x\left[n\right]}$ توصیف شده‌اند. در مورد این دو سیستم، کدام گزاره درست است؟ سیستمها
راه حل اول:
ابتدا به بررسی خطی بودن دو سیستم میپردازیم، در سیستم پیوسته چون خروجی برحسب ورودی از درجه 2 است، پس خطی نیست همچنین در سیستم گسسته خروجی بر حسب ورودی نمایی است چون x در توان است پس نمیتواند خطی باشد (رد گزینه 2) در مورد وارون پذیری شرط وارون پذیر بودن این است که ورودی در همه لحظات از روی خروجی قابل بازیابی باشد در سیستم گسسته در لحظه n=-1 حاصل خروجی برابر صفر گردیده ومشخص نیست به ازای چه ورودی خروجی صفر شده لذا نمیتوان ورودی را از از خروجی بدست اورد پس وارون پذیر نیست .
در مورد تغییر ناپذیری با زمان هم باید با شیفت زمانی ورودی به اندازه مثلا t0 خروجی به همین میزان تغییر کند که به وضوح در سیستم گسسته عبارت (n+1) این موضوع را نقض میکند و سیستم تغییر ناپذیر با زمان نیست لذا گزینه 1 صحیح است برای چک کردن علی بودن هم باید توجه کنید که خروجی در هر لحظه به ورودی در آینده بستگی نداشته باشد با توجه به این که هر دو سیستم بی حافظه هستند یعنی خروجی در هر لحظه به ورودی در همان لحظه بستگی دارد پس قطعا علی هم هستند و گزینه 1 صحیح است.
راه حل دوم:
گزینه 1 درست است.
بررسی گزینه 1): سیستم عِلّی، سیستمی است که خروجی آن در لحظه $t_0$، به مقادیر ورودی لحظات بعد از $t_0$ بستگی نداشته باشد.
در سیستم پیوسته $y\left(t\right)=\frac{2}{x^2\left(t\right)-1}$ : خروجی در لحظه‌ی $t_0$ به مقادیر ورودی در لحظه $t_0$ وابسته است.
در سیستم گسسته $y\left[n\right]=\left(n+1\right)2^{x\left[n\right]}$ : خروجی در لحظه‌ی $n_0$ به مقادیر ورودی در لحظه‌ی $n_0$ وابسته است؛ درنتیجه هردو سیستم عِلّی هستند. این گزینه درست است.
بررسی گزینه 2): سیستمی خطی است که رابطه‌ی خروجی آن با ورودی به‌صورت خطی باشد؛ یعنی هم دارای خاصیت همگنی و هم خاصیت جمع‌پذیری باشد. یعنی باید دارای خاصیت زیر باشد:
$T\left\{\alpha x_1\left(t\right)+\beta x_2\left(t\right)\right\}=\alpha T\left\{x_1\left(t\right)\right\}+\beta T\left\{x_2\left(t\right)\right\}$
در حالت کلی هر عملگر غیرخطی که روی ورودی یا خروجی اثر کند سیستم را غیرخطی میکند که در این سؤال ورودی سیستم پیوسته در مخرج است و در سیستم گسسته ورودی در توان ظاهر شده است که درنتیجه هردو سیستم غیرخطی می‌باشند. امّا میتوان خاصیت‌های خطی بودن را نیز بررسی کرد.
در سیستم پیوسته:
$\genfrac{}{}{0pt}{}{T\left\{x\left(t\right)\right\}=\frac{2}{x^2\left(t\right)-1}\ \ \ \ \ \ \ }{T\left\{\alpha x\left(t\right)\right\}=\frac{2}{{\alpha }^2x^2\left(t\right)-1}} \begin{array}{c} \Rightarrow T\left\{\alpha x\left(t\right)\right\}\neq \alpha T\left\{x\left(t\right)\right\} \end{array}$
در سیستم گسسته:
$\genfrac{}{}{0pt}{}{T\left\{x\left[n\right]\right\}=\left(n+1\right)2^{x\left[n\right]}\ \ \ \ }{T\left\{\alpha x\left[n\right]\right\}=\left(n+1\right)2^{\alpha x\left[n\right]}} \begin{array}{c} \Rightarrow \alpha T\left\{x\left[n\right]\right\}\neq T\left\{\alpha x\left[n\right]\right\} \end{array}$
درنتیجه خاصیت خطی برای هیچکدام برقرار نیست و این گزینه صحیح نیست.
بررسی گزینه 3): به سیستمی که به‌ازای ورودی‌های متمایز، خروجی‌های متمایزی دهد سیستم وارون‌پذیر گفته می‌شود. به‌عبارت دیگر در سیستم وارون‌پذیر میتوان ورودی را از روی خروجی بازیابی کرد. زیرا هرخروجی متمایز با یک ورودی است.
در سیستم پیوسته: اگر بخواهیم وارون‌پذیری سیستمی را بدون مثال نقض بررسی کنیم باید تحقیق کنیم که آیا باتوجه به رابطه‌ی سیستم میتوان $x(t)$ را برحسب خروجی به‌صورت یکتا و بدون ابهام نوشت یا خیر.
$y\left(t\right)\left(x^2\left(t\right)-1\right)=2\to x^2\left(t\right)-1=\frac{2}{y\left(t\right)}\to x^2\left(t\right)=\frac{2}{y\left(t\right)}+1 $
$ \to x\left(t\right)=\pm \sqrt{\frac{2}{y\left(t\right)}+1}+\sqrt{\frac{2}{y\left(t\right)}+1}$
ملاحظه می‌کنید به‌ازای هر $y(t)$، دو مقدار $-\sqrt{\frac{2}{y\left(t\right)}+1}$ ،$+\sqrt{\frac{2}{y\left(t\right)}+1}$ برای $x(t)$ به‌دست می‌آید. بنابراین نمیتوان $x(t)$ را از روی $y(t)$ بازیابی نمود.
در سیستم گسسته: شرط لازم برای وارون‌پذیری یک سیستم این است که ورودی همه زمانی همچنین همه مقادیر ورودی، به خروجی منتقل شوند؛ به‌عبارت دیگر خروجی به ورودی همه زمانی و به همه مقادیر ورودی وابسته باشد. اگر چنین نباشد انگار سیستم بعضی‌از مقادیر ورودی را حذف کرده است؛ درنتیجه سیستم وارون‌پذیر نخواهد بود. در سیستم گسسته داریم:
$y\left[n\right]=\left(n+1\right)2^{x\left[n\right]}$
به‌ازای $n=-1$ داریم:
$y\left[-1\right]=0\times 2^{x\left[-1\right]}=0$
درنتیجه $x[-1]$ در خروجی نقشی ندارد؛ درنتیجه سیستم وارون‌پذیر نیست.
هیچکدام از سیستمها وارون‌پذیر نیست، درنتیجه این گزینه صحیح نیست.
بررسی گزینه 4): سیستمی تغییرناپذیر با زمان است که رفتار و مشخصات سیستم با زمان تغییر نکند. یعنی رابطه‌ی ورودی و خروجی آن مستقل از زمان (نامتغیر با زمان) باشد.
میتوان بیان کرد که در یک سیستم تغییرناپذیر با زمان اگر پاسخ سیستم به ورودی $x(t)$ برابر با $y(t)$ باشد آن‌گاه پاسخ به ورودی $x(t-t_0)$ برابر با $y(t-t_0)$ خواهد بود، یعنی اگر $T\{x(t) \} =y(t)$ باشد، آن‌گاه $T\{x(t-t_0) \} = y(t-t_0)$ است.
برای سیستم پیوسته $y\left(t\right)=\frac{2}{x^2\left(t\right)-1}$
$\left\{ \begin{array}{c}T\left\{x\left(t-t_0\right)\right\}=\frac{2}{x^2\left(t-t_0\right)-1} \\ y\left(t-t_0\right)=\frac{2}{x^2\left(t-t_0\right)-1}\ \ \ \ \ \ \end{array} \begin{array}{cc}{{\ \ \ \ \stackrel{T\left\{x\left(t-t_0\right)\right\}=y\left(t-t_0\right)}{\longrightarrow}}} & \text{سیستم}\mathrm{\ }\text{تغییرناپذیر}\mathrm{\ }\text{با}\mathrm{\ }\text{زبان}\mathrm{\ }\text{است }\end{array}\right. $
برای سیستم گسسته $y\left[n\right]=\left(n+1\right)2^{x\left[n\right]}$
$\left\{ \begin{array}{c}T\left\{x\left[n-n_0\right]\right\}=\left(n+1\right)2^{x\left[n-n_0\right]} \\ y\left[n-n_0\right]=\left(n-n_0+1\right)2^{x\left[n-n_0\right]} \end{array} \begin{array}{cc}\ \ \ \ {{\stackrel{T\left\{x\left[n-n_0\right]\right\}\neq y\left[n-n_0\right]}{\longrightarrow}}} & \text{سیستم}\mathrm{\ }\text{تغییرپذیر}\mathrm{\ }\text{با}\mathrm{\ }\text{زمان}\mathrm{\ }\text{است }\end{array}\right.$
سیستم پیوسته تغییرناپذیر با زمان است اما سیستم گسسته تغییرپذیر با زمان است؛ درنتیجه این گزینه صحیح نیست.
گزینه 1 درست است.
متوسط اگر ضرایب سری فوریه سیگنال $x(t)$ را $a_k$ درنظر بگیریم، ضرایب سری فوریه سیگنال $y(t)=x(2+3t)$ برحسب $a_k$ کدام است؟ (دوره تناوب سیگنال $x(t)$، برابر 2 است.) سری فوریه
گزینه‌ی 2 صحیح است
فرکانس اصلی سیگنال $x(t)$ برابر با $w_0=\frac{2\pi}{T}=\frac{2\pi}{2}=\pi$ می‌باشد.
برای رسیدن به $x(2+3t)$ از روی $x(t)$ به‌شکل زیر عمل می‌کنیم:
$\genfrac{}{}{0pt}{}{x\left(t\right){{\stackrel{t\to t+2}{\longrightarrow}}}}{\text{خاصیت}\mathrm{\ }\text{انتقال}\mathrm{\ }\text{زمانی}} \begin{array}{c} \ \ \ \ x\left(t+2\right){{\stackrel{t\to 3t}{\longrightarrow}x\left(3t+2\right)}} \end{array}$
$a_k{{\stackrel{\times e^{jk\pi \times \left(2\right)}}{\longrightarrow}{a_{k}}e^{2jk\pi }{{\stackrel{\text{بدون}\mathrm{\ }\text{تغییر}}{\longrightarrow}{a_{k}}e^{2jk\pi }}}}}$
درنتیجه گزینه‌ی 2 صحیح است.
دشوار اگر $H\left(e^{j\omega }\right)=\left\{ \begin{array}{c}{\mathrm{cos} \left(\omega \right)\ }\ \ \ \ 0\le \omega \le \frac{\pi }{2} \\ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\pi }{2}\le \omega \le \pi \end{array}\right.$ پاسخ فرکانسی سیستم 1 با پاسخ ضربه $h_1\left[n\right]$ باشد و پاسخ ضربه سیستم 2 به‌صورت $h_2\left[n\right]={\left(-1\right)}^nh_1\left[h\right]$ باشد، در مورد سیستم 2 چه میتوان گفت؟ سیستم‌های LTI
گزینه 4 صحیح است.
فیلتر، سیستمی LTI با پاسخ فرکانسی $H(w)$ می‌باشد که معمولاً با هدف تأثیرگذاری برروی فرکانس‌های سیگنال ورودی طراحی می‌شود.
برای مثال فیلتر زمان گسسته بالاگذر فیلتری است که فرکانس‌های پایین (فرکانس‌های حول مضارب زوج $\pi$ مانند $0$ و $\pm 2\pi$ و $\pm 4\pi$) را عبور نمی‌دهد و فرکانس‌های بالا (فرکانس‌های مضارب فرد $\pi$ مانند $\pi$ و $\pm 3\pi$) را عبور می‌دهد. باتوجه به این‌که در حالت زمان گسسته فرکانس‌های موهومی خاصیت تناوبی دارند $|H(w)|$ فیلتر زمان گسسته بالاگذر به‌شکل زیر است. $w_c$ فرکانس قطع سیستم می‌گویند.
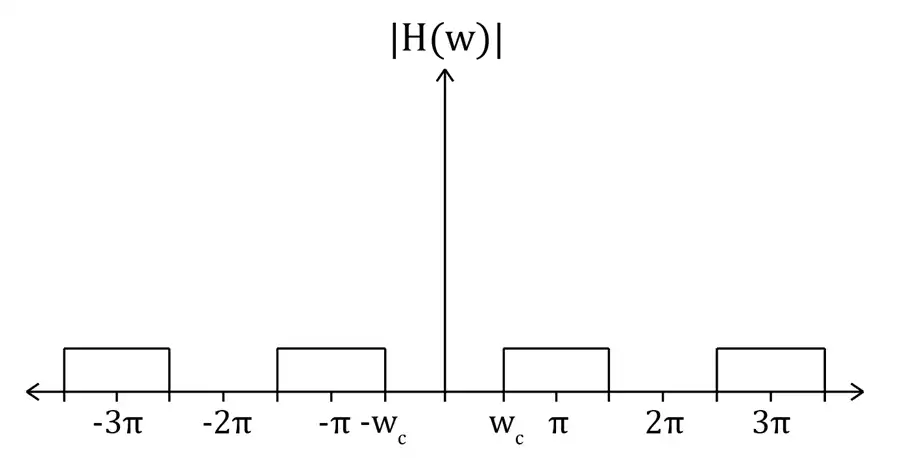
حال برای حل سؤال باید نوع فیلتر خواسته شده را مشخص کنیم:
$H\left(c^{jw}\right)=\left\{ \begin{array}{c} {\mathrm{cos} \left(w\right)\ }\ \ \ \ \ \ \ 0\le \left|w\right|\le \frac{\pi }{2}\to 0\le w\le \frac{\pi }{2},-\frac{\pi }{2}\le w\le 0\to -\frac{\pi }{2}\le \ w\le \frac{\pi }{2} \\ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\pi }{2}\le \left|w\right|\le \pi \to -\frac{\pi }{2}\le w\le -\pi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \end{array}\right.$
حال باید برای حل سؤال نوع فیلتر خواسته شده را مشخص کنیم. در سیستم 1 داریم:
$H\left(c^{jw}\right)=\left\{ \begin{array}{c} {\mathrm{cos} \left(w\right)\ }\ \ \ \ \ \ \ 0\le \left|w\right|\le \frac{\pi }{2}\to \ \ \ \ -\frac{\pi }{2}\le w\le \frac{\pi }{2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\pi }{2}\le \left|w\right|\le \pi \ \ \ \ \ \ \ \ -\pi \le w\le -\frac{\pi }{2},\frac{\pi }{2}\le w\le \pi \ \ \ \ \ \ \ \ \ \ \end{array} \right.$
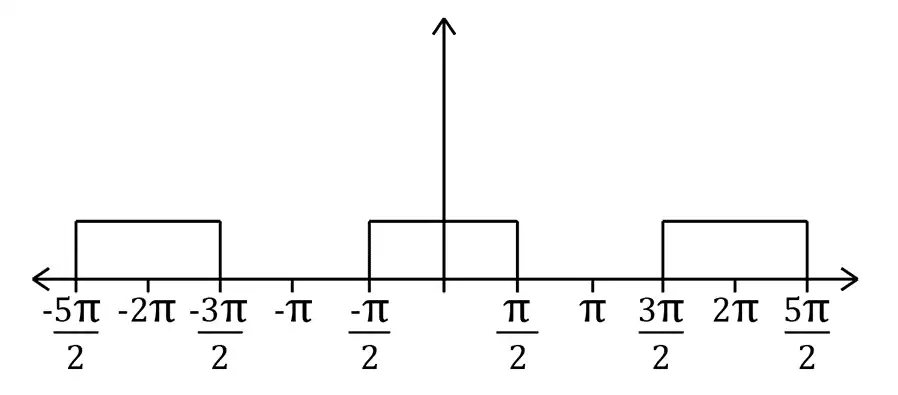
سیستم 1 یک فیلتر پایین‌گذر است. البته توجه کنید که شکل رسم شده تقریب مقدار $cos(w)$ در بازه‌ی $-\frac{\pi }{2}\le \ w\le \frac{\pi }{2}$ که به‌غیر $\frac{\pi }{2}$ و $-\frac{\pi }{2}$ مقدار 0 دیگری ندارد و برای ساده‌سازی مقدار $H\left(c^{jw}\right)$ در بازه‌ی $-\frac{\pi }{2}\le \ w\le \frac{\pi }{2}$ مقدار ثابت فرض شده.
در سیستم 2 داریم:
$h_2\left[n\right]={\left(-1\right)}^nh_1\left[n\right]$
که میتوان نوشت:
$h_2\left[n\right]=e^{j\pi n}h_1\left[n\right]$
که بنابر خاصیت زیر:
$\pi \left(n\right)e^{jw_0n}{{\stackrel{F}{\leftrightarrow}}}\pi \left(w-w_0\right)$
پس داریم:
$\pi \left[n\right]e^{j\pi n}{{\stackrel{F}{\leftrightarrow}\pi \left(w-\pi \right)}}$
پس میتوان گفت سیستم 2 انتقال‌یافته سیستم 1 به‌اندازه‌ی $\pi$ است.
درنتیجه $|H(w)|$ سیستم 2 به‌شکل زیر است.
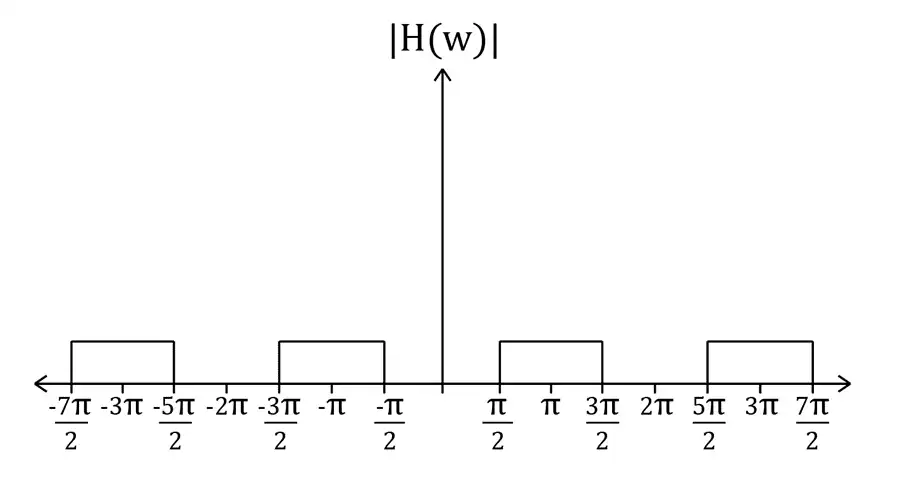
که فیلتر بالاگذر است و زیرفرکانس‌های پایین را عبور نمی‌دهد و فرکانس‌های بالا را عبور می‌دهد.
گزینه 4 صحیح است.
متوسط تابع تبدیل سیستمی، به شرح رو‌به‌رو است. تبدیل لاپلاس
$H\left(s\right)=\frac{s-2}{s^2+s-2}$
کدام مورد درخصوص این سیستم، نادرست است؟
راه‌حل اول:
گزینه 2 صحیح است.
$H\left(s\right)=\frac{s-2}{s^2+s-2}=\frac{s-2}{\left(s+2\right)\left(s-1\right)}$
دارای دو قطب در $s=-2$ و $s=1$ است.
باتوجه به خاصیت $ROC$ و تابع $H(s)$ سه ناحیه $ROC$ برای $H(s)$ میتوان متصور نمود:
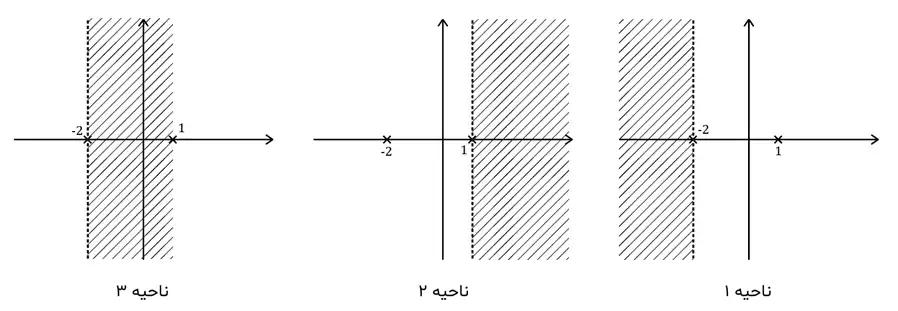
برای عِلّی بودن باید $s=+\infty$ در ناحیه همگرایی قرار داشته باشد. برای برقراری این شرط، شرط لازم این است که $s$ تا منتهی‌الیه سمت راست صفحه $s$ برود؛ که فقط ناحیه 1 همچین شرایطی دارد. بقیه ناحیه‌ها غیرعِلّی هستند.
برای پایدار بودن $s$ شرط لازم این است محور $\left(RC\left[s\right]=0\right) jw$ در ناحیه همگرایی $ROC$ باشد که فقط ناحیه 3 این خاصیت را دارد. بقیه ناحیه‌ها ناپایدار هستند.
باتوجه به توضیحات داده شده هیچکدام از 3 ناحیه گفته شده نمیتواند شرایط لازم عِلّی بودن و پایدار بودن را داشته باشد. در نتیجه گزینه 3 صحیح است.
راه‌حل دوم:
با توجه به تابع تبدیل داده شده قطب های تابع تبدیل به صورت 1=s و 2-=s هستند، لذا میتوان سه ناحیه همگرایی برای آن در نظر گرفت به ترتیب به بیان حالات مد نظر میپردازیم، در صورتی که ناحیه همگرایی 1<Roc باشد چون دست راستی است لذا سیستم علی بوده و چون محور موهومی را در بر نمیگیرد (تبدیل فوریه ندارد) ناپایدار است. همینجا مشخص است که گزینه 2 که گفته علی و پایدار نادرست است چون در صورتی که علی باشد حتما ناپایدار است و درسوال گزینه نادرست خواسته شده است. برای آموزش بیشتر به بررسی بقیه گزینه ها میپردازیم در صورتی که 1>Roc و 2-<Roc
(بین 1و 2- باشد) چون محور موهومی را در بر میگیرد پس پایدار است و به علت این که دست راستی نیست نمیتواند علی باشد. (رد گزینه 4) و در ناحیه آخر هم به علت دست چپی بودن و در بر نداشتن محور موهومی غیر علی و ناپایدار است.
پلتفرم آزمون درس سیگنال و سیستمها
پلتفرم آزمون و بانک تست و مجموعه سوالات کنکور ارشد کامپیوتر، آی‌تی و علوم کامپیوتر
سیستم قدرتمند آزمون کنکور کامپیوتر - اولین و تنها سیستم آزمون رشته کامپیوتر
داوطلبین کنکور ارشد کامپیوتر، آی‌تی و علوم کامپیوتر، با این پلتفرم نیازی به تهیه هیچ کتابی ندارید، بهتر از هر کتاب مجموعه سوالات
پلتفرم آزمون
امکانات پلتفرم
- بیش از 10000 تست تالیفی و کنکور
- پاسخ تشریحی تست‌های 24 سال اخیر کنکور ارشد کامپیوتر و آی‌تی
- پاسخ تشریحی تست‌های 15 سال اخیر کنکور ارشد علوم کامپیوتر
- بیش از 2000 سوال تالیفی از مراجع با پاسخ تشریحی
- شبیه سازی کنکورهای سراسری سال‌های گذشته
- منتخب کردن تست‌ها قبل، بعد و در حین آزمون
- فیلترهای فوق هوشمند برای انتخاب سوالات
- ایجاد آزمون از هر فصل یا از هر درس
- ایجاد آزمون واش بک و فیدبک
- همچنین آماده شده برای کنکورهای کاردانی کامپیوتر و دکتری هوش مصنوعی
پلتفرم آزمون علاوه بر تمامی تست‌های سال‌های گذشته ویژگی‌های متمایز‌کننده دیگری نیز دارد، مانند رقابت با سایر دانشجویان، دسترسی به سؤالات تألیفی، امکان ایجاد آزمون شخصی‌سازی شده و…. برای آشنایی بیشتر با پلتفرم آزمون و ثبت‌نام در آن، به صفحه پلتفرم آزمون کنکور کامپیوتر مراجعه کنید.
مطالب مرتبط
همه مقالات
