برای شروع حرفهای کنکور ارشد کامپیوتر،آیتی و علوم کامپیوتر حتما روی عکس زیر کلیک کنید تا در کانال کنکور کامپیوتر عضو شوید، در این کانال به معرفی بهترین منابع کنکور ارشد،برنامه ریزی و مشاوره، معرفی گرایشها و هر آنچه برای موفقیت در کنکور ارشد نیاز دارید پرداخته شده است

مرتبسازیها از الگوریتمهای بسیار پرکاربرد در دنیای ماشینها و کامیپوترها هستند. مرتبسازی یا Ordering ساختمان دادهای را برای نمایش مرتب و ساختارمند دادهها فراهم میکند که باعث میشود اعمالی نظیر جستجوی دادهها بسیار بهینهتر صورت بگیرد. دراین مقاله قصد داریم یکی از روشهای مرتبسازی به نام مرتب سازی ادغامی یا Merge sort را شرح دهیم.
مرتب سازی ادغامی چیست؟
مرتب سازی ادغامی یکی از روشهای مرتبسازی مبتنی بر تقسیم و غلبه (Divide & Conqure) است مسئله را به زیر مسئلههای کوچکتر تبدیل میکند و سپس آنرا حل میکند. فرض کنید یک آرایهی n عضوی از عناصر را دراختیار داریم. این آرایه را به 2 قسمت مساوی تقسیم میکنیم. در این حالت 2 آرایه $\frac{n}{2}$ عضوی داریم.
مجددا هرکدام از این آرایهها را به دو بخش تقسیم میکنیم و آنقدر این عمل را ادامه میدهیم تا به آرایههای تک عنصری برسیم. در هنگام تقسیم شدن آرایه به دو آرایه، عملیات ادغام انجام شده و هرنیمه مرتب میشود و درنهایت یک آرایه مرتبشده از عناصر را دراختیار داریم. مرتبه اجرایی مرتب سازی ادغامی از O(n logn) است. درادامه هدف ما آموزش الگوریتم مرتب سازی ادغامی است که بهصورت کامل شرح داده میشود.
در صورتیکه به این مقاله علاقهمند هستید، ممکن است صفحات زیر نیز برای شما جذاب باشد:
- آموزش جامع مرتب سازی سریع
- آموزش جامع مرتب سازی حبابی
- آموزش جامع مرتب سازی درجی
الگوریتم مرتب سازی ادغامی
همانطور که اشاره شد، این روش مرتبسازی برگرفته از تقسیم و غلبه است که به صورت بازگشتی برروی آرایه اعمال میشود. برای توضیح این الگوریتم، درابتدا مثالی را بررسی میکنیم که با این الگوریتم آشنایی پیدا کنیم.
فرض کنید آرایه از عناصر به شکل زیر داریم :
| $11$ | $2$ | $10$ | $14$ | $40$ | $1$ | $8$ | $20$ |
حال میخواهیم اعداد درون این آرایه را مرتب کنیم. همانطور که گفته شده درابتدا آرایه را به دو آرایه $\frac{n}{2}$ عضوی تقسیم میکنیم :
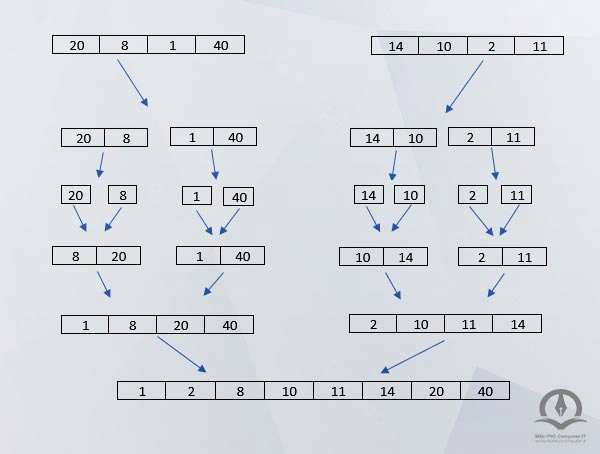
همانطور که مشاهده میشود، توانستیم به روش بازگشتی آرایه را به 8 آرایه تک عضوی تقسیم کنیم و سپس هر دو آرایه تک عضوی را با یکدیگر مقایسه میکنیم و آرایههای 2 عضوی ایجاد میکنیم، اینکار تا زمانی که یک آرایه 8 عنصری داشته باشیم، ادامه مییابد.
پس میتوان الگوریتمی به شکل زیر برای آن ارائه داد :
- شروع
- یک آرایه با نام array و شماره خانهی چپ و راست به نام L و N را دریافت کن (یک آرایه با L-N عنصر داریم).
- تابع با نام merge را فراخوانی کن :
if (L < R) mid=(L+N) / 2 mergesort(array, L, mid) mergesort(array, mid+1, R) merge(array, left, mid, right) - اتمام
تحلیل الگوریتم مرتب سازی ادغامی
حال در خصوص تحلیل الگوریتم مرتب سازی ادغامی به شیوهی زیر عمل میکنیم :
- درابتدا یک آرایه که قرار است مرتب شود را دریافت و ذخیره میکنیم. سپس مقدار عنصر چپ که $0$ و عنصر n است را در متغیرهای L,N ذخیره میکنیم.
- یک تابع با نام merge را صدا میزنیم. در این تابع در ابتدا بررسی میکنیم که حتما عنصر چپ از عنصر راست بزرگتر باشد تا تابع اجرا شود.
- در خط بعد توسط mid = (L+N)/2 شماره خانه عنصر میانه آرایه را محاسبه و درون mid ذخیره میکنیم.
- توسط دو خط بعدی و توسط mergesort نیمه ابتدایی و انتهایی آرایه مجددا به همین تابع بازگشت میدهیم و در خط بعدی، توسط تابع merge که مرتبه زمانی آن برابر با $O(n)$ است، آرایهها را در هم ادغام میکنیم.
تابع merge عمل ادغام دو آرایه مرتب را انجام می دهد. در بخش قبل، مشاهده کردید که آرایهها در هم ادغام میشوند و یک آرایه مرتب میسازند، مجددا این آرایههای مرتب در هم ادغام میشوند تا درنهایت یک آرایهی تمام مرتب بسازند. اما باچه الگوریتم و با چه مرتبه زمانی میتوان این آرایهها را درهم ادغام کرد؟
در پاسخ به این سوال درابتدا دو آرایه 4 عنصری مرتب را با یکدیگر ادغام میکنیم :
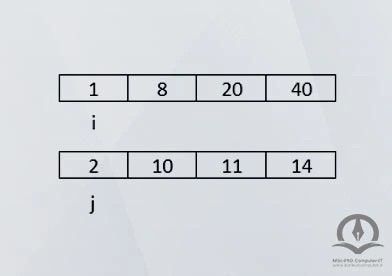
دو اندیس i,j داریم که هرکدام به خانهی صفرم آرایهها اشاره میکنند. درصورتی که عدد موجود در خانهی اندیس i که در اینجا عدد 1 است، از عدد موجود در خانهی اندیس j که در اینجا 2 است، کوچکتر باشد، خانهی شماره iام آرایه را به لیست جدید اضافه میکنیم و i به خانهی بعدی منتقل میشود و j در همانجا باقی میماند و یا بالعکس.
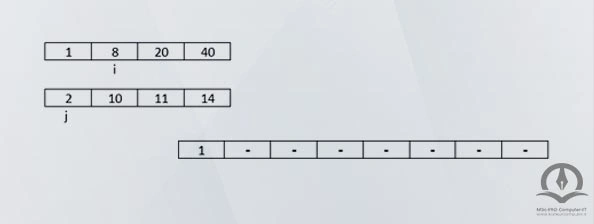
همانطور که مشاهده میشود، عدد 1 به آرایه 8 عنصری اضافه شد و اگر این روند تا انتها ادامه دهیم، خواهیم دید که آرایه بهطور کامل مرتب میشود.
حال تعداد مقایسات در اینجا، مرتبه زمانی این الگوریتم را مشخص میکنند.
حداقل مقایسه : (n , m)min حداکثر مقایسه : 1 – m + n
m و n طول دو آرایه را مشخص میکنند.
لذا مرتبه زمانی این کد از O(m+n) خواهد بود.
شبه کد مرتب سازی ادغامی
بعد از بررسی الگوریتم مرتب سازی ادغامی، باید شبه کدی از آن را بررسی کنیم تا دید بازتری به الگوریتم آن داشته باشیم. شبه کد الگوریتم مرتب سازی ادغامی تقریبا همانند الگوریتمی است که ذکر شد.
function MergeSort (array , L , R)
mid = 0
begin
if (L < R) then
begin
mid = (L+R) / 2
Merge Sort (array, L , mid)
Merge Sort (A, mid + 1 , R)
Merge (A, mid, L, R)
end
end
در ادامه نحوهی پیاده سازی الگوریتم مرتب سازی ادغامی در جاوا و پایتون را بررسی میکنیم.
مرتبسازی ادغامی در جاوا
حال یک نمونه از کد مرتب سازی ادغامی را با زبان جاوا بررسی میکنیم. برای اجرای این قطعه کدها میتوانید از کامپایلرهای آنلاین و یا IDEهای معروف مانند Intellij استفاده کنید. نحوه ی پیاده سازی مرتب سازی ادغامی با تابع mergesort در جاوا به شرح زیر است :
public class Main {
public static void main(String[] args) {
int [] array = {20, 8, 1, 40, 14, 10, 2, 11};
mergesort(array, 0, array.length-1);
printArray(array);
}
public static void mergesort (int [] array, int L, int R) {
if (L < R) {
int mid = L + (R - L) / 2;
mergesort(array, L, mid);
mergesort(array, mid+1, R);
merge(array,L , mid, R);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
public static void merge (int [] array, int L, int mid, int R) {
int a1 = mid - L + 1;
int a2 = R - mid;
int[] leftArray = new int[a1];
int[] rightArray = new int[a2];
for (int i = 0; i < a1; i++)
leftArray[i] = array[L + i];
for (int j = 0; j < a2; j++)
rightArray[j] = array[mid + 1 + j];
int i = 0, j= 0 ;
int k = L;
while (i < a1 && j < a2) {
if (leftArray[i] <= rightArray[j]) {
array[k] = leftArray[i];
i++;
} else {
array[k] = rightArray[j];
j++;
}
k++;
}
while (i < a1) {
array[k] = leftArray[i];
i++;
k++;
}
while (j < a2) {
array[k] = rightArray[j];
j++;
k++;
}
}
}
مرتب سازی ادغامی در ++C
حال این کد را با زبان c++ مینویسیم و برای تست این کد میتوانید از کامپایلرهای آنلاین استفاده کنید. نحوه ی پیاده سازی مرتب سازی ادغامی در c++ به شکل زیر است.
#include <iostream>
using namespace std;
// Merges two subarrays of array[].
// First subarray is arr[begin..mid]
// Second subarray is arr[mid+1..end]
void merge(int array[], int const left, int const mid,
int const right)
{
auto const subArrayOne = mid - left + 1;
auto const subArrayTwo = right - mid;
// Create temp arrays
auto *leftArray = new int[subArrayOne],
*rightArray = new int[subArrayTwo];
// Copy data to temp arrays leftArray[] and rightArray[]
for (auto i = 0; i < subArrayOne; i++)
leftArray[i] = array[left + i];
for (auto j = 0; j < subArrayTwo; j++)
rightArray[j] = array[mid + 1 + j];
auto indexOfSubArrayOne
= 0, // Initial index of first sub-array
indexOfSubArrayTwo
= 0; // Initial index of second sub-array
int indexOfMergedArray
= left; // Initial index of merged array
// Merge the temp arrays back into array[left..right]
while (indexOfSubArrayOne < subArrayOne
&& indexOfSubArrayTwo < subArrayTwo) {
if (leftArray[indexOfSubArrayOne]
<= rightArray[indexOfSubArrayTwo]) {
array[indexOfMergedArray]
= leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
}
else {
array[indexOfMergedArray]
= rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
}
indexOfMergedArray++;
}
// Copy the remaining elements of
// left[], if there are any
while (indexOfSubArrayOne < subArrayOne) {
array[indexOfMergedArray]
= leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
indexOfMergedArray++;
}
// Copy the remaining elements of
// right[], if there are any
while (indexOfSubArrayTwo < subArrayTwo) {
array[indexOfMergedArray]
= rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
indexOfMergedArray++;
}
delete[] leftArray;
delete[] rightArray;
}
// begin is for left index and end is
// right index of the sub-array
// of arr to be sorted */
void mergeSort(int array[], int const begin, int const end)
{
if (begin >= end)
return; // Returns recursively
auto mid = begin + (end - begin) / 2;
mergeSort(array, begin, mid);
mergeSort(array, mid + 1, end);
merge(array, begin, mid, end);
}
// UTILITY FUNCTIONS
// Function to print an array
void printArray(int A[], int size)
{
for (auto i = 0; i < size; i++)
cout << A[i] << " ";
}
// Driver code
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
auto arr_size = sizeof(arr) / sizeof(arr[0]);
cout << "Given array is \n";
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
cout << "\nSorted array is \n";
printArray(arr, arr_size);
return 0;
}
مرتب سازی ادغامی در پایتون
در این بخش میخواهیم الگوریتم مرتب سازی ادغامی در پایتون را بررسی کنیم و کد مربوط بهآن را پیادهسازی کنیم. کدآن را میتوانید در کامپایلرهای آنلاین مانند repl.it و یا IDEهای موجود مانند PyCharm، VS code و ... تست کنید. نحوه ی پیاده سازی مرتب سازی ادغامی با پایتون به شکل زیر است :
def merge(array, leftArray, rightArray):
i = j = k = 0
while i < len(leftArray) and j < len(rightArray):
if leftArray[i] < rightArray[j]:
array[k] = leftArray[i]
i += 1
else:
array[k] = rightArray[j]
j += 1
k = k + 1
while i < len(leftArray):
array[k] = leftArray[i]
k += 1
i += 1
while j < len(rightArray):
array[k] = rightArray[j]
k += 1
j += 1
def mergesort(array):
if len(array) > 1:
mid = len(array) // 2
leftArray = array[:mid]
rightArray = array[mid:]
mergesort(leftArray)
mergesort(rightArray)
merge(array, leftArray, rightArray)
array = [20, 8, 1, 40, 14, 10, 2, 11]
mergesort(array)
print(array)
خروجی کد بالا به شکل زیر میباشد :
[$40$,$20$,$14$,$11$,$10$,$8$,$2$,$1$]
دو قطعه کدی که به زبانهای جاوا و پایتون نوشته شد، دقیقا همان آرایهای است که در مثال بالا ذکر کردیم و دقیقا همان آرایه، ازطریق این کدها مرتب شد.
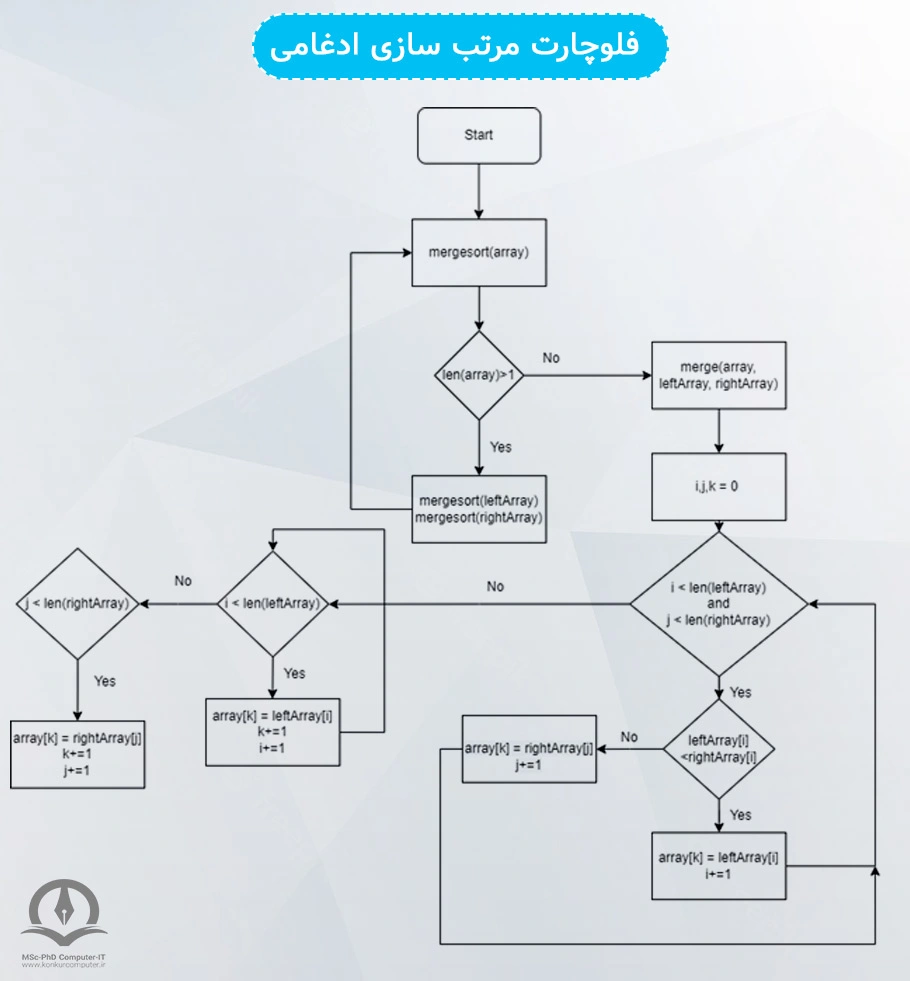
فلوچارت مرتب سازی ادغامی
برای درک بهتر کدهای نوشته شده، بهتر است که فلوچارت آنرا بررسی کنیم تا دید گستردهتری نسبت به کدهای آن داشته باشیم. فلوچارت مرتب سازی ادغامی در پایتون به شکل زیر است.
مرتبه زمانی مرتب سازی ادغامی
اصولا پیچیدگی زمانی یک الگوریتم را توسط پرتکرارترین جمله بررسی میکنند. در الگوریتم مرتب سازی ادغامی ما میتوانیم یک تابع بازگشتی برای محاسبه میزان پیچیدگی بنویسیم. تابع پیچیدگی زمانی الگوریتم mergesort به شرح زیر است :
T(n) = 2T($\frac{n}{2}$) + O(n)
حال قبل از اینکه به تحلیل این رابطه بپردازیم، باید چگونگی بدست آمدن این تابع را بررسی کنیم.
- T(n) تابعی است که به عنوان مرتبه زمانی کد در نظر میگیریم. مقدار n همان مقدار سایز آرایه است و مقادیر مختلفی دارد.
- $T(\frac{n}{2})$ تابعی است که مجددا تابع T(n) را با مقدار ورودی $\frac{n}{2}$ فراخوانی میکند. باتوجه به الگوریتمی که شرح داده شد، مقدار آرایه درهر مرحله نصف میشود و این تا زمانی ادامه مییابد که که مقدار n برابر با یک شود. حال ما داریم مرتبه زمانی این الگوریتم را بررسی میکنیم و چون آرایه به دو بخش $\frac{n}{2}$ تایی تقسیم میشود، ضریب 2 را برای $T(\frac{n}{2})$ قرار میدهیم.
- $O(n)$ میزان مقایساتی است که در هرمرحله برای ادغام دو آرایه مرتب انجام میدهیم.
حال که این تابع را نوشتیم، برای بررسی مرتبه زمانی آن از روش معروف Master استفاده میکنیم که در این صورت مرتبه زمانی کد ما برابر با n.logn خواهد بود.
الگوریتمهای مرتب سازی دارای بدترین، متوسط و بهترین زمان اجرا هستند. خوشبختانه الگوریتم مرتب سازی ادغامی در سه حالت فوق، دارای مرتبه زمانی n.logn میباشد که براساس اثباتهایی که تاکنون انجام شده، هیچ روش مقایسهای وجود ندارد که بتواند یک آرایه را در زمان کمتر از n.logn مرتب کند و بنابراین این از ویژگیهای خوب مرتب سازی ادغامی است.
مزایا و معایب مرتب سازی ادغامی
از مزایا و ویژگی های مرتب سازی ادغامی، مرتبه زمانی خوب آن است. زیرا در همهی حالات، زمان مشابهی دارد و این زمان معادل با مینیمم زمانی است که هر الگوریتم مقایسهای، برای مرتبسازی از آن استفاده میکند.
از عیبهای مرتب سازی ادغامی، استفاده آن از حافظه است. زیرا در هرمرحله آرایههای جدیدی ساخته میشوند و حافظه را اشغال میکنند. مرتبه حافظه مرتب سازی ادغامی از O(n) است.
مقایسه مرتب سازی ادغامی با سایر مرتب سازی ها
جدول زیر برخی از انواع روشهای مرتبسازی را براساس مرتبه زمانی الگوریتمهایشان، مقایسه میکند.
| روش مرتبسازی | بهترین حالت | حالت متوسط | بدترین حالت | توضیحات |
|---|---|---|---|---|
| انتخابی (selection sort) | O(n2) | O(n2) | O(n2) | غیرمتعادل - درجا |
| حبابی | O(n2) | O(n2) | O(n2) | متعادل - درجا |
| حبابی بهینه | O(n) | O(n2) | O(n2) | متعادل - درجا |
| ادغامی (Merge sort) | O (n log n) | O (n log n) | O (n log n) | متعادل- غیردرجا |
| درجی | O(n) | O(n2) | O(n2) | متعادل - درجا |
| سریع | O (n log n) | O (n log n) | O(n2) | غیرمتعادل - درجا |
منظور از "درجا" در این جدول، عدم استفاده از آرایههای اضافی است که فقط در مرتب سازی ادغامی این عمل اتفاق میافتد و همچنین منظور از "متعادل" این است که اگر دو عدد تکراری پشت سرهم داشته باشیم، آن اعداد تکراری با یکدیگر جابهجا نشوند.
نمونه سوالات مرتب سازی ادغامی
مثال 1 : بدترین، متوسط و بهترین پیچیدگی زمانی الگوریتم mergesort، چه نوع تابعی است؟
- بدترین : O(n2) - متوسط : O(n2) - بهترین : O(n Log n)
- بدترین : O(n Log n) - متوسط : O(n Log n) - بهترین : O(n Log n)
- بدترین : O(n2) - متوسط : O(n Log n) - بهترین : O(n Log n)
- بدترین : O(n2 Log n) - متوسط : O(n2) - بهترین : O(n Log n)
پاسخ : براساس موارد ذکر شده، گزینه 2 پاسخ است.
مثال 2 : پیچیدگی حافظه مرتب سازی ادغامی چیست؟
- O(n2)
- O(n Log n)
- O(n)
- O(logn)
پاسخ : براساس موارد ذکر شده گزینه 3 پاسخ است.
مثال 3 : فرض کنید الگوریتم جدیدی از مرتب سازی ادغامی را ارائه داده ایم. در این الگوریتم آرایه را به 4 قسمت مساوی تقسیم میکنیم و این عمل را آنقدر ادامه میدهیم تا به آرایههای تک عنصری برسیم. سپس عمل ادغام برروی چهار آرایه انجام میشود. مرتبه زمانی این کد چه میزان خواهد بود؟
- O(n2)
- O(n Log n)
- O(n2 Log n)
- O(n3)
پاسخ : درروش عادی مرتبسازی ادغامی، هربار دو آرایه مرتب را دریکدیگر ادغام میکردیم. در این مسئله ما نیاز داریم هربار 4 لیست مرتب را درهم ادغام کنیم. حال برای ادغام 4 لیست مرتب به چه میزان زمانی نیاز داریم؟
در ساختماندادهها، برای ادغام k لیست مرتب و ساخت یک لیست مرتب جدید، به میزان زمان n logk نیاز است که n مجموعه سایز تمام آرایهها است و این عمل توسط درخت minheap انجام میشود. حال برای ادغام 4 لیست مرتب، ما نیاز به زمان n log4 داریم که چون log4 یک عدد ثابت است، بنابراین مرتبه ادغام این 4 لیست از O(n) است. حال ما هربار آرایه را به 4 بخش مساوی تقسیم بندی میکنیم و بهصورت بازگشتی این عمل را ادامه میدهیم. بنابراین رابطه بازگشتی زمان این الگوریتم برابر با :
T(n) = 4T($\frac{n}{2}$) + O(n)
توسط رابطهی Master اثبات میشود که این الگوریتم از مرتبه O(n2) میباشد.
جمع بندی
مرتبسازی در دنیای کامپیوترها، از مهمترین مسائل است که دانشمندان کامپیوتر، زمان زیادی را برای ارائه الگوریتمهای آن صرف کردهاند. نکتهی مهمی که دراینباره وجود دارد، این است که توسط درخت تصمیم، اثبات میشود که هیچ الگوریتم مرتبسازی مقایسهای وجود ندارد که بتواند در زمان کمتر از n logn یک آرایه را مرتب کند. بنابراین چالش در مرتبسازی، افزایش سرعت و همچنین برابر کردن زمان اجرا در بدترین، متوسط و بهترین حالتهاست که خوشبختانه از مزیتهای مرتبسازی ادغامی، برابر بودن زمان اجرا در این سه حالت است و همچنین پیچیدگی حافظه مرتب سازی ادغامی، نسبت به سایر مرتبسازیها بیشتر است.
بهترین روش مرتبسازی کدام است؟
درپاسخ به این سوال باید بررسی کرد که خواستههای ما از مرتبسازی چیست. اگر خواستهی ما مصرف کمتر حافظه باشد، مرتبسازی ادغامی نمیتواند انتخاب خوبی باشد و بههمین علت، بسیاری از IDEهای معروف، از مرتب سازی سریعآموزش مرتب سازی سریع بصورت 0 تا 100 این صفحه مرتب سازی سریع را بصورت 0 تا 100 آموزش داده و مثال مرتب سازی سریع آورده شده است، همچنین بهترین، متوسط و بدترین حالت مرتب سازی سریع بررسی شده استفاده میکنند. هرچند امروزه روشهای بهینه شدهای برای مرتبسازیها ارائه شده که به افزایش سرعت و مصرف کمتر حافظه اشاره دارند و شاید خیلی از این روشها هنوز در کتابها موجود نباشد. بهعنوان مثال روشی که امروزه برای quick sort یا مرتبسازی سریع استفاده میشود. باعث میشود که در تمام حالات، مرتبهی زمانی در O(n logn) باشد.
این صفحه مرتب سازی سریع را بصورت 0 تا 100 آموزش داده و مثال مرتب سازی سریع آورده شده است، همچنین بهترین، متوسط و بدترین حالت مرتب سازی سریع بررسی شده استفاده میکنند. هرچند امروزه روشهای بهینه شدهای برای مرتبسازیها ارائه شده که به افزایش سرعت و مصرف کمتر حافظه اشاره دارند و شاید خیلی از این روشها هنوز در کتابها موجود نباشد. بهعنوان مثال روشی که امروزه برای quick sort یا مرتبسازی سریع استفاده میشود. باعث میشود که در تمام حالات، مرتبهی زمانی در O(n logn) باشد.
کاربرد مرتب سازی ادغامی در کجاست؟
این روش مرتبسازی کاربرد زیادی در مرتبسازی دارد که به شرح زیر هستند:
مرتبسازی linked listها را در O(n logn) انجام میدهند.
مرتبسازی linked listها بدون استفاده از حافظه خارجی انجام میشود.
برای شمارش تعداد وارونگیها دریک لیست مناسب هستند.








































