در این صفحه نمونه سوالات معماری کامپیوتر با پاسخ تشریحی برای شما عزیزان قرار داده شده است، سعی شده مثال های معماری کامپیوتر تمامی مباحث منطقی را در بر گیرد. در صورتی که علاقه دارید تا بیشتر با درس معماری کامپیوتر آشنا شوید و فیلم های رایگان معماری کامپیوتر را مشاهده کنید به صفحه معرفی و بررسی معماری کامپیوتر آموزش جامع معماری کامپیوتر
در مهندسی کامپیوتر، معماری کامپیوتر مجموعه‌ای از قوانین و روش‌هایی است که به چگونگی طراحی، کارکرد، سازماندهی و پیاده سازی (ساخت) سیستم‌های کامپیوتری می‌پردازد، در این صفحه به بررسی و آموزش کامل معماری کامپیوتر پرداخته شده است مراجعه کنید.
قبل از اینکه به ادامه این مقاله بپردازیم توصیه می‌کنیم که فیلم زیر که در خصوص تحلیل و بررسی درس معماری کامپیوتر است را مشاهده کنید، در این فیلم توضیح داده شده که فیلم درس معماری کامپیوتر برای چه افرادی مناسب است و همین طور در خصوص فصول مختلف درس معماری کامپیوتر و اهمیت هر کدام از فصول آن صحبت شده است.
در ادامه این مقاله فیلم های رایگان معماری کامپیوتر که به آنها نیاز دارید نیز در اختیارتان قرار گرفته است.
فیلم های رایگان آموزش معماری کامپیوتر که به آنها نیاز دارید
در حال حاضر فیلم آموزش معماری کامپیوتر استاد رضوی پرطرفدارترین و پرفروش‌ترین فیلم آموزشی معماری کامپیوتر کشور است و هر سال حدود ۶۰۰۰ نفر این فیلم را تهیه می‌کنند
خرید فیلم های کامل معماری کامپیوتر
ویدیو درس معماری کامپیوتر
تخفیف سه ماه طلایی تا ۳ آبان
30% ویدیو نکته و تست معماری کامپیوتر
تخفیف سه ماه طلایی تا ۳ آبان
30%نمونه سوالات محاسبات درس معماری کامپیوتر
در زیر نمونه سوالات درس معماری کامپیوتر با پاسخ تشریحی را برای شما دانشجویان عزیز گردآوری کرده‌ایم، نمونه سوالات معماری کامپیوتر به گونه‌ای انتخاب شدند که همه نیازهای شما عزیزان را بر طرف کند.
(فرض کنید فقط گیت‌های ۲ ورودی در اختیار داریم و تاخیر هر یک ${\mathrm{5}}^{ns}$ باشد.)محاسبات
مدار جمع کننده BCD یک رقمی بصورت مقابل است.
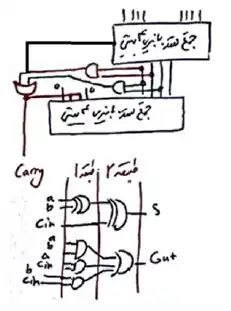
با توجه به آنچه که در نکته و تست معماری استاد رضوی که در تست شماره 14 فصل محاسبات گفته شده است، نکته زیر را می‌دانیم:
نکته: در صورتی که مجاز به استفاده از گیت‌های دو ورودی و بیشتر باشیم تاخیر کری BCD Adder اول $\mathrm{10}\mathrm{t}$ و تاخیر Sumاش $\mathrm{16}\mathrm{t}$ است، اما از BCD دوم تا آخر تاخیر کری $\mathrm{9}\mathrm{t}$ و تاخیر Sumها $\mathrm{15}\mathrm{t}$ است. حال در صورتی که مجاز به استفاده از گیت‌های دو ورودی نباشیم تاخیر کری BCD Adder اول $\mathrm{11}\mathrm{t}$ و تاخیر Sumاش $\mathrm{17}\mathrm{t}$ است، اما از BCD دوم تا آخر تاخیر کری $\mathrm{10}\mathrm{t}$ و تاخیر Sumها $\mathrm{16}\mathrm{t}$ است.
تاخیر جمع کننده‌های باینری ۴ بیتی بصورت CRA برابر تاخیر (۴ تا FA) می‌باشد، یعنی $(8tg)$
از آنجا که در مسیر کری، گیت or سه ورودی داریم و با توجه به اینکه در صورت سوال گفته شده است که فقط از گیت‌های ۲ ورودی می‌توانیم استفاده کنیم، لذا باید به دو تا گیت or دو ورودی تغییر یابد.
تاخیر کری در این جمع کننده یک رقمی BCD، $\mathrm{11}tg$ است.
تاخیر sum در این جمع کننده یک رقمی BCD، $\mathrm{11}tg$ است.
جمع کننده رقم دوم BCD می‌تواند به محض آماده شدن carry کارش را شروع کند لذا
$\mathrm{11}tg+\mathrm{16}tg=\mathrm{27}tg$
$\mathrm{27}\mathrm{\times }\mathrm{5}\mathrm{ns}\mathrm{=135}\mathrm{ns}$
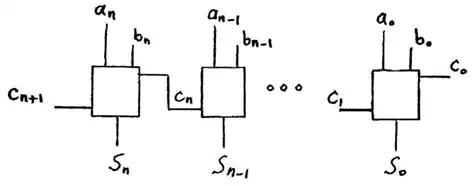
الف) $v = {a_n}.{b_n}.{\overline c _n} + {\overline a _n}.{\overline b _n}.{c_n}$
ب) $v = {c_n}\, \oplus \,{s_n}$
ج) $v = {a_n}.{b_n}.{s_n} + {\overline a _n}.{\overline b _n}.{\overline s _n}$
د) $v = {c_n}\, \oplus \,{c_{n + 1}}$
ما می دانیم روش های تشخیص Overflow در جمع مکمل 2
$\left\{ \begin{array}{c} \textrm{1}\ V=\overline{a_{n-1}}\overline{b_{n-1}}\genfrac{}{}{0pt}{}{\oplus }{+}a_{n-1}b_{n-1}\overline{S_{n-1}} \\ \textrm{2}\ V=\overline{a_{n-1}}\overline{b_{n-1}}C_{n-1}\genfrac{}{}{0pt}{}{\oplus }{+}a_{n-1}b_{n-1}\overline{C_{n-1}} \\ \textrm{3}\ V=C_n\oplus C_{n-1} \end{array}\right.$
$\Leftarrow$ هر دو عبارت الف و د صحیح است و گزینه 2 صحیح است.
$\eqalign{ & ({b_{15}} - {1 \over 4}) \times M \times {2^s} \cr & S = \sum\limits_{i = 10}^{14} {{b_i}{{( - 2)}^{i - 10}}\,,\,M = } \sum\limits_{i = 0}^9 {{b_i}{{( - {1 \over 2})}^{10 - i}}} \cr} $
کوچکترین و بزرگترین عدد قابل نمایش در این سیستم به ترتیب برابرند با:
$\sum^{\mathrm{9}}_{\mathrm{i=0}}{{\mathrm{b}}_i{\mathrm{(-}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{)}}^{\mathrm{10-i}}\mathrm{=}{\mathrm{b}}_0{\mathrm{2}}^{\mathrm{-}\mathrm{10}}\mathrm{-}}{\mathrm{b}}_{\mathrm{1}}{\mathrm{2}}^{\mathrm{-}\mathrm{9}}\mathrm{+}{\mathrm{b}}_{\mathrm{2}}{\mathrm{2}}^{\mathrm{-}\mathrm{8}}\mathrm{-}{\mathrm{b}}_{\mathrm{3}}{\mathrm{2}}^{\mathrm{-}\mathrm{7}}\mathrm{+......-}{\mathrm{b}}_{\mathrm{9}}{\mathrm{2}}^{\mathrm{-}\mathrm{1}}$
Mبزرگترین مقدار مثبت ${\mathrm{M}}_{\mathrm{+}}\mathrm{=}{\mathrm{2}}^{\mathrm{-}\mathrm{10}}\mathrm{+}{\mathrm{2}}^{\mathrm{-}\mathrm{8}}\mathrm{+}{\mathrm{2}}^{\mathrm{-}\mathrm{6}}\mathrm{+.....+}{\mathrm{2}}^{\mathrm{-}\mathrm{2}}$
Mبزرگترین مقدار منفی ${\mathrm{M}}_{\mathrm{-}}\mathrm{=}{\mathrm{2}}^{\mathrm{-}\mathrm{9}}\mathrm{-}{\mathrm{2}}^{\mathrm{-}\mathrm{7}}\mathrm{-}{\mathrm{2}}^{\mathrm{-}\mathrm{5}}\mathrm{-}\mathrm{.....-}{\mathrm{2}}^{\mathrm{-}\mathrm{1}}$ $S=\sum^{14}_{i=10}{b_i{(-2)}^{i-10}=b_{10}{(-2)}^0+b_{11}{(-2)}^1+b_{12}{(-2)}^2+...+b_{14}{(-2)}^4}$ sبزرگترین مقدار مثبت $= S_+=2^0+2^2+2^4=1+4+16=21$
ما کوچکترین عدد منفی و بزرگترین مثبت را می خواهیم پس با حالت بندی روی $b_{15}$ و $M_+$ و $M_-$ کران ها را در می آوریم.
$\Leftarrow$ گزینه 4 صحیح است.
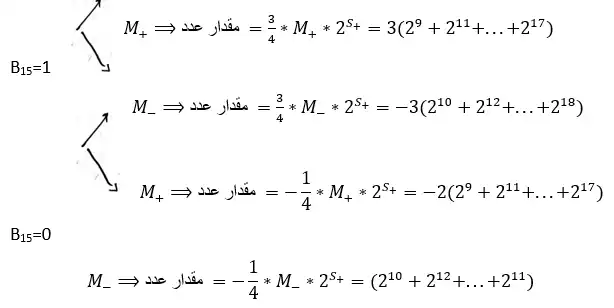
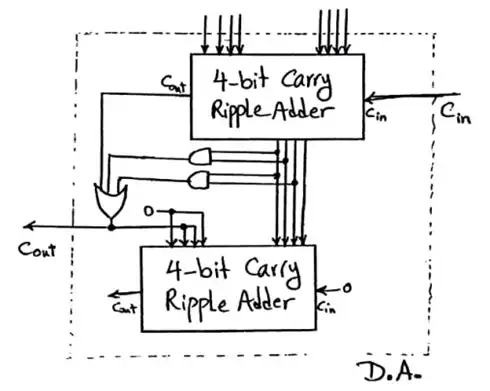
می دانیم مدار کشیده طبق صورت سوال همان BCD-Adder است و برای این مدار همچنین بلد هستیم که تاخیر n رقم دهدهی که توسط این مدار جمع آنها محاسبه می شود برابر $10*(n-1)t+16t$
$\left\{ \begin{array}{c} n=10 \\ \mathrm{t=}t_{gate}=2ns \end{array} \right.$ مجموع تاخیر و $=10*9*2+16*2=212ns$
$\Leftarrow $ گزینه 1 صحیح است.
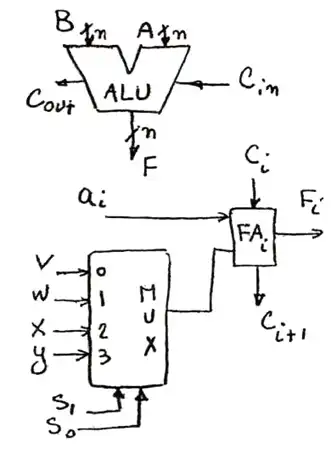
در حالتی که $C_{in} , S_1 , S_0$ هر 3 برابر 0 هستند خروجی تابع F برابر A هست $\Leftarrow$
خروجی mux باید برابر صفر باشد و چون در حالت $00=S_1\ S_0$ خط ورودی V انتخاب می شود در نتیجه $V=0$ باید باشد.
در حالتی که $S_1 , S_0 =01$ و $C_{in}=1$ است خروجی F برابر A-B است که برابر $A+\overline{B}+1$ است در نتیجه خروجی mux باید $\overline{B}$ باشد و چون $S_1 , S_0=01$ است، خط ورودی w انتخاب می شود در نتیجه $w= \overline{b_i}$ باشد.
$\Leftarrow$ با بررسی همین در حالت گزینه های 1و3و4 رد می شود و گزینه 2 پاسخ خواهد بود.
| 11 | 4 | 1 |
وقتی اعداد کوچک هستند، فاصله بین آنها کم است و وقتی اعداد بزرگ باشند فاصله بین هر دو عدد نیز بزرگ است. لذا فاصله بین (کوچکترین دو عدد مثبت) و فاصله بین (بزرگترین دو عدد مثبت) را محاسبه می‌کنیم.
لذا محدوده‌ی تغییرات دقت بدست می‌آید:
$\left\{ \begin{array}{c} \emptyset .\circ \circ \circ \circ \circ \circ \circ \circ \circ \circ \mathrm{1}\times {\mathrm{2}}^{-\mathrm{8}}={\mathrm{2}}^{-\mathrm{11}}\times {\mathrm{2}}^{-\mathrm{8}}={\mathrm{2}}^{-\mathrm{19}} \\ \emptyset .\circ \circ \circ \circ \circ \circ \circ \circ \circ \mathrm{1}\circ \times {\mathrm{2}}^{-\mathrm{8}}={\mathrm{2}}^{-\mathrm{10}}\times {\mathrm{2}}^{-\mathrm{8}}={\mathrm{2}}^{-\mathrm{18}} \end{array} {{\stackrel{\ \ \ \ \ -\ \ \ \ \ \ }{\longrightarrow}}}{\mathrm{2}}^{-\mathrm{19}}\text{اختلاف}\mathrm{\ }\text{این}\mathrm{\ }\text{دو}\right.$دو عدد مثبت کوچک متوالی
$\left\{ \begin{array}{c} \emptyset .\mathrm{11111111111}\times {\mathrm{2}}^{\mathrm{7}} \\ \emptyset .\mathrm{111111111}\circ \mathrm{1}\times {\mathrm{2}}^{\mathrm{7}} \end{array} {{\stackrel{\ \ \ \ \ -\ \ \ \ \ \ }{\longrightarrow}}}{\mathrm{2}}^{-\mathrm{4}}\text{اختلاف}\mathrm{\ }\text{این}\mathrm{\ }\text{دو}\right.$دو عدد مثبت بزرگ متوالی
$\underbrace{a_{\mathrm{2}n-\mathrm{1}}a_{\mathrm{2}n-\mathrm{c}}}_{\text{بیت}\mathrm{\ }\text{بالا}\mathrm{\ }n}......a_{\mathrm{2}}a_{\mathrm{1}}a_{\mathrm{\circ }}|\underline{b_{n-\mathrm{1}}b_{n-\mathrm{c}}....b_{\mathrm{1}}b_{\mathrm{\circ }}}$
اگر n بیت بالای مقسوم عددی بزرگتر یا مساوی مقسوم‌عليه باشد سرریز رخ می‌دهد.
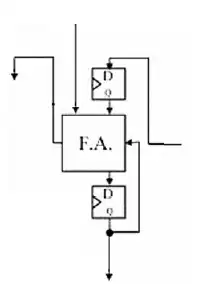
با خروجی 15 بیتی می‌توان حاصل جمع 257 عدد 8 بیتی را محاسبه کرد که با توجه به اینکه مدار Carry-Save Adder ترتیبی مانند خط لوله عمل می‌کند، این محاسبه در زمان 265 = 1 - 8 + 258 کلاک صورت می‌گیرد.
نمونه سوالات RTL درس معماری کامپیوتر
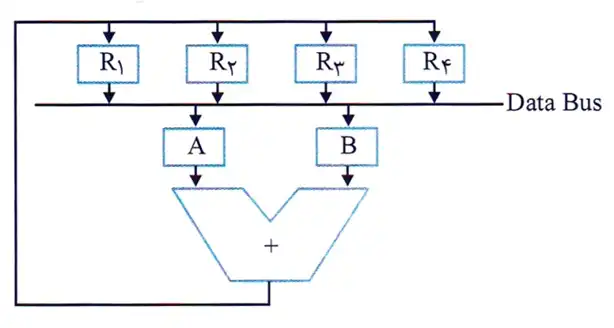
1 - مراحل اجرای دستور $R_1\longleftarrow R_1\ +\ R_2$:
$1)~A\longleftarrow R_1$
$2)~B\longleftarrow\ R_2$
$3)~R_1\longleftarrow A\ +\ B$
2 – مراحل اجرای دستور $R_1\longleftarrow R_1\ +\ R_2$:
$1)~A\longleftarrow R_3$
$2)~B\longleftarrow\ R_4$
$3)~R_1\longleftarrow A\ +\ B$
همانطور که مشاهده کردیم، هر یک از دستورات بالا در 3 پالس ساعت انجام می‌شوند.
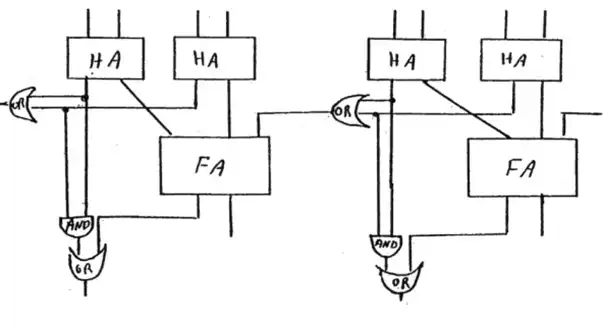
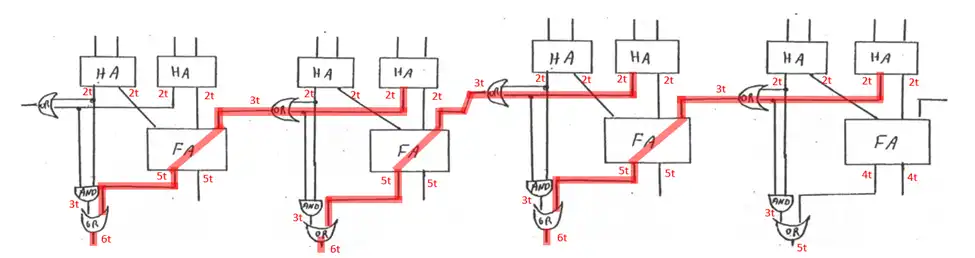
به منظور درک بهتر، آنچه را که سوال گفته است در شکل بالا رسم کردیم (جلوتر می‌گوییم که لزومی ندارد شکل آن را دقیقا رسم کنید!) در شکل بالا مسیرهای بحرانی از ورودی تا خروجی با توجه به تاخیر گیت‌ها مشخص شده‌اند. (چون در صورت سوال اشاره به تاخیر گیت نشده، آن را برابر $t$ در نظر می‌گیریم) مشخص است که هر تعداد سلول اگر کنار هم باشند، خروجی طبقه اول مدار پس از $2t$ آماده می‌شود. همچنین چون ورودی‌های گیت $OR$ در هر سلول، فارغ از طبقات قبل پس از $2t$ آماده می‌شوند در نتیجه پس از تاخیر $3t$ (تاخیر گیت $OR$) خروجی گیت $OR$ کلیه سلول‌ها نیز آماده می‌شود. پس از زمان $3t$ همه ورودی‌های $FA$ هر سلول فارغ از وابستگی به کلیه‌ی طبقات قبل، آماده می‌شود. در نهایت چون ورودی گیت‌های $OR$ طبقه آخر هر سلول پس از $5t$ آماده شده، خروجی هر سلول پس از $6t$ آماده است. در نتیجه اضافه کردن هر تعداد سلول در تاخیر مسیر بحرانی تاثیری ایجاد نمی‌کند.
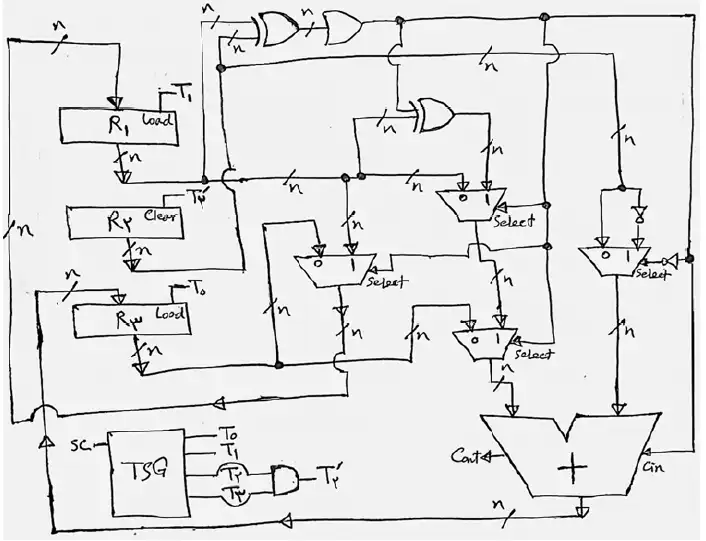
با توجه به این که سیگنال‌های کنترلی انتخاب مالتی‌پلکسرها رقم نفلی جمع‌کننده با مساوی نبودن محتوای ثبات‌های $R_{\mathrm{1}}$ و $R_{\mathrm{2}}$ برابر یک می‌شود، خواهیم داشت:
$T_{\mathrm{\circ }}\mathrm{:}if\left(R_{\mathrm{1}}\mathrm{=}R_{\mathrm{2}}\right)then\mathrm{\ }R_{\mathrm{3}}\mathrm{\leftarrow }{\overline{R}}_{\mathrm{2}}\mathrm{-}R_{\mathrm{3}}\mathrm{=}R_{\mathrm{3}}\mathrm{-}R_{\mathrm{2}}\mathrm{-}\mathrm{1}$
${else\mathrm{\ }R}_{\mathrm{3}}\mathrm{\leftarrow }{\overline{R}}_{\mathrm{1}}\mathrm{+}R_{\mathrm{2}}\mathrm{+}\mathrm{1}\mathrm{=}R_{\mathrm{2}}\mathrm{-}R_{\mathrm{1}}$
$T_{\mathrm{1}}\mathrm{:}if\left(R\mathrm{1}\mathrm{\neq }R\mathrm{2}\right)then\mathrm{\ }R_{\mathrm{1}}\mathrm{\leftarrow }{\overline{R}}_{\mathrm{1}}\mathrm{+}R_{\mathrm{2}}\mathrm{+}\mathrm{1}\mathrm{=}R_{\mathrm{2}}\mathrm{-}R_{\mathrm{1}}$
${else\mathrm{\ }R_{\mathrm{1}}\mathrm{\leftarrow }R}_{\mathrm{3}}$
$T_{\mathrm{2}}{\mathrm{\vee }T}_{\mathrm{3}}\mathrm{:}\mathrm{\emptyset }$
$idle:idle\leftarrow \circ _{} ,_{} enable\leftarrow \circ _{} ,_{} A\leftarrow 1_{} ,_{} B\leftarrow \circ $
$A\mathrm{:}A\leftarrow \circ \ \mathrm{,\ \ }if\mathrm{(}x \lt y\mathrm{)}then\mathrm{(}enable\leftarrow \mathrm{1)}elseB\leftarrow \mathrm{1}$
$B:x\leftarrow x-y_{} ,_{} A\leftarrow 1_{} ,_{} B\leftarrow \circ $
در واقع بعد از حالت شروع idle، ابتدا باید چک کنیم که آیا x از y کوچکتر هست که در این صورت پاسخ همان x است و نیازی به اجرای سطر سوم نیست (به همین دلیل 3 و 4 غلط هستند). از طرفی ما باید هر بار $x \lt y$ را چک کنیم که اگر برقرار نبود x-y را در x قرار دهیم و دوباره چک کنیم.
نمونه سوالات طراحی کامپیوتر درس معماری کامپیوتر
A. در معماری RISC امکان آدرس‌دهی غیرمستقیم در حافظه وجود ندارد.
B. در معماری CISC آدرس دستور بعدی همزمان با واکشی دستور فعلی قابل انجام است.
C. در معماری RISC تغییرات در واحد کنترل انعطاف‌پذیری کمتری دارد.
چون در CISC طول دستورات متغیر است لذا امکان محاسبه آدرس دستور بعدی به‌طور همزمان با واکشی دستور فعلی وجود ندارد. حافظه کنترل در معماری RISC وجود دارد و باعث انعطاف‌پذیری در تغییرات شده است.
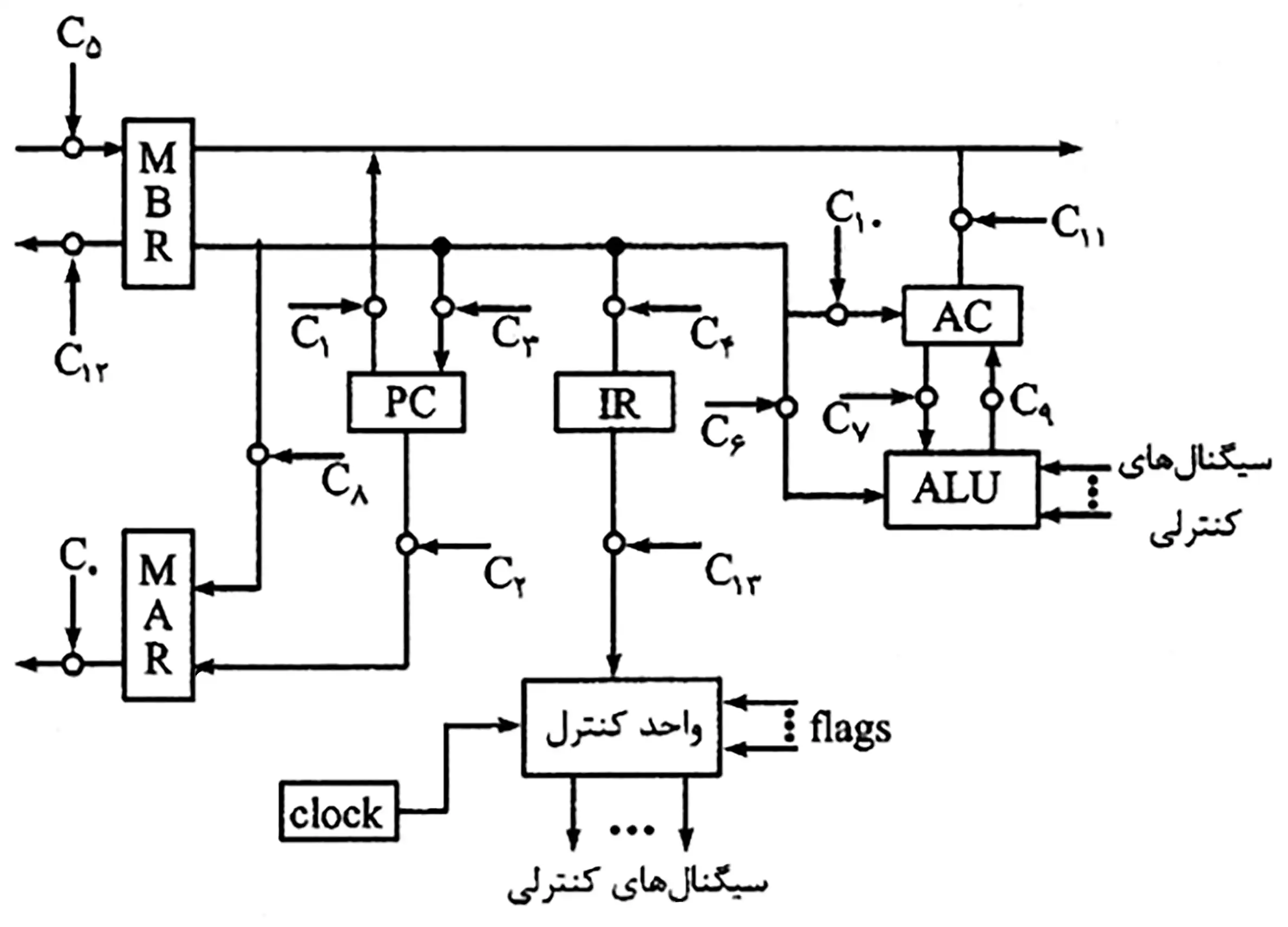
$Fetch:$
$t_\mathrm{1}:MAR\gets pc$ $t_\mathrm{2}:MBR\gets Memoty,~pc\gets pc+\mathrm{1}$ $t_\mathrm{3}:IR\gets MBR$ $C_\mathrm{2}\rightarrow C_\mathrm{\circ}\rightarrow C_\mathrm{5}\rightarrow C_\mathrm{4}$
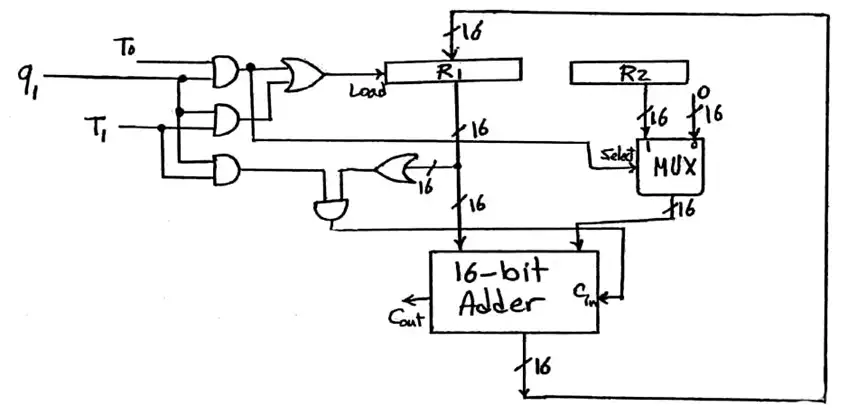
گزینه 3 صحیح است.
این سوال را در 2 حالت حل می کنیم.
حالت 1) $Q_0=1\ \ T_0=1 \Leftarrow T_0Q_1=1$ (با رنگ قرمز نشان می دهیم.)
و همچنین (چون $T_0$ و $T_1$ سیگنال زمانی هستند و باهم نمی تواند 1 شوند.)
$\Rightarrow T_0Q_1=R_1 \leftarrow R_1+R_2$
حالت 2) $T_0=0 \ \ Q_1=1 \ \ T_1=1 \Leftarrow T_0Q_1=1$ (با رنگ سبز نشان می دهیم.)
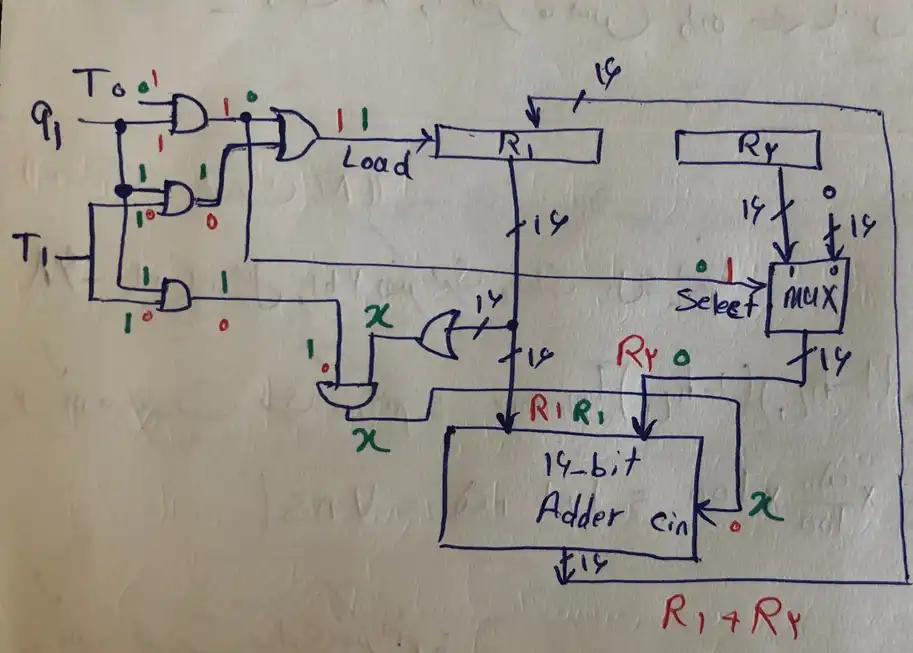
$If\ R_1=0\to X=0\to Cin=0$
$If \ R_1\neq 0\to X=Cin=1$
$\Rightarrow T_1Q_1:if\ (R_1\neq 0)$ then ${(R}_1\leftarrow R_1+1)$ else ${(R}_1\leftarrow R_1)$
$\Leftarrow$ گزینه 3 صحیح است.
گزینه 2 صحیح است.
چون طول ثبات IR شانزده بیت است $\leftarrow$ طول قالب و دستورات را 16 بیت در نظر می گیریم.
چون طول ثبات ACC را به صورت سوال به ما داده است $\leftarrow$ اندازه Data ها برابر 8 بیت به اندازه ثبات ACC است.
و همچنین چون طول MAR 10 بیت است $\leftarrow$ آدرس را 10 بیتی در نظر می گیریم.
و همچنین چون ما در شیوه نشان دهی مستقیم و بلافاصله داریم $\leftarrow$ بیت نوع در نظر می گیریم.
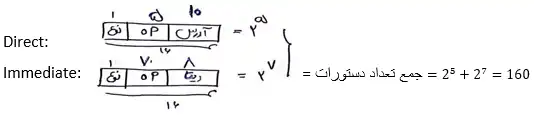
$\Leftarrow$ گزینه 2 صحیح است.
B = ۰۱۰۱۱۰۱۰
A = ۱۰۱۰۰۱۰۱
(در لحظه شروع، عدد ۸ بیتی A در مکان ۸ بیت کم ارزش رجیستر۱۶ بیتی p قرار می‌گیرد.)
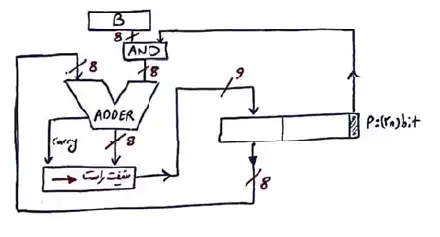
ابتدا بیت سمت راست A را نگاه می‌کنیم، چون 1 هست B را با 0 جمع می‌کنیم و حاصل را در قسمت با ارزش p قرار می‌دهیم، بنابراین در این لحظه حاصل ثبات p بصورت زیر است:
P=0101101010100101
حال باید ثبات p را به سمت راست شیفت دهیم، چون کری جمع B با 0 برابر 0 است، از سمت چپ صفر وارد می‌کنیم، بنابراین بعد از سیکل اول مقدار درون ثبات P بصورت زیر خواهد بود
0010110101010010=p بعد از سیکل اول
با توجه به 0 بودن کم ارزش ترین بیت P درسیکل دوم فقط کافی است P را به سمت راست شیفت دهیم:
0001011010101001=p بعد از سیکل دوم
بنابراین مقدار 8 بیت کم ارزش بیت P در انتهای سیکل دوم برابر است با:
$\mathrm{1}\mathrm{\circ }\mathrm{1}\mathrm{\circ }\mathrm{1}\mathrm{\circ }\mathrm{\circ }\mathrm{1}\mathrm{=}\mathrm{169}\mathrm{\ }$
• قالب دستورات سه عملوندی شامل فیلدهای $\boxed{\mathrm{opc}\ |\ \mathrm{dest}\ |\ {\mathrm{src}}_{\mathrm{1}}\ |\ {\mathrm{src}\mathrm{\ }}_{\mathrm{2}}}$ می‌باشد.
• قالب دستورات تک عملوندی شامل فلیدهای $\boxed{\mathrm{\ \ \ \ \ \ \ \ \ \ \ opc}\ \ \ \ \ \ \ \ \ \ |\ \mathrm{opr}\ }$ می‌باشد.
• قالب دستورات صفر عملوندی فقط شامل فیلد $\boxed{\mathrm{\ \ \ \ \ \ \ \ \ \ \ \ \ opc}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }$ می‌باشد.
برای اینکه پردازنده ما بیشترین تعداد دستورات را داشته باشد، باید 1 دستور ماشین را به قالب دستورات 3 عملوندی و همین طور 1 دستور را به قالب دستورات تک عملوندی نسبت دهیم و سایر دستورات را بدون عملوند در نظر بگیریم. برای محاسبه پاسخ ابتدا کل دستورات 3 فیلد آدرسی را محاسبه می‌کنیم ($2^n$) ، سپس یک دستور را به دستورات 3 فیلد آدرسی اختصاص می‌دهیم و بقیه حالت‌های باقیمانده را برای دستورات تک فیلد آدرسی نگه می‌داریم ($2^n-1$). سپس تعداد کل دستورات تک فیلد آدرسی که می‌توانیم داشته باشیم را بدست می‌آوریم ($\left(2^n-1\right)\times2^{2n}$) و سپس یک دستور را به دستورات تک فیلد آدرسی اختصاص می‌دهیم و بقیه حالت‌های باقیمانده را برای دستورات بدون فیلد آدرس نگه می‌داریم ($\left(2^n-1\right)\times2^{2n}-1$)
\[\underbrace{\left(\overbrace{\left(2^n-1\right)}^{\text{یک}\mathrm{\ }\text{دستور}\mathrm{\ }\text{برای}\mathrm{\ }\text{اولی}}\times 2^{2n}-1\right)}_{\text{یک}\mathrm{\ }\text{دستور}\mathrm{\ }\text{برای}\mathrm{\ }\text{دومی}}2^n+\overbrace{1}^{\text{تک}\mathrm{\ }\text{دستور}\mathrm{\ 3\ }\text{عملوندی}}+\overbrace{1}^{\text{یک}\mathrm{\ }\text{دستور}\mathrm{\ }\text{تک}\mathrm{\ }\text{عملوندی}}=\left(2^{3n}-2^{2n}-1\right)\times 2^n+2=2^{4n}-2^{3n}-2^n+2\]
برای ساخت یک گذرگاه مشترک بدون سیگنال‌های load، مساحت سخت‌افزار گذرگاه، در حالتی که ۲۰ ثبات ۳ بیتی را به هم وصل می‌کند چند برابر مساحت سخت‌افزار گذرگاه در حالتی است که ۶ ثبات ۶ بیتی را به هم وصل خواهد کرد؟ طراحی کامپیوتر
وقتی سیگنال‌های load را برای گذرگاه مشترک در نظر نمی‌گیریم، نیازی به دیکودر نیست.
برای ساخت گذرگاه مشترک که تعداد $(2^{K-1} \lt x\le 2^{K} )$ تا ثبات L بیتی را به هم وصل می‌کند، به تعداد L تا Mux با $2^{K} $ ورودی (با K سیگنال انتخاب) نیاز هست. (دقت کنید که ورودی مالتی پلکسر باید توانی از 2 باشد)
$\Rightarrow S_{1} =3\left[2(32)+2\right]=3(66)$ 3 تا Mux = (هر کدام 32 ورودی) نیاز هست
$\Rightarrow S_{2} =6\left[2(8)+2\right]=6(18)$ 6 تا Mux = (هر کدام 8 ورودی) نیاز هست
$\frac{S_{1} }{S_{2} } =\frac{3(66)}{6(18)} =\frac{11}{6} =1/83$
نمونه سوالات ارزیابی کارایی درس معماری کامپیوتر
0.2n از دستورات $\Leftarrow$ ضرب (0.2t)
0.4n از دستورات $\Leftarrow$ جمع (0.4t)
0.2n از دستورات $\Leftarrow$ ارجاع به حافظه (0.2t)
0.2n از دستورات $\Leftarrow$ باقی دستورات (0.2t)
t: زمان کل
بررسی گزینه 1: $t_{new}=\frac{0.2t}{4}+\frac{0.2t}{4}+0.6t=0.7t$ بررسی گزینه 2: $t_{new}=\frac{0.2t+0.4t}{3}+0.4t=0.6t$ بررسی گزینه 3: $t_{new}=\frac{0.2t}{20}+0.8t=0.81t$ بررسی گزینه 4: $t_{new}=\frac{0.4t}{5}+0.6t=0.68t$
پیشنهاد اول: تابع ریشه دوم را ده برابر سریع می‌کنیم.
پیشنهاد دوم: همه دستورهای floating point را 2 برابر سریعتر می‌کنیم. این عملیات اعشاری 50 درصد زمان آن کار گرافیکی را اشغال می‌کند. کدام‌یک از این دو پیشنهاد برای اجرای آن کار گرافیکی سریعتر می‌باشد. ارزیابی کارایی
گزینه 2 صحیح است.
اگر فرض کنیم کل زمان اجرای کارهای گرافیکی برابر 10T باشد. طبق صورت سوال 2T مربوط به اجرای تابع ریشه دوم است و 5T مربوط به اجرای دستورات floating point و 3T باقی کارها.
حال هر پیشنهاد و زمان هریک را محاسبه می کنیم.
پیشنهاد 2 زمان اجرا را بیشتر کاهش داده $\leftarrow$ ماشین دوم سریع تر است $\Leftarrow$ گزینه 2 صحیح است.
ماشین A: تمامی دستورات پردازش سیگنال را (۲) برابر سریعتر کنیم.
ماشین B: اجرای عملیات MAC را تا حد ممکن سریعتر کنیم. ارزیابی کارایی
قانون امدال:
${\ speedup}_{\left(A\right)}:\frac{\mathrm{1}}{(\mathrm{1-0/4})+\frac{\mathrm{0/4}}{\mathrm{2}}}=\mathrm{1/25}$ :ماشین A
نکته: درصد مربوط به MAC در بین کل دستورات پردازنده همه منظوره:
$\mathrm{=\ }\frac{\mathrm{40}}{\mathrm{100}}\times \frac{\mathrm{50}}{\mathrm{100}}=\frac{\mathrm{20}}{\mathrm{100}}$ : درصد MAC
${\ speedup}_{\left(B\right)}:\frac{\mathrm{1}}{(\mathrm{1-0/2})+\frac{\mathrm{0/2}}{\mathrm{n}}}=\frac{\mathrm{1}}{\frac{\mathrm{8}}{\mathrm{10}}+\frac{(\frac{2}{n})}{\mathrm{10}}}\mathrm{=}\frac{\mathrm{10}}{\mathrm{8+}\frac{2}{n}}\mathrm{ \lt }\mathrm{1/25}$ : ماشین B
CPI متوسط دستورات محاسباتی به صورت بدست می‌آید.
${cpI}_{old}\mathrm{=}\mathrm{0/4}\mathrm{\times }\mathrm{1}\mathrm{+}\mathrm{0/3}\mathrm{\times }\mathrm{5}\mathrm{+}\mathrm{0/3}\mathrm{\times }\mathrm{2}\mathrm{=}\mathrm{2/5}$
${cpI}_{old}\mathrm{=}\mathrm{0/4}\mathrm{\times }\mathrm{1}\mathrm{+}\mathrm{0/3}\mathrm{\times }\mathrm{3}\mathrm{+}\mathrm{0/3}\mathrm{\times }\mathrm{2}\mathrm{=}\mathrm{1/9}$
$speedup=\frac{{cpI}_{old}\mathrm{\times }\mathrm{0/82}\mathrm{+}{cpI}_{IO}\mathrm{\times }\mathrm{0/18}}{{cpI}_{new}\mathrm{\times }\mathrm{0/82}\mathrm{+}{cpI}_{IO}\mathrm{\times }\mathrm{0/18}}=\frac{\mathrm{2/41}}{\mathrm{1/918}}=\mathrm{1/245}$
نمونه سوالات موازات و پایپلاین درس معماری کامپیوتر
$\frac{\mathrm{1}}{{\mathrm{10}}^{\mathrm{9}}HZ}=\mathrm{1}ns$=دوره تناوب جمع کننده‌ی خط لوله‌ایی
$\frac{\mathrm{1}}{200\times {\mathrm{10}}^{\mathrm{6}}HZ}=\mathrm{5}ns$= دوره تناوب جمع کننده‌ی تمام ترکیبی
جمع کننده‌ی خط لوله در هر 9 کلاک دو عدد 64 بیتی را جمع می‌کند به عبارت دیگر ما پایپلاینی داریم با 9 stage مدت زمان اجرای 32 دستور در یک پایپلاین با 9 مرحله و دوره تناوب ns 1 برابر است با:
$(9+31)\times 1ns=40 ns$
(برای فهم بهتر فرض می‌کنیم دستور اول کل پایپلاین را طی می‌کند و به 9 کلاک نیاز دارد و 31 دستور بعدی هر کدام با 1 کلاک اجرا می‌شوند.)
زمان اجرا با جمع کننده ترکیبی برابر است با:
$32\times 5=160\ ns$
همانطور که مشخص است جمع کننده‌ی خط لوله‌ایی، 4 برابر سریعتر عمل می‌کند.
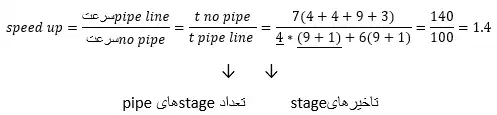
$\Leftarrow $ گزینه 1 صحیح است.
ابتدا زمان اجرای $n$ دستور در پايپلاين $3$ سطحی را محاسبه می‌کنيم. می‌دانيم که هر $p$ دستور پرش (اگر دستور آخر پرش نباشد) تشکيل $p + 1$ دسته داده و هر دسته ما را $k – 1$ ($k$ تعداد سطوح پايپلاين) کلاک جريمه می‌کند. پس داريم:
$\left(n+3-1\right)\times T+0/3n\times2\times T=1/6nT+2T$
محاسبه زمان اجرای n دستور در پايپلاين 4 سطحی:
$(n\ +\ 4\ -\ 1)\times0/9T\ +\ 0/3n\times3\times0/9T\ =\ 1/71nT\ +\ 2/7T$
$\frac{t_1}{t_2}\ =\ \frac{1/6nT+2T}{1/71nT\ +\ 2/7T}$
| 11 | 8 | 7 | 10 | 4 |
| fetch | Decode | exe | mem | WB |
| $\mathrm{\sqrt{}}$ | $\mathrm{\sqrt{}}$ | $\mathrm{\sqrt{}}$ | $\mathrm{\sqrt{}}$ | $\mathrm{\sqrt{}}$ |
| $\mathrm{\sqrt{}}$ | $\mathrm{\sqrt{}}$ | $\mathrm{\sqrt{}}$ | ― | $\mathrm{\sqrt{}}$ |
| دستورات حافظه | 80% |
| دستورات بدون نیاز به حافظه | 20% |
$speed\ up=\frac{Performance(pipe)}{Performance(without\ pipe)}=\frac{T(without\ pipe)}{T(\ pipe)}$ $=\frac{(\frac{\mathrm{8}}{\mathrm{10}}n)(\mathrm{11}+\mathrm{8}+\mathrm{7}+\mathrm{1}0+\mathrm{4})+(\frac{\mathrm{2}}{\mathrm{10}}n)(\mathrm{11}+\mathrm{8}+\mathrm{7}+\mathrm{4})}{(طبقه)\ \mathrm{5}(\mathrm{11}+\mathrm{1})+(\mathrm{n}\mathrm{-}\mathrm{1})\mathrm{(}\mathrm{11}+\mathrm{1})}$
$=\frac{\mathrm{38}\mathrm{n}}{\mathrm{12}\mathrm{n}\mathrm{+48}}>\mathrm{1}\Rightarrow \mathrm{38}\mathrm{n>}\mathrm{12}\mathrm{n+}\mathrm{48}$ (به ازای $n > 1$ برقرار است)
25 = 5 + 5 + 9 + 3 + 3 = زمان اجرای هر دستور در حالت بدون خط لوله
(ns) 10 × 25 = 250 = زمان اجرای ده تا دستور در حالت بدون خط لوله
10 = 1 + 9 = 1 + { 5, 5, 9, 3, 3} Max = زمان هر مرحله خط لوله
140= 10 × (1 – 10 + 5) =هر مرحله خط لوله ${=(K+n-\mathrm{1})}^*T$ زمان اجرای10 دستور در حالت خط لوله
$\mathrm{=}\frac{\mathrm{250}}{\mathrm{140}}\simeq \mathrm{1/78}$ $\frac{\text{زمان}\boldsymbol{\mathrm{\ }}\text{اجرای}\boldsymbol{\mathrm{\ }}\text{بدون}\boldsymbol{\mathrm{\ }}\text{خط}}{\text{زمان}\boldsymbol{\mathrm{\ }}\text{اجرای}\boldsymbol{\mathrm{\ }}\text{خط}}$ $=$ افزایش سرعت
نمونه سوالات حافظه ها درس معماری کامپیوتر
${\mathrm{2}}^{\mathrm{32}}B=\mathrm{4}GB$ = حجم حافظه = آدرس 32 بیتی
$\mathrm{8}KB={\mathrm{2}}^{\mathrm{13}}B={\mathrm{2}}^{\mathrm{13}}\times {\mathrm{2}}^{\mathrm{3}}bit={\mathrm{2}}^{\mathrm{16}}bit=\mathrm{65536}bit$ = ظرفیت دیتا کش
$\mathrm{64}B$ = اندازه بلاک
هر بلاک یک بیت برای valid، یک بیت برای $\text{تعداد}\mathrm{\ }\text{بلاک}\mathrm{\ }\text{کش}=\frac{{\mathrm{2}}^{\mathrm{3}}\times {\mathrm{2}}^{\mathrm{10}}B}{{\mathrm{2}}^{\mathrm{6}}B}={\mathrm{2}}^{\mathrm{7}}\Rightarrow LRU$
و تعدادی بیت برای tag دارد.
$\text{کش}\mathrm{\ }set\ \text{تعداد}=\frac{2^7}{\mathrm{2}}={\mathrm{2}}^{\mathrm{6}}$
$tag\mathrm{\ }\text{اندازه}=log\frac{{\mathrm{2}}^{\mathrm{32}}B}{{\mathrm{2}}^{\mathrm{12}}B}+log\mathrm{2}\mathrm{=}\mathrm{19}\mathrm{+}\mathrm{1}\mathrm{=}\mathrm{20}$
$\underbrace{65536}_{Data}+\underbrace{2^{7} \times 20}_{tag}+\underbrace{2^{7} }_{valid}+\underbrace{2^{7} }_{LRU} $ = تعداد بیت‌های $SRAM$ مورد نیاز
حجم حافظه اصلی $2^{(21+7+4)}=2^{23}B=4*2^{30}B=4GB$ حجم حافظه نهان$2^{(7+4)}=2^{11}B=2*2^{10}B=2KB$
$\Leftarrow$ تا اینجا گزینه های 1 و 2 رد می شوند.
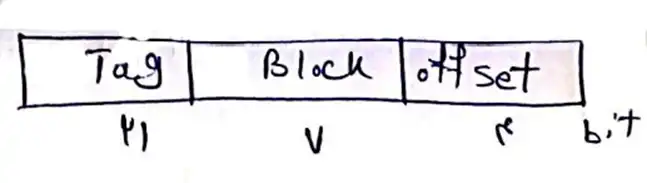
اگر 11 بیت اول (00B3A4F) را بنویسیم به مقدار روبرو می رسیم $(01001001111) \leftarrow$
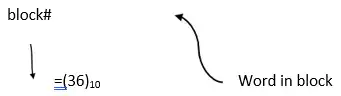
محل استقرار (00B3A4F) در سطر 15 و در Block 36 ام است.
$\Leftarrow$ گزینه 4 صحیح است.
به منظور درک بهتر سوال می‌توان شکل زیر را برای آن در نظر گرفت:
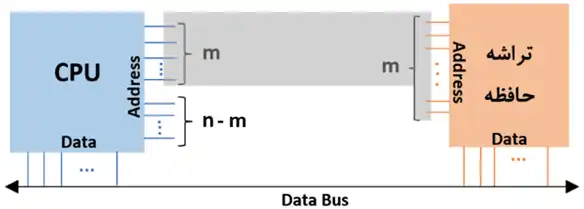
همانطور که از شکل بالا مشخص است، با توجه به فرض سوال چون تعداد خطوط آدرس $CPU$ به اندازه‌ی $n – m$تا از خطوط آدرس تراشه حافظه بیشتر است در نتیجه می‌بایست جهت ارتباط تراشه با $CPU$ کلیه‌ی $m$ خط آدرس تراشه به $m$ خط از خطوط آدرس $CPU$ متصل شود (که با رنگ خاکستری در شکل مشخص شده) $J$ خط داده نیز جهت تبادل $Data$ به یکدیگر متصل شده‌اند. از آنجایی که دستگاه دیگری با توجه به فرض سوال وجود ندارد، $n – m$ خط دیگر آدرس $CPU$ بلااستفاده باقی می‌ماند. اگر $CPU$ نیز تنها دارای $m$ خط آدرس می‌بود، هر کلمه‌ی $J$ بیتی از این تراشه با یک آدرس قابل دسترسی بود اما اکنون به ازای هر آدرس، هر یک از خطوط $n – m$ آدرس دیگر می‌توانند صفر یا یک باشند فارغ از اینکه آدرس آن کلمه تغییر کند(زیرا آن خطوط به جایی متصل نیستند که روی تراشه تاثیر بگذارند). در نتیجه هر کلمه‌ی $J$ بیتی با $2^{n\ -\ m}$ آدرس قابل دسترسی است.
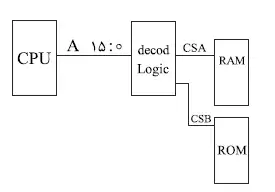
$CSA=\left({\overline{A}}_{\mathrm{15}}+{\overline{A}}_{\mathrm{14}}\right).\left(A_{\mathrm{15}}+A_{\mathrm{14}}+A_{\mathrm{13}}+A_{\mathrm{12}}+A_{\mathrm{11}}+A_{\mathrm{10}}+A_{\mathrm{9}}+A_{\mathrm{8}}\right)$
$CSB=A_{\mathrm{15}}.A_{\mathrm{14}}\left({\overline{A}}_{\mathrm{13}}+{\overline{A}}_{\mathrm{12}}\right)+{\overline{A}}_{\mathrm{15}}.{\overline{A}}_{\mathrm{14}}.{\overline{A}}_{\mathrm{13}}.{\overline{A}}_{\mathrm{12}}.{\overline{A}}_{\mathrm{11}}.{\overline{A}}_{\mathrm{10}}.{\overline{A}}_{\mathrm{9}}.{\overline{A}}_{\mathrm{8}}$
در این صورت چه آدرس‌هایی در RAM و ROM هستند؟
$RAM$ وقتی فعال می‌شود پرانتز اول $CSA$ و دوم آن هر دو یک باشند، ${\overline{A}}_{\mathrm{15}}+{\overline{A}}_{\mathrm{14}}$ برای آدرس‌های ${\mathrm{\circ }\mathrm{\circ }\mathrm{\circ }\mathrm{\circ }}_H$ تا ${\mathrm{BFFF}}_H$ یک است و پرانتز دوم برای آدرس‌های $\mathrm{\circ }\mathrm{1}\mathrm{\circ }\mathrm{\circ }$ تا $\mathrm{\circ }\mathrm{\circ }\mathrm{FF}$ یک است پس $RAM$ شامل آدرس‌های $\mathrm{\circ }\mathrm{1}\mathrm{\circ }\mathrm{\circ }$ تا $\mathrm{BFFF}$ است. $ROM$ شامل $C\circ \circ \circ $ تا $\mathrm{BFFF}$ و $C\circ \circ \circ $ تا $E\mathrm{FFF}$ است.
همه گزینه‌ها صحیح هستند به جز گزینه 4:
زیرا وجود کش در یک سیستم به دلیل spatial locality (محلی بودن مکان) است و نه محلی ترتیبی
$hit\ Rate(cache)=h_{\mathrm{1}}$
برای به صرفه بودن باید:
زمان دستیابی به داده بدون کش > زمان دستیابی به داده با وجود کش
${(h}_{\mathrm{1}})({\mathrm{1}}^{ns})+(\mathrm{1}-h_{\mathrm{1}})(\mathrm{4})({\mathrm{5}}^{ns}) \lt ({\mathrm{5}}^{ns})$ ${\Rightarrow h}_{\mathrm{1}}+\mathrm{20-20}h_{\mathrm{1}} \lt \mathrm{5}$ ${\Rightarrow \mathrm{19}h}_{\mathrm{1}} \gt \mathrm{15}$ ${\Rightarrow h}_{\mathrm{1}}\mathrm{>}\frac{\mathrm{15}}{\mathrm{19}}=\mathrm{0/7894\ =\ \%78/9=\ \%79}$
نمونه سوالات میکرو پروگرامینگ درس معماری کامپیوتر
زبان‌های HDL از کدنویسی همروند پشتیبانی می‌کنند.
سایر گزینه‌ها صحیح هستند.
اندازه ریز حافظه در حالت عادی بدون صرفه جویی
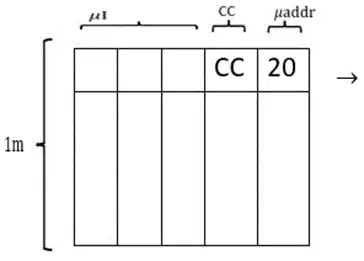
$(200+20+cc)*1m-$
$(cc+18+20)*1m=182m$
میزان صرفه جویی
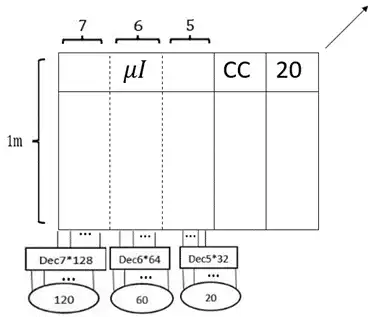
قالب کلی ریز حافظه در حالت پیشرفته به صورت زیر است:
$=1m*(cc+max(200,20))$
اندازه ریز حافظه در حالت پیشرفته با صرفه جویی
$=1m*(cc+max(18,20))$
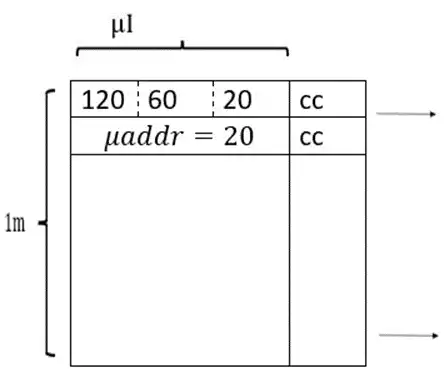
$=1m*(cc=200)-1m*(cc+20)=180m$ میزان صرفه جویی
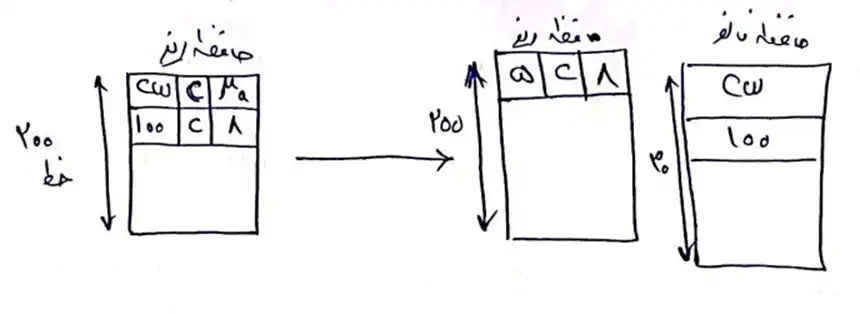
( با استفاده از حافظه نانو ) ( بدون استفاده از حافظه نانو )
$\Leftarrow$ صرفه جویی ریز برنامه
$200*100-200*5=200\left(100+\mathrm{C}+8\right)-200\left(5+\mathrm{C}+8\right)=200*95$
گزینه 1 پاسخ مسئله است.
*نکته: ما در این سوال ها صرفه جویی در حافظه ریز را فقط حساب می کنیم و با حافظه نانو کاری نداریم
مگر اینکه صورت سوال از ما این را بخواهد.
حافظه میکرو (ریزبرنامه) بدون استفاده از نانو: $200 \times 10 = 2000$
حافظه‌ی ریزبرنامه با استفاده از نانو:
(دقت کنید که خود حافظه‌ی نانو را نخواسته است)
از آنجا که 125 جعبه اتصال و 4 جعبه شرطی داریم لذا 129 ریز دستور مختلف مورد نیاز هست که به 8 بیت نیاز دارد و نیز یک بیت هم برای انتخاب نوع جعبه باید در نظر بگیریم. (یعنی 9 بیت)
200=2000-1800 $\Rightarrow $ 1800=9×200= حافظه ریز برنامه و $129 \times 10$= حافظه‌ی نانو
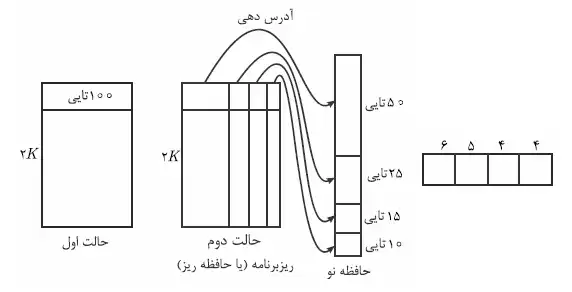
کاهش $(2K)(100)-(2K)(6+5+4+4)=2K(100-19)=(2K)(81)=162K$
نمونه سوالات ورودی و خروجی درس معماری کامپیوتر
کدام گزینه در خصوص این سیستم صحیح است؟ ورودی و خروجی
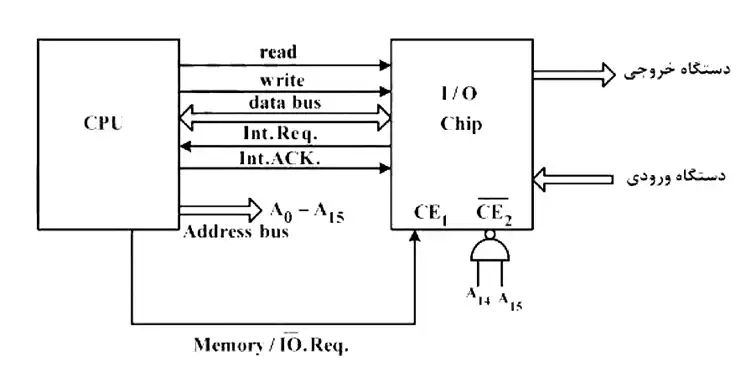
Address bus خارج شده از CPU برای عملیات I/O Programmed از آدرس C000H تا FFFFH قابل دسترس است (رد گزینه ی 4)
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A_{15}\ \ \ A_{14}\ \ \ A_{13}\ \ \ \_\_\_\_\_\_\_\ \ \ \ A_2\ \ \ A_1\ \ \ {\ A}_0$
$\overline{{CE}_2}$ پایه بخاطر $\leftarrow \underline{\overline{\left|1\ \ \ \ \ 1\right|}}\ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \_\_\_\_\_\_\_\ \ \ \ \ 0\ \ \ \ \ 0\ \ \ \ \ \ 0\ \ \ =\ C000H$
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1\ \ \ \ \ 1\ \ \ \ \ 0\ \ \ \ \ \ \ \_\_\_\_\_\_\_\ \ \ \ \ 0\ \ \ \ \ 0\ \ \ \ \ 1\ \ \ =\ C001H$
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;...$
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1\ \ \ \ \ 1\ \ \ \ \ 1\ \ \ \ \ \ \_\_\_\_\_\_\_\ \ \ \ \ 1\ \ \ \ \ 1\ \ \ \ \ 1\ \ \ =\ FFFFH$
همچنین شکل داده شده دارای پایه ی Int.req. است پس می تواند وقفه صادر کند و روش I/O Interrupt ربطی به memory-mapped ندارد (رد گزینه ی 1 و 2)
در این حالت که سوال برای ما کشیده شده است. سیگنال S1 ، Strobe قبل از گذاشتن data روی خط 1 شده است و سپس Data روی باس قرار داده شده است و بعد S2 ، Strobe فعال شده است و پس از اتمام سیگنال S2 , S1 هم تمام شده.
این حالت نشان دهنده حالت گیرنده آغاز کننده است. یعنی S1 گیرنده ما است و سیگنال Strobe آن دست گیرنده و سیگنال S2 ، Strobe دست فرستنده است و در این حالت گیرنده کندتر است و آغاز کننده درخواست است. $\Leftarrow$ گزینه 3 صحیح است.
نمونه سوالات معماری کامپیوتر این صفحه از چه منابعی است؟
در این صفحه از نمونه سوالات معماری کامپیوتر موریس مانو، نمونه سوالات معماری کامپیوتر دانشگاه شریف، نمونه سوالات پایان ترم دانشگاه های برتر کشور، نمونه سوالات معماری کامپیوتر دانشگاه پیام نور، نمونه سوالات معماری کامپیوتر کاردانی علمی کاربردی و دانشگاه آزاد و همین طور سوالات معماری کامپیوتر کنکور ارشد و دکتری رشته های مختلف از جمله کامپیوتر، برق استفاده شده است.
آیا نمونه سوالات معماری کامپیوتر این صفحه جواب دارد و به درد چه کسانی می‌خورد؟
بله. تمامی سوالات معماری کامپیوتر این صفحه با پاسخ های کاملا تشریحی در اختیار شما قرار گرفته است. سوالات این صفحه به درد دانشجویان مقطع لیسانس رشته های مختلف، داوطلبان کنکورهای مقاطع مختلف از جمله ارشد و دکتری، داوطلبان آزمون های استخدامی و افرادی است که به دنبال حل مسائل بیشتر برای مسلط شدن روی معماری کامپیوتر هستند
