برای شروع حرفهای کنکور ارشد کامپیوتر،آیتی و علوم کامپیوتر حتما روی عکس زیر کلیک کنید تا در کانال کنکور کامپیوتر عضو شوید، در این کانال به معرفی بهترین منابع کنکور ارشد،برنامه ریزی و مشاوره، معرفی گرایشها و هر آنچه برای موفقیت در کنکور ارشد نیاز دارید پرداخته شده است

اهمیت یافتن کوتاهترین مسیر
در زندگی روزمره ما، برخورد با مسائلی مانند نیاز به رسیدن به مقصدی با کمترین زمان و منابع، بسیار به چشم میخورد. از جستجوی مسیرهای کوتاه در شبکههای حمل و نقل تا برنامهریزی مسیرهای موثر در سیستمهای اجتماعی، تجاری و فناوری، یافتن کوتاهترین مسیر تاثیر قابل توجهی بر بهبود کارایی و بهرهوری دارد.
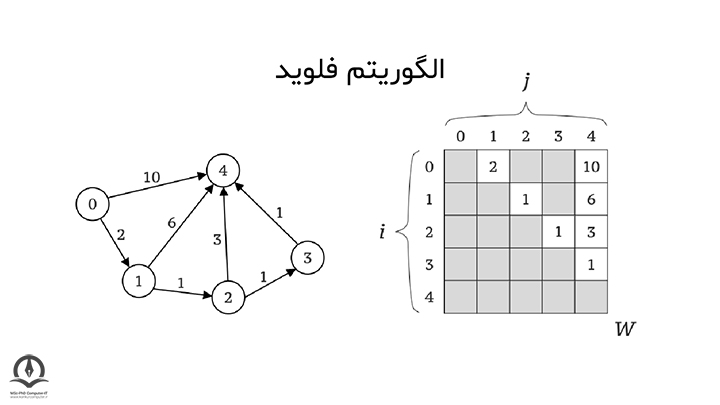
معرفی الگوریتم فلوید و کاربردهای آن
الگوریتمالگوریتم چیست به زبان ساده و با مثال های فراوان در این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد فلوید یک الگوریتم برنامه نویسی پویابرنامه نویسی پویا چیست، برنامه نویسی پویا در طراحی الگوریتم
در این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد فلوید یک الگوریتم برنامه نویسی پویابرنامه نویسی پویا چیست، برنامه نویسی پویا در طراحی الگوریتم این صفحه عالی به معرفی برنامه نویسی پویا یا Dynamic programming پرداخته و کاربردها و مثال هایی از برنامه نویسی پویا در طراحی الگوریتم آورده است
است که برای یافتن کوتاه ترین مسیرها بین همه جفت نقاط در یک گرافگراف چیست، آموزش گراف از 0 تا 100 توسط دانشجو ارشد صنعتی شریف
این صفحه عالی به معرفی برنامه نویسی پویا یا Dynamic programming پرداخته و کاربردها و مثال هایی از برنامه نویسی پویا در طراحی الگوریتم آورده است
است که برای یافتن کوتاه ترین مسیرها بین همه جفت نقاط در یک گرافگراف چیست، آموزش گراف از 0 تا 100 توسط دانشجو ارشد صنعتی شریف در این مقاله تمامی مطالب مربوط به گراف از 0 تا 100 تدریس شده است. مواردی همچون : گراف چیست؟ انواع گراف، گراف همبند، مکمل گراف، گراف کامل، گراف جهت دار، گراف بدون جهت، گراف ساده و ... استفاده میشود. این الگوریتم، با استفاده از یک روش تکراری، مسیرهای کوتاهتر را در گراف پیدا میکند و در نهایت یک ماتریسماتریس در ساختمان داده⚡️معرفی انواع ماتریس (خلوت،قطری)
در این مقاله تمامی مطالب مربوط به گراف از 0 تا 100 تدریس شده است. مواردی همچون : گراف چیست؟ انواع گراف، گراف همبند، مکمل گراف، گراف کامل، گراف جهت دار، گراف بدون جهت، گراف ساده و ... استفاده میشود. این الگوریتم، با استفاده از یک روش تکراری، مسیرهای کوتاهتر را در گراف پیدا میکند و در نهایت یک ماتریسماتریس در ساختمان داده⚡️معرفی انواع ماتریس (خلوت،قطری) این مقاله عالی گفته ماتریس چیست و به آموزش ماتریس پرداخته، همچنین انواع ماتریس از جمله ماتریس خلوت، ماترس قطری و ماتریس های بالا و پایین مثلثی را معرفی کرده
که نشاندهنده کوتاهترین مسیرها است را ساخته و برمیگرداند.
این مقاله عالی گفته ماتریس چیست و به آموزش ماتریس پرداخته، همچنین انواع ماتریس از جمله ماتریس خلوت، ماترس قطری و ماتریس های بالا و پایین مثلثی را معرفی کرده
که نشاندهنده کوتاهترین مسیرها است را ساخته و برمیگرداند.
پیاده سازی مرحله به مرحله الگوریتم فلوید
پیاده سازی مرحله به مرحله الگوریتم فلوید شامل چندین مرحله است. در زیر به صورت خلاصه به پیادهسازی این مراحل اشاره خواهیم کرد:
مرحله مقدماتی: تنظیم ماتریسهای فاصله و مسیر
- ابتدا برای هر جفت نقاط در گراف، فاصله اولیه را تعیین میکنیم.
- سپس ماتریس فاصلهها را بهروزرسانی میکنیم. اگر بین دو نقطه مستقیماً یالی وجود داشته باشد، فاصله برابر طول آن یال قرار میگیرد؛ در غیر این صورت، فاصله بینهایت خواهد بود.
مراحل تکراری: بهروزرسانی ماتریسها برای یافتن مسیرهای کوتاهتر
- در هر مرحله، برای هر جفت نقاط، مسیرهای کوتاهتری که از نقطه مبدأ به نقطه مقصد میروند، بررسی میشوند.
- اگر مسیر مستقیم بین دو نقطه کوتاهتر از مسیر فعلی باشد، مسیر جدید و کوتاهتر جایگزین مسیر قبلی میشود.
- این عملیات تا زمانی ادامه مییابد که همه مسیرهای کوتاهتر برای تمام جفت نقاط محاسبه شوند.
پایان الگوریتم و نتیجه حاصل
- پس از اتمام مراحل تکراری، یک ماتریس نهایی حاوی کوتاهترین مسیرها بین هر جفت نقاط ساخته میشود.
- این ماتریس میتواند بهعنوان یک جدول راهبردی برای یافتن کوتاهترین مسیرها در گراف استفاده شود.
تحلیل پیچیدگی و عملکرد الگوریتم فلوید
تحلیل پیچیدگی و عملکرد الگوریتم فلوید میتواند به ما درکی از کارایی و عملکرد آن در حل مسائل بدهد. در زیر، به تحلیل پیچیدگی زمانیپیچیدگی زمانی الگوریتم چیست؟ معرفی نماد های مجانبی این صفحه عالی به معرفی پیچیدگی زمانی الگوریتم پرداخته، همچنین انواع نماد های مجانبی و پیچیدگی زمانی های برخی از الگوریتم های مرتب سازی و جستجو را توضیح داده
و فضایی الگوریتم فلوید، مزایا و محدودیتهای آن، و مقایسه با سایر الگوریتمها میپردازیم:
این صفحه عالی به معرفی پیچیدگی زمانی الگوریتم پرداخته، همچنین انواع نماد های مجانبی و پیچیدگی زمانی های برخی از الگوریتم های مرتب سازی و جستجو را توضیح داده
و فضایی الگوریتم فلوید، مزایا و محدودیتهای آن، و مقایسه با سایر الگوریتمها میپردازیم:
تحلیل پیچیدگی زمانی و فضایی الگوریتم فلوید
- الگوریتم فلوید در بهترین حالت ممکن، برای محاسبه کوتاهترین مسیرها بین همه جفت نقاط در یک گراف، نیاز به انجام ${\mathrm{n}}^{\mathrm{3}}$ عملیات دارد. ($\mathrm{n}$ نشاندهنده تعداد نقاط است)
- این الگوریتم بهطور کلی با یک شرط ایستا در $\mathrm{n}$ مرحله اجرا میشود و در هر مرحله، بهروزرسانیهایی در ماتریس فاصلهها انجام میدهد.
- بنابراین، پیچیدگی زمانی الگوریتم فلوید برابر $\mathrm{O}\left({\mathrm{n}}^{\mathrm{3}}\right)$ است.
- برای نگهداری ماتریس فاصلهها و ماتریس مسیر، الگوریتم فلوید نیاز به فضای ذخیرهسازی $\mathrm{O}\left({\mathrm{n}}^{\mathrm{2}}\right)$ دارد. ($\mathrm{n}$ نشاندهنده تعداد نقاط است)
- در صورت نیاز به نگهداری ماتریس فاصلهها و مسیر که هر دو ماتریس دارای ابعاد $\mathrm{n}$ در $\mathrm{n}$ هستند، فضای ذخیره سازی برابر $\mathrm{O}\left({\mathrm{n}}^{\mathrm{2}}\right)$ خواهد بود.
مزایا و محدودیتهای الگوریتم فلوید
- مزیت اصلی الگوریتم فلوید این است که بهطور کامل تمام کوتاهترین مسیرها را بین همه جفت نقاط در گراف محاسبه میکند.
- الگوریتم فلوید نیازی به قیدی برای وجود وزنهای مثبت در گراف ندارد و قادر به مدیریت یالهای منفی نیز است.
- محدودیت اصلی الگوریتم فلوید، پیچیدگی زمانی آن است که در حالتهایی که تعداد نقاط بسیار زیاد است، میتواند زمان طولانیتری برای محاسبه نیاز داشته باشد؛ بنابراین، برای گرافهای بزرگتر، الگوریتمهای دیگر مانند الگوریتم دایجستراالگوریتم دایجسترا (Dijkstra) از 0 تا 100 - الگوریتم دایکسترا
 این صفحه الگوریتم دایجسترا (Dijkstra) (یا همان الگوریتم دایکسترا) را از 0 تا 100 بررسی کرده، همین طور به پیاده سازی و آموزش الگوریتم دایجسترا پرداخته است. و *A میتوانند جایگزین مناسبی باشند.
این صفحه الگوریتم دایجسترا (Dijkstra) (یا همان الگوریتم دایکسترا) را از 0 تا 100 بررسی کرده، همین طور به پیاده سازی و آموزش الگوریتم دایجسترا پرداخته است. و *A میتوانند جایگزین مناسبی باشند.
مقایسه الگوریتم فلوید با سایر الگوریتمها
- الگوریتم دایکسترا تنها کوتاهترین مسیر بین یک نقطه مبدأ و سایر نقاط را محاسبه میکند، در حالی که الگوریتم فلوید تمام کوتاهترین مسیرها را بین همه جفت نقاط محاسبه میکند.
- الگوریتم فلوید میتواند در صورت وجود یالهای منفی نیز عمل کند، در حالی که الگوریتم دایکسترا برای گرافهایی که دارای یالهای منفی هستند، صحیح کار نمیکند.
- در صورتی که تعداد نقاط بسیار زیاد باشد، الگوریتم فلوید به دلیل پیچیدگی زمانی بالا، میتواند بهصورت قابل توجهی کند باشد. در این موارد، الگوریتمهای دیگری مانند الگوریتمهای مبتنی بر دایکسترا بهینهتر خواهند بود.
تفاوت الگوریتم فلوید با الگوریتم فلوید وارشال چیست؟
الگوریتمهای فلوید وارشال و فلوید (Floyd-Warshall و Floyd) هر دو برای حل مسائل کوتاهترین مسیر بین گرهها در گرافها استفاده میشوند. این دو الگوریتم بر اساس برنامهریزی دینامیکی کار میکنند و با کمک جدولی به نام جدول فاصله (Distance Table) نتایج خود را ذخیره میکنند. تفاوت اصلی بین الگوریتمهای فلوید وارشال و فلوید در مورد تعداد مراحل محاسباتی است که نیاز دارند و نحوه اجرای خود:
الگوریتم فلوید وارشال
- الگوریتم فلوید وارشالالگوریتم فلوید وارشال چیست، آموزش الگوریتم فلوید وارشال
 الگوریتم فلوید وارشال چیست، این صفحه عالی به بررسی و آموزش الگوریتم فلوید وارشال با مثال پرداخته و نحوه پیاده سازی الگوریتم فلوید وارشال و پیچیدگی آن را گفته
در یک مرحله بیدرنگ تمامی مسیرها بین همهی جفت گرهها را محاسبه میکند؛ به عبارت دیگر، مراحل محاسباتی برای تمامی جفتگرهها بهصورت مستقل اجرا نمیشود، بلکه در یک حلقه واحد اجرا میشوند.
الگوریتم فلوید وارشال چیست، این صفحه عالی به بررسی و آموزش الگوریتم فلوید وارشال با مثال پرداخته و نحوه پیاده سازی الگوریتم فلوید وارشال و پیچیدگی آن را گفته
در یک مرحله بیدرنگ تمامی مسیرها بین همهی جفت گرهها را محاسبه میکند؛ به عبارت دیگر، مراحل محاسباتی برای تمامی جفتگرهها بهصورت مستقل اجرا نمیشود، بلکه در یک حلقه واحد اجرا میشوند. - زمان اجرای الگوریتم فلوید وارشال در گرافهای با تعداد گرههای زیاد، بهطور چشمگیری بیشتر از الگوریتم فلوید است.
- از این الگوریتم برای محاسبه کوتاهترین مسیرها در گرافهای با وزن منفی استفاده میشود.
الگوریتم فلوید
- در مقایسه با الگوریتم فلوید وارشال، الگوریتم فلوید برای محاسبه مسیرها بین جفتگرهها از یک مرحله به مرحله بعدی پیش میرود؛ به عبارت دیگر، محاسبه کوتاهترین مسیر بین هر جفت گره در یک مرحله اجرایی انجام میشود و سپس نتایج در مرحله بعدی استفاده میشوند.
- این الگوریتم از نظر زمانی کارا تر از الگوریتم فلوید وارشال است و در بسیاری از موارد، بهخصوص در گرافهای کوچکتر، عملکرد بهتری از خود نشان میدهد.
- با توجه به روش اجرایی خاص الگوریتم فلوید، بهطور معمول از آن برای مسائلی با وزنهای مثبت استفاده میشود.
تفاوت اصلی بین این دو الگوریتم در تعداد مراحل محاسباتی و عملکرد زمانی آنها است، که در برخی موارد ممکن است منجر به انتخاب یکی از آنها برای حل یک مسئله خاص شود.
کاربردهای عملی الگوریتم فلوید
- الگوریتم فلوید برای برنامهریزی مسیرها در شبکههای حمل و نقل استفاده میشود. با استفاده از این الگوریتم، میتوان مسیرهای کوتاهتر بین نقاط مختلف را تعیین کرده و بهینهسازی زمان سفر، مصرف سوخت و بهرهوری عمومی را ارتقا داد.
- الگوریتم فلوید بهعنوان یک ابزار قدرتمند در تحلیل شبکههای اجتماعی استفاده میشود. با استفاده از این الگوریتم، میتوان مسیرهای کوتاهتر بین افراد یا گروهها را شناسایی کرده و بهعنوان اطلاعاتی برای تحلیل الگوهای رفتاری، شناسایی افراد تأثیرگذار و پیشبینی رفتارهای آینده مورد استفاده قرار داد.
- الگوریتم فلوید در بهینهسازی توزیع منابع نیز کاربرد دارد. با استفاده از این الگوریتم، میتوان مسیرهای کوتاهتر برای ارسال دادهها، توزیع محصولات و بهینهسازی فرآیندهای توزیع را تعیین کرد.
- الگوریتم فلوید بهعنوان یک روش مسیریابی در سیستمهای مبتنی بر شبکه، مانند شبکههای مخابراتی یا شبکههای اینترنت، استفاده میشود. با استفاده از این الگوریتم، میتوان مسیرهای کوتاهتر بین گرهها و دستگاهها را تعیین کرده و بهینهسازی ارتباطات و کاهش هزینهها را ممکن ساخت.
جمعبندی
میتوان گفت الگوریتم فلوید با قابلیت یافتن کوتاهترین مسیرها بین همه جفت نقاط در یک گراف، یکی از الگوریتمهای مهم و کارآمد در حوزه روشهای برنامه نویسی پویا است. این الگوریتم بهعنوان یک ابزار قدرتمند در حل مسائلی که نیاز به یافتن کوتاهترین مسیرها دارند، کاربرد فراوانی دارد. اهمیت یافتن کوتاهترین مسیر در بسیاری از حوزهها نقش مهمی ایفا میکند از جمله شبکههای حمل و نقل، شبکههای اجتماعی، سیستمهای مسیریابی و بهینهسازی توزیع منابع. با استفاده از الگوریتم فلوید، میتوان بهبود زمان سفر، مصرف سوخت، بهرهوری عمومی و بهینهسازی فرآیندها را در این حوزهها ایجاد کرد.
الگوریتم فلوید چیست؟
الگوریتم فلوید یک الگوریتم ریاضی است که برای یافتن کوتاهترین مسیرها بین همه جفت نقاط در یک گراف استفاده میشود. این الگوریتم بر اساس مفهوم برنامهریزی پویا عمل میکند و با بهروزرسانی ماتریس فاصله بین نقاط، کوتاهترین مسیرها را تعیین میکند.
الگوریتم فلوید چه کاربردهایی دارد؟
الگوریتم فلوید در بسیاری از حوزهها کاربرد دارد؛ به عنوان مثال، در شبکههای حمل و نقل برای برنامهریزی مسیرها، در شبکههای اجتماعی برای تحلیل شبکهها و رفتار افراد، در سیستمهای مسیریابی برای تعیین مسیرهای کوتاهتر، و در بهینهسازی شبکههای توزیع برق و غیره استفاده میشود.
الگوریتم فلوید چگونه کار میکند؟
الگوریتم فلوید با استفاده از یک ماتریس فاصله، ماتریس مسیر و بهروزرسانیهای متعدد، کوتاهترین مسیرها را محاسبه میکند. ابتدا ماتریس فاصله اولیه را تعیین کرده و سپس با تکرار بهروزرسانی ماتریسها، مسیرهای کوتاهتر را شناسایی میکند تا به ماتریس نهایی کوتاهترین مسیرها برسد.
پیچیدگی زمانی الگوریتم فلوید چگونه است؟
پیچیدگی زمانی الگوریتم فلوید برابر با $\mathrm{O}\left({\mathrm{n}}^{\mathrm{3}}\right)$ است، که $\mathrm{n}$ تعداد نقاط در گراف را نشان میدهد. به این معنی که زمان اجرای الگوریتم با افزایش تعداد نقاط افزایش مییابد.
آیا الگوریتم فلوید قابلیت کار با وزنهای منفی دارد؟
بله، الگوریتم فلوید میتواند با وزنهای منفی نیز کار کند. در واقع، این الگوریتم بهطور معمول برای گرافهایی که شامل وزنهای منفی هستند نیز استفاده میشود.