الگوریتم فلوید وارشال چیست، آموزش الگوریتم فلوید وارشال

الگوریتم فلوید-وارشال الگوریتمی برای یافتن کوتاه‌ترین مسیر بین تمام جفت رئوس در یک گرافگراف چیست، آموزش گراف از 0 تا 100 توسط دانشجو ارشد صنعتی شریفدر این مقاله تمامی مطالب مربوط به گراف از 0 تا 100 تدریس شده است. مواردی همچون : گراف چیست؟ انواع گراف، گراف همبند، مکمل گراف،‌ گراف کامل، گراف جهت دار، گراف بدون جهت،‌ گراف ساده و ... وزن‌دار است. این الگوریتمالگوریتم چیست به زبان ساده و با مثال های فراواندر این مقاله به زبان بسیار ساده و با مثال های متعدد توضیح داده شده که الگوریتم چیست و چه کاربردهایی دارد برای گراف‌های وزن دار جهت‌دار و بدون جهت کار می‌کند، اما برای گراف‌هایی با دور منفی (که مجموع یال‌های یک دور، منفی است) کار نمی‌کند. در این آموزش نحوه عملکرد الگوریتم فلوید-وارشال را خواهید آموخت؛ همچنین نمونه‌های پیاده‌سازی از الگوریتم فلوید-وارشال را در پایتونزبان برنامه نویسی پایتون چیست؟ – نحوه شروع و دلایل محبوبیتزبان برنامه نویسی پایتون (Python) چیست؟ این مقاله عالی به بررسی دلایل محبوبیت پایتون، موارد استفاده از پایتون و نحوه شروع به برنامه نویسی پایتون پرداخته، جاواجاوا چیست؟ تعریف، معنی و ویژگی های جاوا (java) از 0تا100جاوا یک زبان برنامه نویسی همه منظوره، مبتنی بر کلاس و شی گرا است که برای داشتن وابستگی های پیاده سازی کمتر طراحی شده است، زبان برنامه نویسی جاوا شبیه ++C است، Cزبان برنامه نویسی C – مزایا و کاربرد زبان C – فرق C و ++Cاین مقاله عالی ابتدا توضیح می‌دهد که زبان برنامه نویسی c چیست، سپس به بررسی مزایا و معایب زبان C ، کاربردهای زبان سی ، و تفاوت بین C و ++C می‌پردازد و سی پلاس پلاسبرنامه نویسی سی پلاس پلاس چیست؟ مزایای برنامه نویسی C++‎؟برنامه نویسی سی پلاس پلاس چیست و چه کاربردی دارد؟ این صفحه عالی به بررسی مزایای برنامه نویسی C++ پرداخته و نمونه هایی از کدهای زبان برنامه نویسی ++C را آورده خواهید دید.

نحوه کارکرد الگوریتم فلوید وارشال با مثال

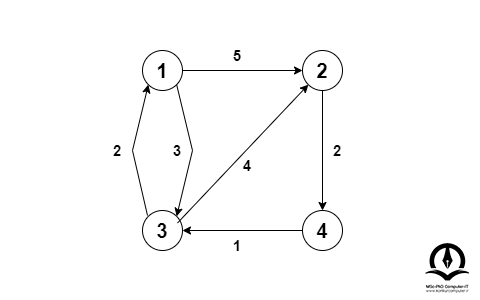
در ادامه الگوریتم فلوید وارشال را با ارائه یک مثال بررسی می‌کنیم. گراف زیر را در نظر بگیرید:

یک ماتریسماتریس در ساختمان داده⚡️معرفی انواع ماتریس (خلوت،قطری)این مقاله عالی گفته ماتریس چیست و به آموزش ماتریس پرداخته، همچنین انواع ماتریس از جمله ماتریس خلوت، ماترس قطری و ماتریس های بالا و پایین مثلثی را معرفی کرده ${\mathrm{A}}_0$ با بعد $\mathrm{n*n}$ ایجاد کنید که n تعداد رئوس گراف است. سطر و ستون به ترتیب به صورت i و j نمایش داده می‌شوند. i و j رئوس گراف هستند. هر خانه ${\mathrm{A}}_{\left[\mathrm{i}\right]\left[\mathrm{j}\right]}$ با فاصله رأس i تا رأس j پر شده است. اگر مسیری از رأس i ام به رأس j ام وجود نداشته باشد، مقادر اندیس بی‌نهایت باقی می‌ماند.

${\mathrm{A}}_0\mathrm{=}\left[\mathrm{0\ \ 3\ \ }\mathrm{\infty }\mathrm{\ \ 5\ \ 2\ \ 0\ \ }\mathrm{\infty }\mathrm{\ \ 4\ \ }\mathrm{\infty }\mathrm{\ \ 1\ \ 0\ \ }\mathrm{\infty }\mathrm{\ \ }\mathrm{\infty }\mathrm{\ \ }\mathrm{\infty }\mathrm{\ \ 2\ \ 0}\right]$

حال با استفاده از ماتریس ${\mathrm{A}}_0$ یک ماتریس ${\mathrm{A}}_1$ ایجاد کنید. عناصر ستون اول و سطر اول به همان صورت باقی می‌مانند. اندیس‌های باقی‌مانده به روش زیر پر می‌شوند.

فرض کنید k رأس میانی در کوتاه‌ترین مسیر از مبدأ تا مقصد باشد. در این مرحله k اولین راس است. ${\mathrm{A}}_{\left[\mathrm{i}\right]\left[\mathrm{j}\right]}$ با $\left({\mathrm{A}}_{\left[\mathrm{i}\right]\left[\mathrm{k}\right]}\mathrm{+}{\mathrm{A}}_{\left[\mathrm{k}\right]\left[\mathrm{j}\right]}\right)$ پر می‌شود اگر $\left({\mathrm{A}}_{\left[\mathrm{i}\right]\left[\mathrm{j}\right]}\mathrm{>}{\mathrm{A}}_{\left[\mathrm{i}\right]\left[\mathrm{k}\right]}\mathrm{+}{\mathrm{A}}_{\left[\mathrm{k}\right]\left[\mathrm{j}\right]}\right)$. یعنی اگر فاصله مستقیم از مبدأ تا مقصد بیشتر از مسیر عبور از رأس k باشد، آنگاه اندیس با مقدار ${\mathrm{A}}_{\left[\mathrm{i}\right]\left[\mathrm{k}\right]}\mathrm{+}{\mathrm{A}}_{\left[\mathrm{k}\right]\left[\mathrm{j}\right]}$ پر می‌شود. در این مرحله k رأس 1 است. فاصله رأس مبدأ تا رأس مقصد را از طریق راس k محاسبه می‌کنیم.

${\mathrm{A}}_{\mathrm{1}}\mathrm{=}\left[\mathrm{0\ \ 3\ \ }\mathrm{\infty }\mathrm{\ \ 5\ \ 2\ \ 0\ \ 9\ \ 4\ \ }\mathrm{\infty }\mathrm{\ \ 1\ \ 0\ \ 8\ \ }\mathrm{\infty }\mathrm{\ \ }\mathrm{\infty }\mathrm{\ \ 2\ \ 0}\right]\mathrm{\ \ \ \ \ \ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ \ \ \ \ \ }{\mathrm{A}}_{\mathrm{1}}\mathrm{=}\left[\mathrm{0\ \ 3\ \ }\mathrm{\infty }\mathrm{\ \ 5\ \ 2\ \ 0\ \ 0\ \ 0}\right]$

به عنوان مثال: برای ${\mathrm{A}}_{\mathrm{1}}\mathrm{=}\left[\mathrm{2,}\mathrm{\ }\mathrm{4}\right]$، فاصله مستقیم از رأس 2 تا 4 برابر 4 است و مجموع فاصله از رأس 2 تا 4 از طریق رأس (یعنی از رأس 2 به 1 و از رأس 1 تا 4) برابر است با 7. از آن‌جایی که $7>4$، ${\mathrm{A}}_{\mathrm{1}}\mathrm{=}\left[\mathrm{2,}\mathrm{\ }\mathrm{4}\right]$ با 4 پر می‌شود. به طور مشابه، ${\mathrm{A}}_2$ با استفاده از ${\mathrm{A}}_1$ ایجاد می‌شود. عناصر ستون دوم و سطر دوم به همان صورت باقی می‌مانند. در این مرحله k رأس دوم (یعنی رأس 2) است. مراحل باقی‌مانده مانند مرحله 2 است.

${\mathrm{A}}_{\mathrm{2}}\mathrm{=}\left[\mathrm{0\ \ 3\ \ 9\ \ 5\ \ 2\ \ 0\ \ 9\ \ 4\ \ 3\ \ 1\ \ 0\ \ 5\ \ }\mathrm{\infty }\mathrm{\ \ }\mathrm{\infty }\mathrm{\ \ 2\ \ 0}\right]\mathrm{\ \ \ \ \ \ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ \ \ \ \ \ }{\mathrm{A}}_{\mathrm{2}}\mathrm{=}\left[0\mathrm{\ \ 3\ \ 2\ \ 0\ \ 9\ \ 4\ \ 1\ \ 0\ \ }\mathrm{\infty }\mathrm{\ \ 0}\right]$

بطور مشابه ${\mathrm{A}}_3$ و ${\mathrm{A}}_4$ را هم می‌سازیم:

${\mathrm{A}}_{\mathrm{3}}\mathrm{=}\left[\mathrm{0\ \ 3\ \ 9\ \ 5\ \ 2\ \ 0\ \ 9\ \ 4\ \ 3\ \ 1\ \ 0\ \ 5\ \ 5\ \ 3\ \ 2\ \ 0}\right]\mathrm{\ \ \ \ \ \ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ \ \ \ \ \ }{\mathrm{A}}_{\mathrm{3}}\mathrm{=}\left[\mathrm{0\ \ }\mathrm{\infty }\mathrm{\ \ 0\ \ 9\ \ }\mathrm{\infty }\mathrm{\ \ 1\ \ 0\ \ 8\ \ 2\ \ 0}\right]$

${\mathrm{A}}_{\mathrm{4}}\mathrm{=}\left[\mathrm{0\ \ 3\ \ 7\ \ 5\ \ 2\ \ 0\ \ 6\ \ 4\ \ 3\ \ 1\ \ 0\ \ 5\ \ 5\ \ 3\ \ 2\ \ 0}\right]\mathrm{\ \ \ \ \ \ \ \ }\mathrm{\Rightarrow }\mathrm{\ \ \ \ \ \ \ \ }{\mathrm{A}}_{\mathrm{4}}\mathrm{=}\left[\mathrm{0\ \ 5\ \ 0\ \ 4\ \ 0\ \ 5\ \ 5\ \ 3\ \ 2\ \ 0}\right]$

${\mathrm{A}}_4$ کوتاه‌ترین مسیر را بین هر جفت رئوس نشان می‌دهد.

پیاده سازی الگوریتم فلوید وارشال

حال که با نحوه کارکرد الگوریتم فلوید-وارشال آشنا شدیم، ابتدا شبه کد آن و سپس پیاده‌سازی این الگوریتم با زبان های برنامه نویسیزبان های برنامه نویسی چیست؟این مقاله عالی توضیح داده که زبان های برنامه نویسی چیست؟ و انواع زبان های برنامه نویسی و بهترین زبان برنامه نویسی برای شروع و پردرآمدترین آنها را معرفی کرده مختلف را خواهیم دید.

Pseudo Code

n = no of vertices
A = matrix of dimension n*n
for k = 1 to n
  for i = 1 to n
    for j = 1 to n
      Ak[i, j] = min (Ak-1[i, j], Ak-1[i, k] + Ak-1[k, j])
return A

n = no of vertices
A = matrix of dimension n*n
for k = 1 to n
  for i = 1 to n
    for j = 1 to n
      Ak[i, j] = min (Ak-1[i, j], Ak-1[i, k] + Ak-1[k, j])
return A

کپی کردن کد

Python

# Floyd Warshall Algorithm in python


# The number of vertices
nV = 4

INF = 999


# Algorithm implementation
def floyd_warshall(G):
  distance = list(map(lambda i: list(map(lambda j: j, i)), G))

  # Adding vertices individually
  for k in range(nV):
    for i in range(nV):
      for j in range(nV):
        distance[i][j] = min(distance[i][j], distance[i][k] + distance[k][j])
  print_solution(distance)


# Printing the solution
def print_solution(distance):
  for i in range(nV):
    for j in range(nV):
	  if(distance[i][j] == INF):
        print("INF", end=" ")
      else:
        print(distance[i][j], end="  ")
      print(" ")


G = [[0, 3, INF, 5],
     [2, 0, INF, 4],
     [INF, 1, 0, INF],
     [INF, INF, 2, 0]]
floyd_warshall(G)

# Floyd Warshall Algorithm in python


# The number of vertices
nV = 4

INF = 999


# Algorithm implementation
def floyd_warshall(G):
  distance = list(map(lambda i: list(map(lambda j: j, i)), G))

  # Adding vertices individually
  for k in range(nV):
    for i in range(nV):
      for j in range(nV):
        distance[i][j] = min(distance[i][j], distance[i][k] + distance[k][j])
  print_solution(distance)


# Printing the solution
def print_solution(distance):
  for i in range(nV):
    for j in range(nV):
	  if(distance[i][j] == INF):
        print("INF", end=" ")
      else:
        print(distance[i][j], end="  ")
      print(" ")


G = [[0, 3, INF, 5],
     [2, 0, INF, 4],
     [INF, 1, 0, INF],
     [INF, INF, 2, 0]]
floyd_warshall(G)

کپی کردن کد

Java

// Floyd Warshall Algorithm in Java

class FloydWarshall {
  final static int INF = 9999, nV = 4;

  // Implementing floyd warshall algorithm
  void floydWarshall(int graph[][]) {
    int matrix[][] = new int[nV][nV];
    int I, j, k;

    for (I = 0; I < nV; i++)
      for (j = 0; j < nV; j++)
        matrix[i][j] = graph[i][j];

    // Adding vertices individually
    for (k = 0; k < nV; k++) {
      for (I = 0; I < nV; i++) {
        for (j = 0; j < nV; j++) {
          if (matrix[i][k] + matrix[k][j]  matrix[i][j])
            matrix[i][j] = matrix[i][k] + matrix[k][j];
        }
      }
    }
    printMatrix(matrix);
  }

  void printMatrix(int matrix[][]) {
    for (int I = 0; I < nV; ++i) {
      for (int j = 0; j < nV; ++j) {
        if (matrix[i][j] == INF)
          System.out.print(“INF “);
        else
          System.out.print(matrix[i][j] + “  “);
      }
      System.out.println();
    }
  }

  public static void main(String[] args) {
    int graph[][] = { { 0, 3, INF, 5 }, { 2, 0, INF, 4 }, { INF, 1, 0, INF }, { INF, INF, 2, 0 } };
    FloydWarshall a = new FloydWarshall();
    a.floydWarshall(graph);
  }
}

// Floyd Warshall Algorithm in Java

class FloydWarshall {
  final static int INF = 9999, nV = 4;

  // Implementing floyd warshall algorithm
  void floydWarshall(int graph[][]) {
    int matrix[][] = new int[nV][nV];
    int I, j, k;

    for (I = 0; I < nV; i++)
      for (j = 0; j < nV; j++)
        matrix[i][j] = graph[i][j];

    // Adding vertices individually
    for (k = 0; k < nV; k++) {
      for (I = 0; I < nV; i++) {
        for (j = 0; j < nV; j++) {
          if (matrix[i][k] + matrix[k][j]  matrix[i][j])
            matrix[i][j] = matrix[i][k] + matrix[k][j];
        }
      }
    }
    printMatrix(matrix);
  }

  void printMatrix(int matrix[][]) {
    for (int I = 0; I < nV; ++i) {
      for (int j = 0; j < nV; ++j) {
        if (matrix[i][j] == INF)
          System.out.print(“INF “);
        else
          System.out.print(matrix[i][j] + “  “);
      }
      System.out.println();
    }
  }

  public static void main(String[] args) {
    int graph[][] = { { 0, 3, INF, 5 }, { 2, 0, INF, 4 }, { INF, 1, 0, INF }, { INF, INF, 2, 0 } };
    FloydWarshall a = new FloydWarshall();
    a.floydWarshall(graph);
  }
}

کپی کردن کد

C

// Floyd-Warshall Algorithm in C

#include <stdio.h>

// defining the number of vertices
#define nV 4

#define INF 999

void printMatrix(int matrix[][nV]);

// Implementing floyd warshall algorithm
void floydWarshall(int graph[][nV]) {
  int matrix[nV][nV], i, j, k;

  for (i = 0; i < nV; i++)
    for (j = 0; j < nV; j++)
      matrix[i][j] = graph[i][j];

  // Adding vertices individually
  for (k = 0; k < nV; k++) {
    for (i = 0; i < nV; i++) {
      for (j = 0; j < nV; j++) {
        if (matrix[i][k] + matrix[k][j]  matrix[i][j])
          matrix[i][j] = matrix[i][k] + matrix[k][j];
      }
    }
  }
  printMatrix(matrix);
}

void printMatrix(int matrix[][nV]) {
  for (int i = 0; i < nV; i++) {
    for (int j = 0; j < nV; j++) {
      if (matrix[i][j] == INF)
        printf("%4s", "INF");
      else
        printf("%4d", matrix[i][j]);
    }
    printf("\n");
  }
}

int main() {
  int graph[nV][nV] = {{0, 3, INF, 5},
             {2, 0, INF, 4},
             {INF, 1, 0, INF},
             {INF, INF, 2, 0}};
  floydWarshall(graph);
}

// Floyd-Warshall Algorithm in C

#include <stdio.h>

// defining the number of vertices
#define nV 4

#define INF 999

void printMatrix(int matrix[][nV]);

// Implementing floyd warshall algorithm
void floydWarshall(int graph[][nV]) {
  int matrix[nV][nV], i, j, k;

  for (i = 0; i  nV; i++)
    for (j = 0; j  nV; j++)
      matrix[i][j] = graph[i][j];

  // Adding vertices individually
  for (k = 0; k  nV; k++) {
    for (i = 0; i  nV; i++) {
      for (j = 0; j  nV; j++) {
        if (matrix[i][k] + matrix[k][j]  matrix[i][j])
          matrix[i][j] = matrix[i][k] + matrix[k][j];
      }
    }
  }
  printMatrix(matrix);
}

void printMatrix(int matrix[][nV]) {
  for (int i = 0; i  nV; i++) {
    for (int j = 0; j  nV; j++) {
      if (matrix[i][j] == INF)
        printf("%4s", "INF");
      else
        printf("%4d", matrix[i][j]);
    }
    printf("\n");
  }
}

int main() {
  int graph[nV][nV] = {{0, 3, INF, 5},
             {2, 0, INF, 4},
             {INF, 1, 0, INF},
             {INF, INF, 2, 0}};
  floydWarshall(graph);
}

کپی کردن کد

C++

// Floyd-Warshall Algorithm in C++

#include <iostream>
using namespace std;

// defining the number of vertices
#define nV 4

#define INF 999

void printMatrix(int matrix[][nV]);

// Implementing floyd warshall algorithm
void floydWarshall(int graph[][nV]) {
  int matrix[nV][nV], i, j, k;

  for (i = 0; i < nV; i++)
    for (j = 0; j < nV; j++)
      matrix[i][j] = graph[i][j];

  // Adding vertices individually
  for (k = 0; k < nV; k++) {
    for (i = 0; i < nV; i++) {
      for (j = 0; j < nV; j++) {
        if (matrix[i][k] + matrix[k][j]  matrix[i][j])
          matrix[i][j] = matrix[i][k] + matrix[k][j];
      }
    }
  }
  printMatrix(matrix);
}

void printMatrix(int matrix[][nV]) {
  for (int i = 0; i < nV; i++) {
    for (int j = 0; j < nV; j++) {
      if (matrix[i][j] == INF)
        printf("%4s", "INF");
      else
        printf("%4d", matrix[i][j]);
    }
    printf("\n");
  }
}

int main() {
  int graph[nV][nV] = {{0, 3, INF, 5},
             {2, 0, INF, 4},
             {INF, 1, 0, INF},
             {INF, INF, 2, 0}};
  floydWarshall(graph);
}

// Floyd-Warshall Algorithm in C++

#include <iostream>
using namespace std;

// defining the number of vertices
#define nV 4

#define INF 999

void printMatrix(int matrix[][nV]);

// Implementing floyd warshall algorithm
void floydWarshall(int graph[][nV]) {
  int matrix[nV][nV], i, j, k;

  for (i = 0; i < nV; i++)
    for (j = 0; j < nV; j++)
      matrix[i][j] = graph[i][j];

  // Adding vertices individually
  for (k = 0; k < nV; k++) {
    for (i = 0; i < nV; i++) {
      for (j = 0; j < nV; j++) {
        if (matrix[i][k] + matrix[k][j]  matrix[i][j])
          matrix[i][j] = matrix[i][k] + matrix[k][j];
      }
    }
  }
  printMatrix(matrix);
}

void printMatrix(int matrix[][nV]) {
  for (int i = 0; i < nV; i++) {
    for (int j = 0; j < nV; j++) {
      if (matrix[i][j] == INF)
        printf("%4s", "INF");
      else
        printf("%4d", matrix[i][j]);
    }
    printf("\n");
  }
}

int main() {
  int graph[nV][nV] = {{0, 3, INF, 5},
             {2, 0, INF, 4},
             {INF, 1, 0, INF},
             {INF, INF, 2, 0}};
  floydWarshall(graph);
}

کپی کردن کد

پیچیدگی زمانی و فضایی الگوریتم فلوید وارشال

در این الگوریتم سه حلقه وجود دارد. هر حلقهحلقه در برنامه نویسی چیست؟ حلقه یا لوپ (Loop) چیست؟این مقاله عالی به زبان ساده و با استفاده از فیلم توضیح داده که حلقه در برنامه نویسی چیست، همچنین در خصوص حلقه یا لوپ (Loop) بی نهایت صحبت کرده است پیچیدگی‌های ثابتی دارد بنابراین، پیچیدگی زمانیپیچیدگی زمانی الگوریتم چیست؟ معرفی نماد های مجانبیاین صفحه عالی به معرفی پیچیدگی زمانی الگوریتم پرداخته، همچنین انواع نماد های مجانبی و پیچیدگی زمانی های برخی از الگوریتم های مرتب سازی و جستجو را توضیح داده  الگوریتم فلوید-وارشال $\mathrm{O}\left({\mathrm{n}}^{\mathrm{3}}\right)$ است. پیچیدگی فضایی الگوریتم فلوید-وارشال $\mathrm{O}\left({\mathrm{n}}^{\mathrm{2}}\right)$ است.

مقایسه الگوریتم فلوید وارشال و الگوریتم بلمن فورد

الگوریتم بلمن-فورد یک الگوریتم برای پیدا کردن کوتاه‌ترین مسیر از یک مبدأ است که با ریلکس کردن مکرر یال‌ها در گراف کار می‌کند، تا زمانی که کوتاه‌ترین مسیر برای همه رئوس پیدا شود. این الگوریتم به ویژه برای گراف‌هایی با یال‌های با وزن منفی کاربردی است، زیرا می تواند دورهای منفی را تشخیص دهد. در حالی که الگوریتم فلوید-وارشال یک الگوریتم برای یافتن کوتاه‌ترین مسیر از چند مبدأ است که با محاسبه کوتاه‌ترین مسیر بین تمام جفت‌های رئوس در گراف با استفاده از برنامه نویسی پویابرنامه نویسی پویا چیست، برنامه نویسی پویا در طراحی الگوریتماین صفحه عالی به معرفی برنامه نویسی پویا یا Dynamic programming پرداخته و کاربردها و مثال هایی از برنامه نویسی پویا در طراحی الگوریتم آورده است  کار می‌کند.

کاربردهای الگوریتم فلوید وارشال

الگوریتم فلوید-وارشال کاربردهای زیادی دارد که از بین آن‌ها می‌توان به موارد زیر اشاره کرد:

• یافتن کوتاه‌ترین مسیر یک گراف جهت دار
• یافتن بسته بودن نسبت به تعدی گراف‌های جهت دار
• پیدا کردن وارون ماتریس‌ها
• آزمایش دوبخشی بودن یک گراف بدون جهت

جمع‌بندی

الگوریتم فلوید-وارشال، الگوریتمی برای مسائل کوتاه‌ترین مسیر بین تمام جفت‌های رئوس در یک گراف است. این الگوریتم از رویکرد برنامه نویسی پویا برای یافتن کوتاه‌ترین مسیر پیروی می‌کند. در این مقاله به بررسی این الگوریتم پرداختیم و مثالی برای درک بهتر این الگوریتم ارائه کردیم؛ همچنین به بررسی پیچیدگی مرتبه زمانی و فضایی این الگوریتم پرداختیم و این الگوریتم را با استفاده از زبان‌های برنامه‌نویسی مختلف پیاده‌سازی کردیم.

مطالب مرتبط

همه مقالات

ساختمان داده چیست؟ آموزش ساختمان داده به زبان ساده

نصب آناکوندا روی ویندوز ⚡️ دانلود و نحوه نصب آناکوندا

انواع مختلف CSS ⚡️ تعاریف، مزایا و معایب آن ها

زبان CSS چیست و چه کاربردی دارد؟⚡️سی اس اس چیست