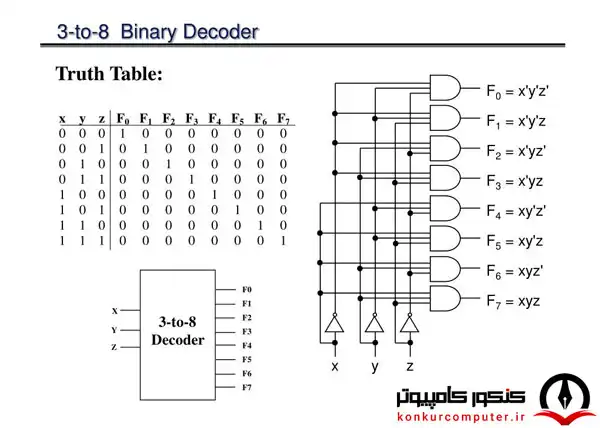
در مدار منطقی مدارات به دو دسته مدارات ترکیبی و مدارات ترتیبی تقسیم می‌شوند، مدارات ترکیبی زیادی در مدار منطقی نظیر مالتی پلکسر، مقایسه کننده، انکدر، دیکدر، دی مالتی پلکسر، جمع کننده و ... وجود دارد، ما در این صفحه قصد داریم به بررسی دیکودر (Decoder) بعنوان یکی از مدارات ترکیبی بپردازیم، برای بررسی سایر مدارات ترکیبی و ترتیبی به صفحه مدار منطقیآموزش مدار منطقی به زبان ساده - بررسی مدار منطقی و انواع آن
امروزه درک صحیحی از مدارهای منطقی برای هر مهندس برق و کامپیوتر ضروری است. این مدارها عنصر اصلی کامپیوترها و بسیاری از وسایل الکترونیکی اطراف ما هستند، در این صفحه به بررسی و آموزش مدار منطقی پرداخته شده است مراجعه کنید. همچنین می‌دانیم که افرادی که برای طراحی و معماری کامپیوتر داشتن دانش مدار منطقی واجب است، شما عزیزان برای مطالعه بیشتر در مورد معماری کامپیوتر آموزش جامع معماری کامپیوتر
در مهندسی کامپیوتر، معماری کامپیوتر مجموعه‌ای از قوانین و روش‌هایی است که به چگونگی طراحی، کارکرد، سازماندهی و پیاده سازی (ساخت) سیستم‌های کامپیوتری می‌پردازد، در این صفحه به بررسی و آموزش کامل معماری کامپیوتر پرداخته شده است نیز می‌توانید به صفحه مذکور مراجعه کنید.
در مدار منطقی دیکدر مداری است با n ورودی و \(2^n\) خروجی که بسته به ترکیب سیگنال ورودی آن، در یک لحظه با فرض فعال بودن پایه enable دیکدر، تنها یکی از پایه‌های خروجی فعال خواهد بود. خروجی دیکدر مینترم‌های n متغیر ورودی آن است. دیکودرها دارای انواع 2 به 4، 3 به 8، 4 به 16 و ... هستند. مدار دیکودر می‌تواند شامل یک سیگنال فعال ساز (En) باشد. اگر سیگنال فعال‌ساز غیر فعال باشد، مدار دیکدر غیرفعال خواهد شد و عمل نخواهد کرد.
فیلم معرفی کامل دیکودر
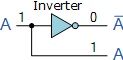
یک دیکدر 1 به 2 را می‌توان با استفاده از یک گیت NOT مطابق شکل زیر طراحی کرد.
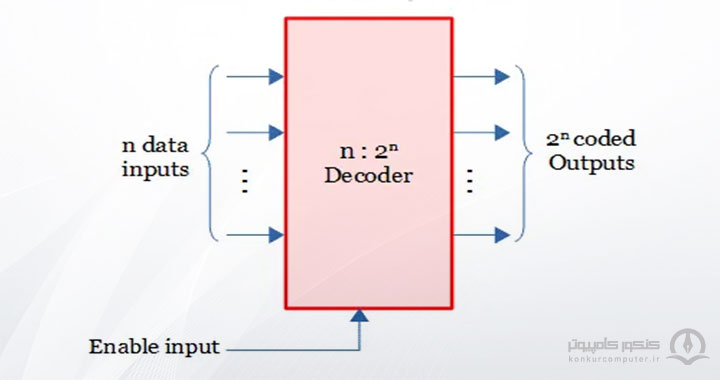
ساختار کلی یک دیکدر در شکل زیر آورده شده است.
یکی از انواع مختلف دیکدرها، دیکدر BCD به دهدهی است که دارای 10 بیت خروجی است. ورودی آن اعداد دهدهی کد شده به باینری در رنج 0 تا 9 است، که هر کدام از این ورودی‌ها یکی از 10 پایه ورودی منحصر به فرد خروجی را فعال می‌سازد. اگر ورودی غیر از آنچه گفته شد به دیکدر داده شود هیچ کدام از خروجی‌ها فعال نخواهند شد.
دیکدر باینری 2 به 4
یک دیکدر 2 به 4 همانطور که از نام آن پیداست دارای 2 پایه ورودی و 4 پایه خروجی است. البته دیکودر می‌تواند یک پایه ورودی دیگر نیز به نام Enable داشته باشد که در ادامه آن را توضیح خواهیم داد. بلوک دیگرام یک دیکدر 2 به 4 و طراحی مدار آن در شکل‌های زیر آورده شده است.
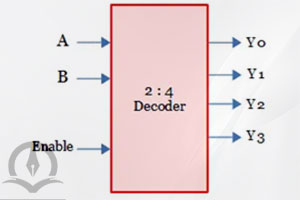
با توجه به اینکه به ورودی‌های A و B چه مقداری بدهیم، فقط یکی از پایه‌های خروجی در هر لحظه فعال و سایر پایه‌ها غیر فعال خواهند بود.
اگر خروجی‌های دیکودر Active High باشد منظور از فعال 1 و اگر Active Low باشند منظور از فعال 0 است. توجه کنید که در یک قطعه هر یک از پایه‌های ورودی و پایه‌های خروجی می‌توانند Active high یا Active Low باشند.
در زیر می‌خواهیم حالتی را بررسی کنیم که هم پایه‌های وروردی یعنی A و B و پایه Enable(EN) و هم پایه‌های خروجی Active High هستند.
دو پایه A و B، دو ورودی گفته شده دیکدر هستند و $y_{\ 0}$ تا $y_{\ 4}$ پایه‌های خروجی این دیکدر هستند که مینترم‌های دو ورودی داده شده را تولید می‌کنند. اگر پایه Enable(EN) مقدار 1 داشته باشد دیکدر فعال است و خروجی دیکدر موارد مورد انتظار ما خواهد بود ولی اگر پایه Enable(EN) مقدار 0 را داشته باشد، تمامی خروجی‌ها غیر فعال و مقدار 0 خواهند داشت.
در جمله بالا گفته شد که خروجی های این دیکودر مینترم‌ها را تولید می‌کنند، توجه کنید که اگر پایه‌های خروجی دیکودر Active High باشند، خروجی‌های دیکودر مینترم‌ها را تولید می‌کند ولی اگر پایه‌های خروجی دیکودر Active Low باشند، خروجی‌های دیکودر ماکسترم‌ها را تولید می‌کنند.
از آنجایی که دیکدر ما با 1 بودن پایه Enable(EN) فعال بوده و یکی از خروجی‌های آن مقدار 1 و سایر خروجی‌ها مقدار 0 داشته و با 0 بودن پایه Enable(EN) غیر فعال و همگی خروجی‌ها مقدار 0 را خواهند داشت.
جدول درستی این دیکدر 2 به 4 برای درک بهتر در شکل زیر آورده شده است.
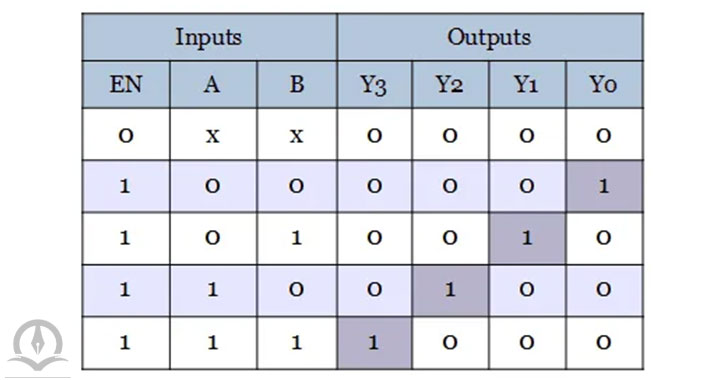
با توجه به جدول درستی بالا می‌توان تابع هر کدام از پایه‌های خروجی را به صورت زیر به دست آورد، که همانطور که مشخص است، هر یک از پایه‌های خروجی یکی از مینترم‌ها را تولید می‌کند.
\[Y_0=E\bar{A}\bar{B}\]
\[Y_1=E\bar{A}B\]
\[Y_2=EA\bar{B}\]
\[Y_3=EAB\]
مدار داخلی یک دیکودر 2 به 4 به شکل زیر است، همانطور که در شکل مدار دیکدر 2 به 4 مشخص است، هرکدام از گیت‌های AND یکی از مینترم‌ها را تولید می‌کند:
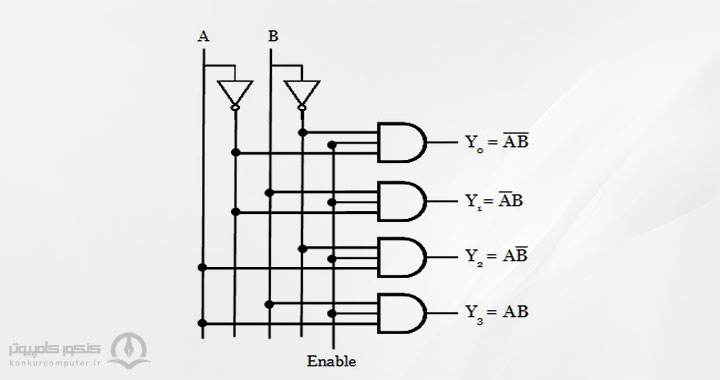
علاوه بر طراحی منطقی ذکر شده می‌توان یک دیکدر 2 به 4 را با استفاده از گیت NAND نیز مطابق شکل زیر ساخت.
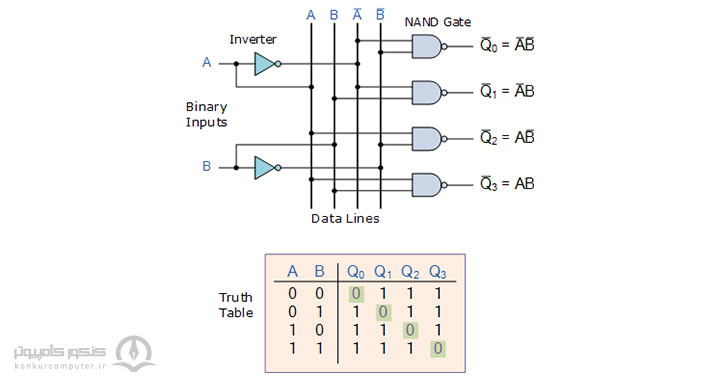
این دیکدر Active Low است به بیان دیگر یعنی تنها یک پایه‌ی خروجی LOW یا 0 بوده و سایر پایه‌ها HIGH یا 1 هستند.
به روش مشابه می‌توان دیکدرهای 3 به 8 و 4 به 16 را نیز طراحی کرد، در زیر به بررسی این موضوع می‌پردازیم.
بررسی دیکدر 3 به 8
یک دیکدر 3 به 8 همانطور که از نام آن پیداست دارای 2 پایه ورودی و 4 پایه خروجی است. جدول درستی این دیکدر 3 به 8 برای درک بهتر در زیر آورده شده است.
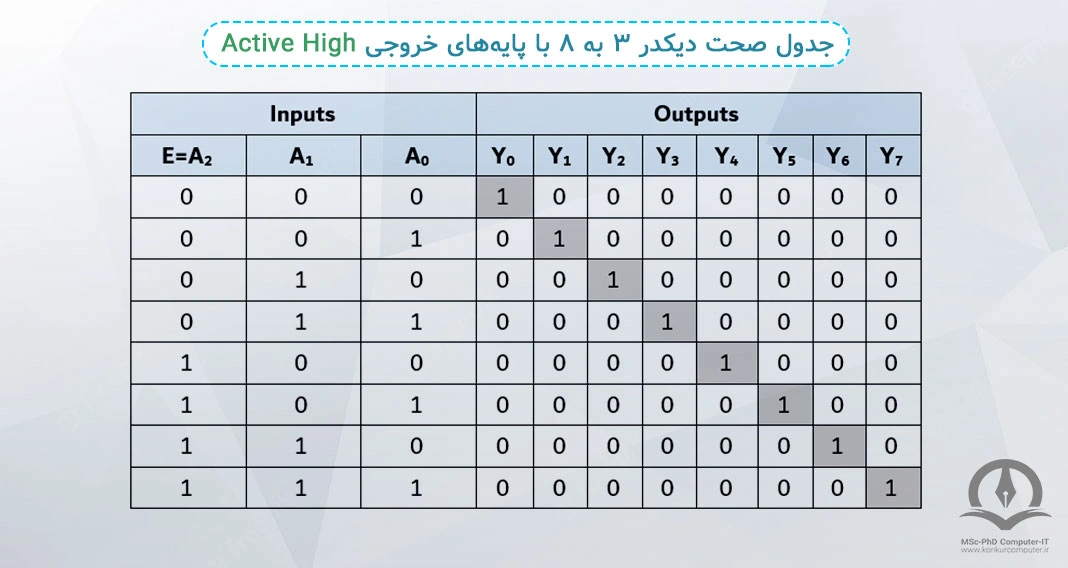
مدار داخلی یک دیکودر 3 به 8 به شکل زیر است، همانطور که در شکل مدار دیکدر 3 به 8 مشخص است، هرکدام از گیت‌های AND یکی از مینترم‌ها را تولید می‌کند:
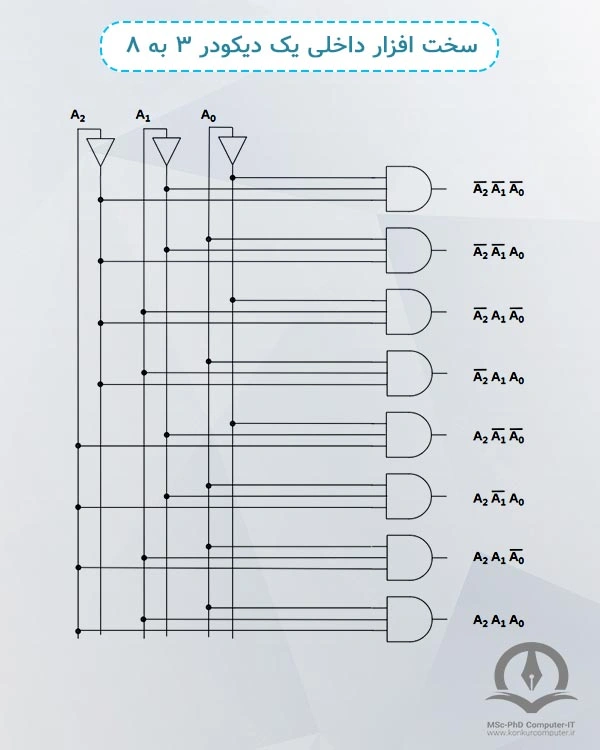
شکلی دیگر از بلکوک دیاگرام، جدول درستی و مدار داخلی دیکودر 3 به 8
طراحی دیکدر 3 به 8 با دیکدر 2 به 4
در این قسمت می‌خواهیم با استفاده از دو دیکدر 2 به 4 یک دیکدر 3 به 8 بسازیم. همان طور که می‌دانید یک دیکدر، n ورودی و 2n خروجی دارد و با توجه به اینکه خروجی دیکدر Active High است یا Active Low، در خروجی دیکدر، مینترم ها یا ماکسترم ها را تولید می‌شوند.
در شکل زیر ما دو دیکدر داریم که ورودی هر دوی آنها دو متغیر A0 و A1 می باشد و ارزش پایه A1 بیشتر از A0 است:
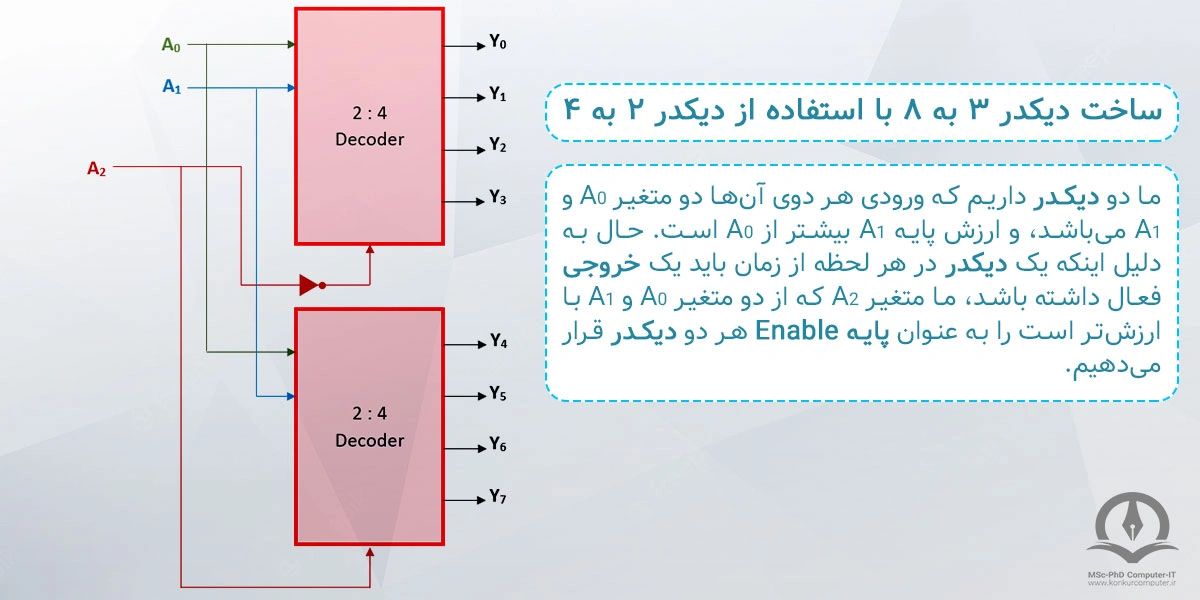
توجه کنید که یک دیکدر در هر لحظه از زمان باید یک خروجی فعال داشته باشد، از آن جایی که ما دو دیکودر داریم و هر یک از این دیکودرها یک خروجی فعال دارند بنابراین در هر لحظه شاهد دو خروجی فعال خواهیم بود، به منظور رفع این مشکل و رعایت این اصل که دیکودر کلی ما فقط باید یک پایه فعال داشته باشد، باید از پایه Enable استفاده کنیم که این کار موجب آن می‌شود که در صورت صفر و یا یک بودن این پایه (در اینجا پایه A2) مدار به کار عادی خودش ادامه دهد. (اینکه پایه Enable با با یک فعال است یا صفر، به Active High و Active Low بود آن پایه بستگی دارد).
به همین منظور ما متغیر A2 که از دو متغیر A0 و A1 با ارزش‌تر است را به عنوان پایه Enable هر دو قرار می‌دهیم، به گونه‌ای که در هر لحظه از زمان فقط یکی از دیکدر ها به کار عادی خودش ادامه دهد.
طراحی دیکدر 5 به 32 با دیکدر 3 به 8
ما برای طراحی دیکودر 5 به 32 به یک دیکدر 2 به 4 و چهار دیکودر 3 به 8 نیاز داریم (متغیر A4 به عنوان MSB و متغیر A0 نیز LSB است):
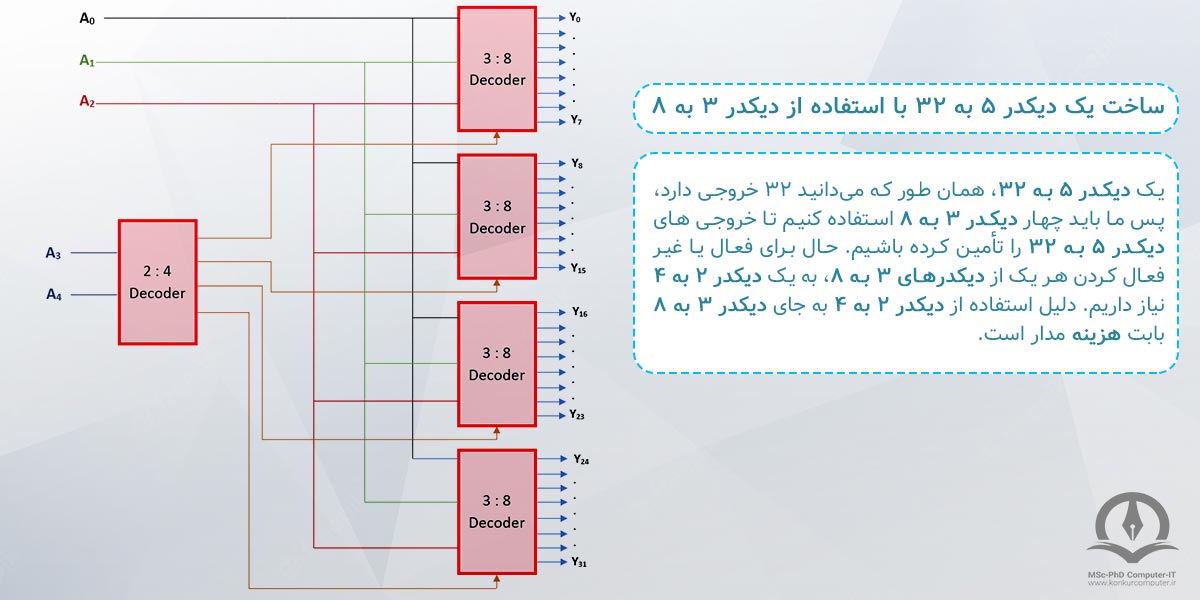
خروجی دیکدر 2 به 4 به پایه های Enable دیکدر های 3 به 8 متصل شده است، که این امر طبق موارد گفته شده در طراحی دیکودر 3 به 8 با دیکدر 2 به 4، باعث می‌شود که در هر لحظه از زمان فقط یکی از خروجی‌ها فعال باشد یا به عبارت دیگر در هر لحظه فقط یک دیکودر به کار عادی خودش ادامه دهد، اگر این کار را انجام نمی‌دادیم باعث می‌شد که هر یک از دیکدر ها یک خروجی فعال داشته باشند.
شاید برایتان سوال باشد که چرا ما A4 و A3 را به عنوان ورودی های دیکودر 2 به 4 و متغیر های A2، A1 و A0 را به عنوان ورودی دیکدر های 3 به 8 قرار دادیم، برای درک بهتر این موضوع، مثالی کوچکی را بررسی می‌کنیم. برای مثال فرض کنید می‌خواهیم یک دیکدر 3 به 8 بسازیم، ورودی هایی که خواهیم داشت به شکل زیر است:
| A0 | A1 | A2 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
اگر به مقادیر A0 نگاه کنید صفر و یک به صورت Periodic تکرار شده است:
| A0 |
|---|
| 0 |
| 1 |
| 0 |
| 1 |
| 0 |
| 1 |
| 0 |
| 1 |
چیزی که باعث تفاوت در این تکرار بیت ها می‌شود به زبان دیگر باعث تشخیص این تکرار می‌شود بیت سمت چپ آن یعنی A1 است:
| A0 | A1 |
|---|---|
| 0 | 0 |
| 1 | 0 |
| 0 | 1 |
| 1 | 1 |
| 0 | 0 |
| 1 | 0 |
| 0 | 1 |
| 1 | 1 |
و موردی که باعث تفاوت تکرار Periodic صفر و یک های A1 می‌شود A2 است:
| A1 | A2 |
|---|---|
| 0 | 0 |
| 0 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
به همین علت است که متغیرهای با ارزش را به عنوان ورودی‌های دیکدری که به عنوان فعال یا غیر فعال کننده دیگر دیکدرها است قرار می‌دهیم.
ساخت دیکدر 4 به 16 با دیکدر 2 به 4
پنج دیکدر 2 به 4 برای ساخت دیکودر 4 به 16 استفاده می‌شود، که به یکی از آنها برای اینکه توسط پایه های خروجی آن، پایه ی Enable چهار دیکدر دیگر را فعال یا غیر فعال کنیم، نیاز داریم:
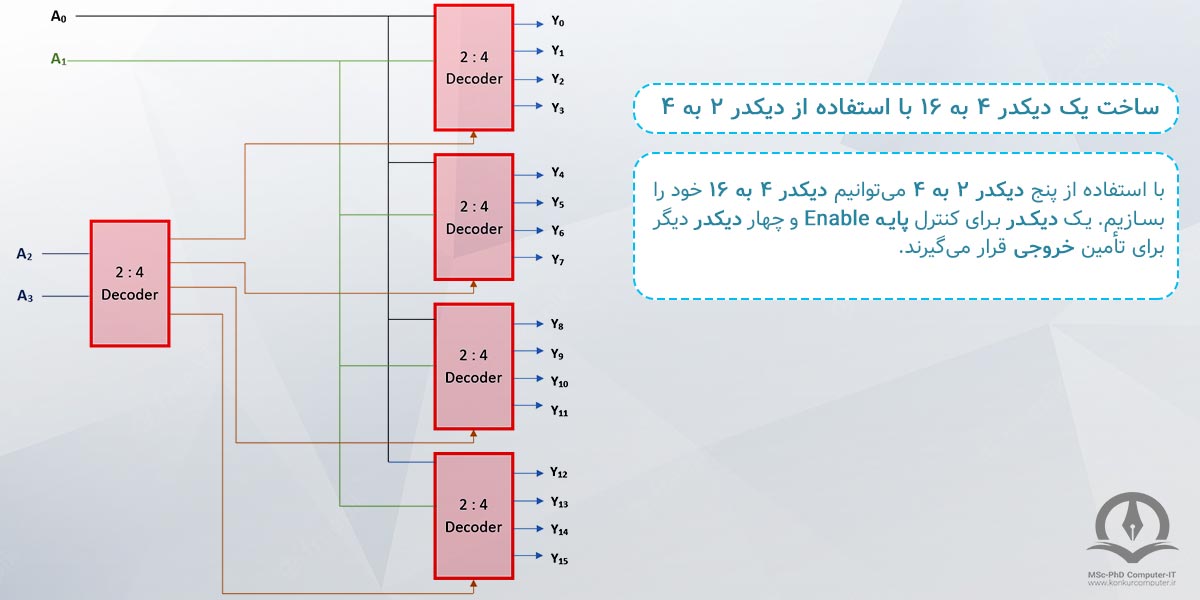
متغیرهای با ارزش ما (A3 و A2) به عنوان ورودی‌های دیکدر اول قرار گرفته است و دو متغیر (A1 و A0)نیز به عنوان ورودی‌های ۴ دیکودر دیگر در نظر گرفته شده است.
دیکدرهای آبشاری
می‌توان با اتصال دیکدرهای باینری کوچک، دیکدرهای باینری بزرگ‌تری را ساخت. برای مثال با استفاده از 2 دیکدر با 2 ورودی می‌توان یک دیکدر 4 ورودی طراحی کرد. و یا با اتصال 2 دیکدر 3 به 8 یک دیکدر 4 به 16 را طراحی کرد. به مثال زیر توجه کنید.
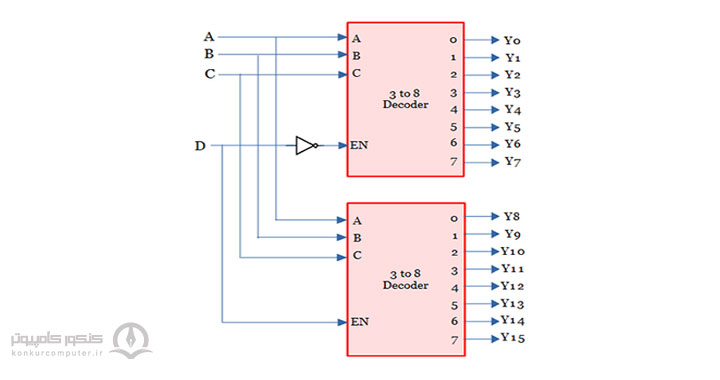
همانطور که در شکل بالا قابل مشاهده است در این مثال با ترکیب 2 دیکدر 3 به 8 یک دیکدر 4 به 16 ساخته شده است. برای به دست آوردن تعداد دیکدرهای مشابه کوچک‌تر برای طراحی یک دیکدر بزرگ می‌توان از فرمول زیر استفاده کرد:
\[\text{تعداد}\mathrm{\ }\text{دیکدرهای}\mathrm{\ }\text{مشابه}\mathrm{\ }\text{کوچک‌تر}\mathrm{\ =}\frac{\text{تعداد}\mathrm{\ }\text{خروجی‌های}\mathrm{\ }\text{دیکدر}\mathrm{\ }\text{بزرگ‌تر}}{\text{تعداد}\mathrm{\ }\text{خروجی‌های}\mathrm{\ }\text{دیکدر}\mathrm{\ }\text{کوچک‌تر}}\]
که در مثال ما برای طراحی یک دیکدر 4 به 16 با استفاده از دیکدرهای 3 به 8، به \(\frac{16}{8}=2 \) دیکدر 3 به 8 نیاز است. در بلوک دیاگرام آورده شده ورودی‌های A,B,C به طور مستقیم به هر دو دیکدر داده می‌شوند. ورودی D که دارای بالاترین مرتبه است. یکبار به صورت NOT به پایه EN یکی از دیکدرها متصل شده است. بنابراین این دیکدر 8 مینترم کم ارزش \((Y_7\ \text{تا} Y0)\) را تولید می‌کند. بار دیگر ورودی D به طور مستقیم به پایه EN دیکدر دیگر متصل می‌شود، و 8 مینترم پر ارزش \(Y_{15}\ \text{تا} Y8\) را تولید می‌کند.
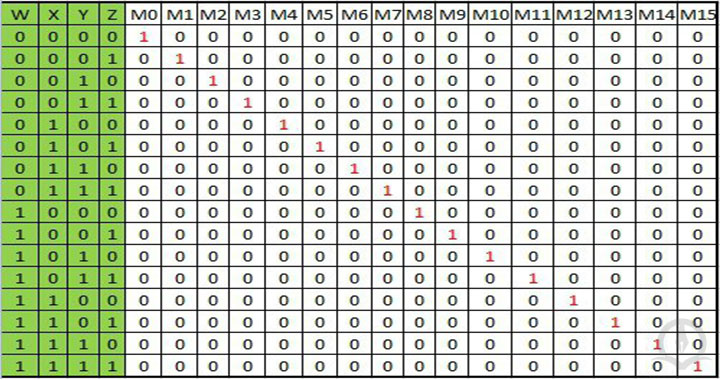
برای درک بهتر این موضوع به جدول درستی دیکدر 4 به 16 که در شکل زیر آورده شده است دقت کنید.
ICهای معروف با عملکرد دیکدر
IC 74138: عملکرد دیکدر 3 به 8 را ایفا می‌کند.
IC 74139: یک دیکدر دوگانه 2 به 4 است.
کاربردهای دیکودر
کاربردهای دیکدر به شرح زیر هستند :
- مبدل کد
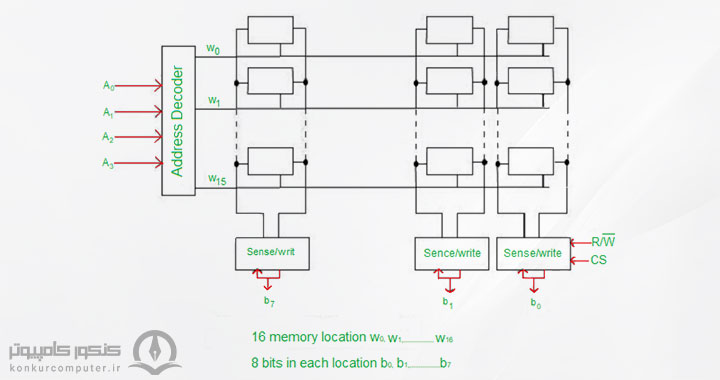
- در ساختار سیستم حافظه کامپیوتر جهت دسترسی به آدرس یک خانه مشخص از حافظه بر اساس آدرسی مشخص و معین استفاده می‌شود.
- برای انجام عملیات‌ها در واحد منطق پردازنده، از دیکدر برای رمزگشایی دستورالعمل‌های یک برنامه و فعال کردن خطوط کنترل مربوط به آن دستورالعمل استفاده می‌شود.
جمع بندی
مدارهای منطقی به‌دلیل سادگی در طراحی، بسیار پرکاربرد در سیستم‌های کامپیوتری هستند و می‌توان دلیل وجود کامپیوترها را ظهور دنیای منطقی و دیجیتال دانست. در این مقاله یکی از آی‌سی‌هایی که توسط این مدارهای منطقی ساخته شده‌اند را بررسی کردیم و متوجه سادگی و کاربردی بودن دیکدرها شدیم، بطور کلی می‌توان گفت کاربرد اصلی دیکدرها در فعالسازی خطوط خاص و معین است که در مدارهای زیادی مورد استفاده قرار می‌گیرد.
دیکودر چیست؟
برای مشاهده فیلم آموزش رایگان دیکودر به این صفحه مراجعه کنید. دیکودر یک قطعه ترکیبی است که آن را با علامت اختصاری DEC مشخص می‌کنند. یک DEC n/2n یک مدار ترکیبی بدون حافظه است که دارای n ورودی و 2n خروجی است، خروجی ها که تعداد آنها 2n تا است را از شماره 0 تا 2n-1 شماره گذاری می‌کنند. ورودی که تعداد آنها n تا است یک عدد باینری را مشخص می‌کند که چون این عدد n بیتی است مقدار آن از 0 تا 2n-1 است، که این عدد مشخص کننده شماره خروجی است که باید فعال شود.
کاربرد دیکدر چیست؟
دیکدر کاربردهای زیادی در جهان پیرامون ما دارد که از جمله آنها می‌توان به استفاده از آنها در خطوط شبکهِ شبکه های کامپیوتری، مبدل کدها، در شبکه تلفن، در ساختار سیستم حافظه های کامپیوتر، در واحد محاسبه و منطق درون پردازنده و در بسیاری از جاهای دیگه کاربرد دارد.
