برای شروع حرفهای کنکور ارشد کامپیوتر،آیتی و علوم کامپیوتر حتما روی عکس زیر کلیک کنید تا در کانال کنکور کامپیوتر عضو شوید، در این کانال به معرفی بهترین منابع کنکور ارشد،برنامه ریزی و مشاوره، معرفی گرایشها و هر آنچه برای موفقیت در کنکور ارشد نیاز دارید پرداخته شده است

ریاضیات (عمومی (1و2)، آمار و احتمال مهندسی، ریاضیات گسسته):
پاسخ تشریحی ریاضی 1و2 کنکور ارشد کامپیوتر 1401
طبق رابطه دوران در اعداد مختلط داریم:
$cos(n\alpha)+i\;sin(n\alpha)=(cos(a)+i\;sin(\alpha))^n$
با قرار دادن $\alpha=\frac{ \pi}{2}-\theta$ خواهیم داشت:
$cos(\frac{n \pi}{2}-n\theta)+i\;sin(\frac{n \pi}{2}-n\theta)=[cos(\frac{\pi}{2}-\theta)+i\;sin(\frac{\pi}{\theta})]^n =(sin\theta+i\;cos\theta)^n$
سمت راست عبارت صورت سوال همان سمت راست این عبارت است، برای اینکه سمت چپ ها هم مساوی باشد باید داشته باشیم:
\[\left\{ \begin{matrix} \cos\left( \frac{\text{nπ}}{2} - n\theta \right) = \sin\left( \text{nθ} \right) = \cos{\left( \frac{\pi}{2} - n\theta \right)(*)}\;\;\;\;\; \\ \sin\left( \frac{\text{nπ}}{2} - n\theta \right) = cos\left( \text{nθ} \right) = s\mathbb{i}n\left( \frac{\pi}{2} - n\theta \right)(*)(*) \\ \end{matrix} \right.\ \]
| \[\frac{\text{nπ}}{2} - n\theta = 2k\pi + \frac{\pi}{2} - n\theta\] | \[\mathrm{\nearrow }\] | \[(*) \Rightarrow \frac{\text{nπ}}{2} - n\theta = 2k\pi \pm \left( \frac{\pi}{2} - n\theta \right)\] |
| \[\frac{\text{nπ}}{2} - n\theta = 2k\pi - \frac{\pi}{2} + n\theta\] | \[\mathrm{\searrow }\] |
\[\Rightarrow \left\{ \begin{matrix} \frac{\text{nπ}}{2} = \left( 2k + \frac{1}{2} \right)\pi \Rightarrow n = 4k + 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ n\left( \frac{\pi}{2} - 2\theta \right) = \left( 2k - \frac{1}{2} \right)\pi \rightarrow \ \text{می شود و قابل قبول نیست} \; \theta\; \text{وابسته به} \;n \end{matrix} \right.\ \]
\[(**) \Rightarrow \left\{ \begin{matrix} \frac{\text{nπ}}{2} - n\theta = 2k\pi + \frac{\pi}{2} - n\theta \rightarrow n = 4k + 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{\text{nπ}}{2} - n\theta = (2k + 1)\pi - \frac{\pi}{2} + n\theta \rightarrow \text{می شود و قابل قبول نیست} \; \theta\; \text{وابسته به} \;n \\ \end{matrix} \right.\ \]
پس $n$ باید برابر $4k+1$ باشداما طبق صورت سوال داریم:
$1\le n\le1001\Rightarrow 1\le 4k+1\le1001\Rightarrow 0\le4k\le1000\Rightarrow0\le\ k\le250\Rightarrow \ k $تعداد$ =250-0+1=251$
با قاعده تبدیل تفاضل به حاصلضرب داریم:
$sinA-sinB=2cos\frac{A+B}{2}sin\frac{A-B}{2}$
با درنظر گرفتن $A=\sqrt{x+1}$ و $B=\sqrt{x}$ داریم:
$\lim_{x\to\infty}2cos\frac{(\sqrt{x+1}+\sqrt{x}}{2})sin\frac{(\sqrt{x+1}-\sqrt{x}}{2})$
اما برای عبارت داخل sin داریم:
$\lim_{x\to\infty }\frac{(\sqrt{x+1}+\sqrt{x}}{2})\lim_{x\to\infty }\frac{(x+1)-x}{2(\sqrt{n+1}+\sqrt{x})}\lim_{x\to\infty }\frac{1}{2(\sqrt{x+1}+\sqrt{x})}=0$
بنابراین حد حاصل برابر است با حاصلضرب یک مقدار کراندار در صفر که میشود صفر
با توجه به اینکه $0\le sin^2t\le1$ است داریم:
\[0 \leq \int_{0}^{x}{\frac{\sin^{2}t}{1 + t^{2}}\mathbb{d}t} \leq \int_{0}^{x}{\frac{1}{1 + t^{2}}\mathbb{d}t} = \left\lbrack \tan^{- 1}(t) \right\rbrack_{0}^{x} = \tan^{- 1}x \leq \frac{\pi}{2}\]
و چون تابع $\tan^{- 1}x$ کراندار است، تابع$F(x)$ هم کراندار میشود و داريم:
\[0 \leq F(x) \leq \frac{\pi}{2}\]
(رد گزينههاي 1 و 4)
بررسي اكسترمم:
\[F(x) = \int_{0}^{x}{\frac{\sin^{2}t}{1 + t^{2}}\mathbb{d}t} = \left\lbrack G(t) \right\rbrack_{0}^{x} = G(x) - G(0) \Rightarrow F^{'}(x) = G^{'}(x) = \left. \ \frac{\sin^{2}t}{1 + t^{2}} \right|_{x} = \frac{\sin^{2}x}{1 + x^{2}}\]
\[F^{'}(x) = 0 \Rightarrow \sin x = 0 \Rightarrow x = k\pi\]
نقاط $k\pi$ نقاط بحرانی است ولی اکسترمم نیست زیرا در این نقاط مشتق دوم هم صفر میشود زیرا:
\[F^{''}(x) = \frac{2\sin x\cos x\left( 1 + x^{2} \right) - 2x\sin^{2}x}{\left( 1 + x^{2} \right)^{2}} = \frac{2\sin x}{\left( 1 + x^{2} \right)^{2}}\left( \left( 1 + x^{2}\right)\cos x - x\sin x \right)\]
پس طبق آزمون مشتق دوم نقاط $x=k\pi$ نقاط عطف میشود و نه اکسترمم.
با توجه به بسط مک لورن $sinx$ داریم:
\[f(x) = \sum_{n = 0}^{\infty}{\frac{f^{(n)}(\theta)}{n!}x^{n}} \Rightarrow \sin x = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!}+ \ldots\]
مشاهده میشود که تمام جملات عبارت سوال در $x^2$ ضرب شده است پس داریم:
\[f(x) = x^{2}\sin x \Rightarrow f^{'}(x) = 2x\sin x + x^{2}cosx \Rightarrow f^{'}\left( \frac{\pi}{2} \right) = 2\left( \frac{\pi}{2} \right)\sin\frac{\pi}{2} + \left( \frac{\pi}{2} \right)^{2}\cos\frac{\pi}{2}\]
\[=2(\frac{\pi}{2})(1)+(\frac{\pi}{2})^2(0)=\pi\]
رابطه طول قوس منحنی $y=f(x)$ در بازه $[a,b]$ بصورت زیر است:
$L=\int_{a}^{b}\sqrt{1+[f^\prime(x)]^2}dx$
ابتدا مشتق تابع $f(x)$ را حساب میکنیم:
\[f(x) = ln\left( \frac{\mathbb{e}^{x} + 1}{\mathbb{e}^{x} - 1} \right) = \ln\left( \mathbb{e}^{x} + 1 \right) - \ln\left( \mathbb{e}^{x}- 1 \right)\]
\[\Rightarrow f^{'}(x) = \frac{\mathbb {e}^{x}}{\mathbb{e}^{x} + 1} - \frac{\mathbb{e}^{x}}{\mathbb{e}^{x} - 1} = \frac{- 2\mathbb{e}^{x}}{_{\mathbb{e}}^{2}x - 1} \Rightarrow \left\lbrack f^{'}(x) \right\rbrack^{2} = \frac{4\mathbb{e}^{2x}}{\left( \mathbb{e}^{2x} - 1 \right)^{2}} \]
\[\Rightarrow 1 + \left\lbrack f^{'}(x) \right\rbrack^ {2} = 1 + \frac{4\mathbb{e}^{2x}}{\left( \mathbb{e}^{2x} - 1 \right)^{2}} = \frac{\left( \mathbb{e}^{2x} - 1 \right)^{2} + 4\mathbb{e}^{2x}}{\left( e^{2x} - 1 \right)^{2}} = \frac{\left( \mathbb{e}^{2x} + 1 \right)^{2}}{\left( e^{2x} - 1 \right)^{2}} \]
\[\Rightarrow \sqrt {1 + \left\lbrack f^{'}(x) \right\rbrack^{2}} = \left| \frac{\mathbb{e}^{2x} + 1}{\mathbb{e}^{2x} - 1} \right| = \frac{\mathbb{e}^{2x} + 1}{\mathbb{e}^{2x} - 1}\ \text{( در بازه} \lbrack 1,2\rbrack \text{عبارت مثبت است )} \]
\[\Rightarrow L = \int_ {1}^{2}{\frac{\mathbb{e}^{2x} + 1}{\mathbb{e}^{2x} - 1}\mathbb{d}x} = \int_{1}^{2}{\left( \frac{2\mathbb{e}^{2x}}{e^{2x} - 1} - \frac{\mathbb{e}^{2x} - 1}{\mathbb{e}^{2x} - 1} \right)\mathbb{d}x} = \int_{1}^{2}{\frac{2\mathbb{e}^{2x}}{\mathbb{e}^{2x} - 1}\mathbb{d}x} - \int_{1}^{2}{\mathbb{d}x} \]
\[= \left\lbrack \ln\left( \mathbb {e}^{2x} - 1 \right) \right\rbrack_{1}^{2} - 1 = \ln\left( \mathbb{e}^{4} - 1 \right) - \ln\left( \mathbb{e}^{2} - 1 \right) - 1 = \ln\left( \frac{\mathbb{e}^{4} - 1}{\mathbb{e} - 1} \right) - 1\]
\[= \ln\left( \frac{\left( \mathbb {e}^{2} + 1 \right)\left( \mathbb{e}^{2} - 1 \right)}{\left( \mathbb{e}^{2} - 1 \right)} \right) - 1 = \ln\left( \mathbb{e}^{2} + 1 \right) - \ln\mathbb{e} = \ln\left( \frac{\mathbb{e}^{2} + 1}{\mathbb{e}} \right) = \ln\left( \mathbb{e} + \frac{1}{\mathbb{e}}\right)\]
$f(x,y)=\begin{cases} \frac{x}{x-y} & x \not= 0 \\ 0 & x = y \end{cases}$
طبق تعریف مشتق سویی، مشتق جهت دار در نقطه $(x_0,y_0)$و در جهت $\vec{u}(a,b)$ برابر است با:
\[\lim_ {t \rightarrow 0}\frac{f\left( x_{0} + ta,y_{0} + tb \right) - f\left( x_{0},y_{0} \right)}{t} \]
با توجه به اینکه $f(0,0) = 0$ مشتق جهتدار در این نقطه و در جهت $\vec{u}(a,b)$ را بررسی میکنیم:
\[\lim_ {t \rightarrow 0}\frac{f(ta,tb) - 0}{t} = \left\{ \begin{matrix} \ \ \ \ \ \ \ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a = b \\ \frac{a}{t(a - b)}\ \ \ \ \ \ \ \ a \neq b \\ \end{matrix} \right.\ \]
پس برای اینکه مشتق موجود باشد یا باید $a=b$ باشد و یا $a=0$ باشد در غیر اینصورت مشتق موجود نیست.
$a=b\Rightarrow \vec{\ u}=a\vec{\ i}+b\vec{\ j}=a(\vec{\ i}+\vec{\ j})||\vec{\ i}+\vec{\ j}$
$a=0\Rightarrow \vec{\ u}=b\vec{\ j}||\vec{\ j}$
پاسخ تشریحی آمار و احتمال کنکور ارشد کامپیوتر 1401
2, 8, 3, 7, 0, 6, 1, 3, 4, 2, 1, 3, 0, 1, 5, 2, 3, 1, 0, 4
ابتدا دادهها را به صورت صعودی مرتب میکنیم:
0,0,0,1,1,1,1,2,2,2,3,3,3,3,4,4,5,6,7,8
برای محاسبه صدک $P$اُم از روابط زیر استفاده میکنیم که در آن $n$ تعداد دادههاست:
$r=[(n+1)p]=[21\times0.85]=[17.85]=17$
$w=(n+1)p-r=17.85-17=0.85$
$Q_p=(1-w)x_r+wx_{r+1}$
که در آن $x_r$ و $x_{r+1}$ بهترتیب $r$ اُمین و $(r+1)$ اُمین عنصر پس از مرتب سازی است که در اینجا داریم:
$Q_p=(1-0.85)x_{17}+(0.85)x_{18}=(0.15)5+(0.85)6=5.85$
با استفاده از قاعده احتمال شرطی داریم:
$P(E|F)=\frac{P(E\cap F)}{P(F)}\Rightarrow 0.8=\frac{P(E\cap F)}{0.6}\Rightarrow P(E\cap F)=0.48$
با رسم نمودار ون داریم:
| \[P(E - F) = P(E) - P(E \cap F) = 0.6 - 0.48 = 0.12\] \[P(F - E) = P(F) - P(E \cap F) = 0.6 - 0.48 = 0.12\] \[P(E \cup F) = 0.6 + 0.6 - 0.48 = 0.72\] \[P(E \cup F)^{'} = P\left( E^{'} \cap F^{'} \right) = 1 - 0.72 = 0.28 \] | 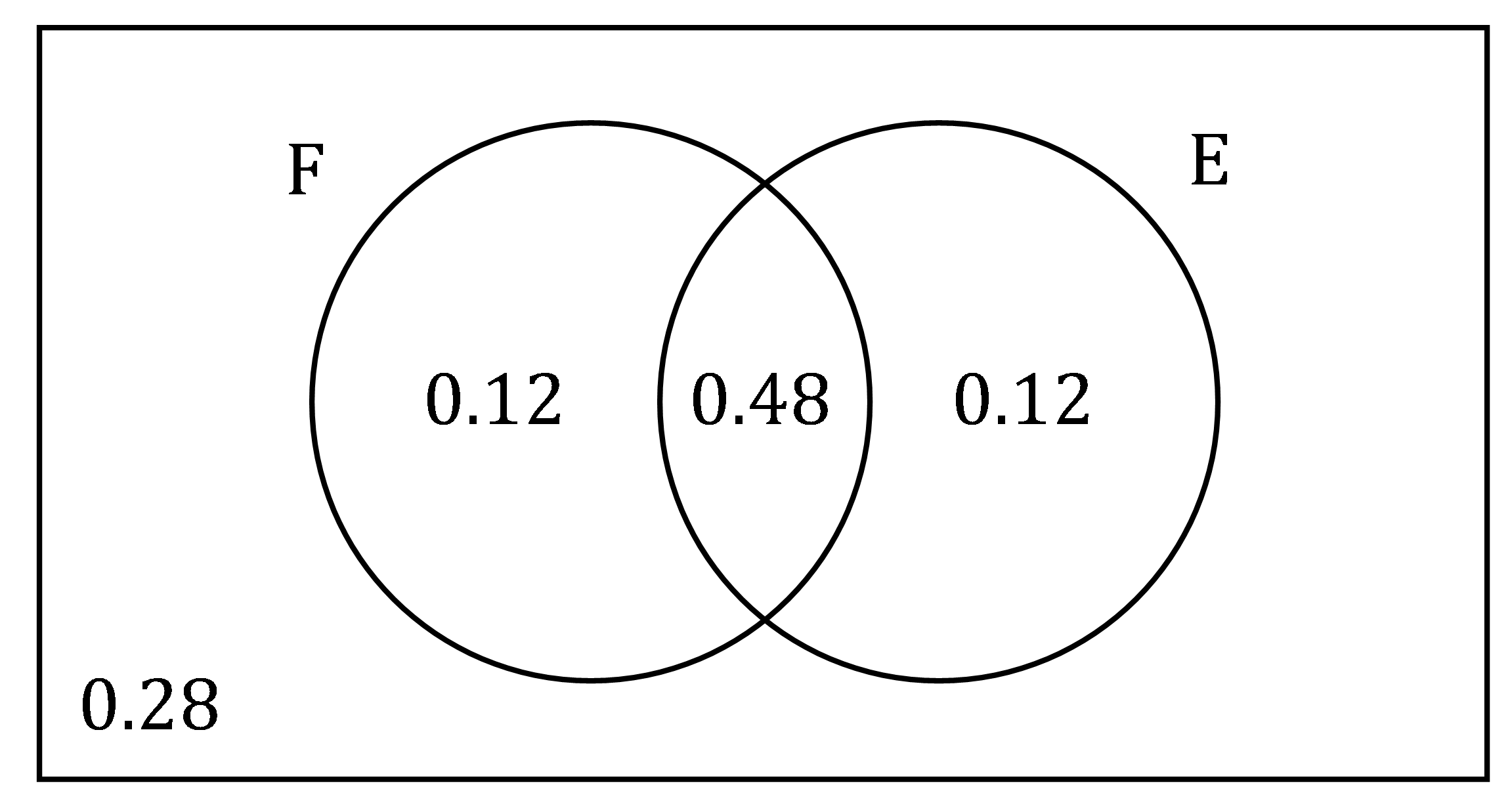 |
حال با این اطلاعات گزینه ها را بررسی میکنیم
\[P\left( \left. \ E \right|F^ {c} \right) = \frac{P\left( E \cap F^{'} \right)}{P\left( F^{'} \right)} = \frac{P(E - F)}{1 - P(F)} = \frac{0.12}{1 - 0.6} = \frac{0.12}{0.4} = 0.3\]
(رد گزینههای 1 و 2)
\[P\left( \left. \ E^ {c} \right|F^{c} \right) = \frac{P\left( E^{'} \cap F^{'} \right)}{P\left( F^{'} \right)} = \frac{0.28}{0.4} = 0.7\]
(رد گزینه 3 و پذیرش گزینه 4)
طبق صورت سوال، هرخال حداقل یک بار مشاهده میشود، چون تعداد پرتابها هفت تا است فقط در صورتی امکان پذیر است که یک خال دو بار مشاهده شده باشد و بقیه خالها فقط یک بار. تعداد حالتها برابر میشود با انتخاب ${7 \choose 6}$ و سپس جایگشت $6!$ و آزاد گذاشتن تاس باقیمانده و چون یک خال تکراری است تقسیم بر $2!$ یعنی:
تعداد کل حالات $= \frac {{ 7\choose 6}6!\times6}{2!}= \frac {7\times6!\times6}{2}$
کل حالات نیز برابر است با $6^7$ پس احتمال برابر است با:
$\frac{7\times6!\times6}{2\times6^7}=\frac {7\times6!}{2\times6^6}$
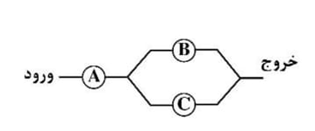
سیستم وقتی کار میکند که A حتما کار کند و B یا C حداقل یکی کار کند یعنی:
$P[(A\cap[B\cup C])]$
چون A از$B\cup C$ مستقل است داریم:
$=P(A).P(B\cup C)=p(A).[P(B)+P(C)-P(B\cap C)]$
و چون C و B مستقل هستند:
$=P(A).[P(B)+P(C)-P(B).P(C)]=0.9(1.8-0.81)=0.891$
ابتدا امید (میانگین) هر متغیر را محاسبه میکنیم
$E(x)=\int_{-\infty}^{+\infty} xf(x)=\int_0^1 2x^2\,dx = \frac{2x^3}{3}\Bigg|_0^1=\frac{2}{3} $
چون تعداد متغیرها زیاد است (بزرگتر از 30) توزیع حاصل تقریبا نرمال میشود و میانگین آن برابر است با مجموع میانگین توزیعها یعنی
$60\times \frac{2}{3}=40$
پس داریم:
$P(X>40)=P(Z> \frac {40-40}{\sigma})=P(Z>0)=0.5$
با توجه به صورت سوال $0 \ < t < \infty$ است، با مشتق گرفتن از تابع توزیع، تابع چگالی احتمال را بهدست میآوریم و از روی تابع چگالی احتمال، میانگین را محاسبه میکنیم
\[F_ {T}(t) = 1 - a\mathbb{e}^{- \lambda t} - (1 - a)e^{- \mu t} \]
\[f_ {t}(t) = \frac{\mathbb{d}F_{T}(t)}{\mathbb{d}t} = a\lambda e^{- \lambda t} + (1 - a)\mu e^{- \mu t} \]
\[\Rightarrow E(t) = \int_ {0}^{\infty}{\text{tf}(t)\mathbb{d}t} = a\lambda\int_{0}^{\infty}{t\mathbb{e}^{- \lambda t}\mathbb{d}t} + (1 - a)\mu\int_{0}^{\infty}{t\mathbb{e}^{- \mu t}\mathbb{d}t} \]
\[= a\lambda\left\lbrack \left( - \frac {t}{\lambda} - \frac{1}{\lambda^{2}} \right)\mathbb{e}^{- \lambda t} \right\rbrack_{0}^{\infty} + (1 - a)\mu\left\lbrack \left( - \frac{t}{\mu} - \frac{4}{\mu^{2}} \right)\mathbb{e}^{- \mu t} \right\rbrack_{0}^{\infty} \]
\[= a\lambda\left( \frac{1}{\lambda^{2}} \right) + (1 - a)\mu\left( \frac{1}{\mu^{2}} \right) = \frac{a}{\lambda} + \frac{1 - a}{\mu}\]
| x | ||||
| 3 | 2 | 1 | y | |
| 0.1 | 0.15 | 0.25 | 1 | |
| 0.1 | 0.35 | 0.05 | 2 | |
با جمع سطرها و ستونها جدول را کامل میکنیم
| x | |||||
| $\sum$ | 3 | 2 | 1 | ||
| 0.5 | 0.1 | 0.15 | 0.25 | 1 | y |
| 0.5 | 0.1 | 0.35 | 0.05 | 2 | |
| 1 | 0.2 | 0.5 | 0.3 | $\sum$ | |
طبق جدول احتمال شرطی داریم:
$P(X=1|Y=2)=\frac {P(X=1\cap Y=2)}{P(Y=2)}=\frac {0.05}{0.5}=0.1$
پاسخ تشریحی ریاضیات گسسته کنکور ارشد کامپیوتر 1401
راه حل عددگذاری: به ازای دوتاس $(n=2)$ تعداد حالتهای مختلف برابر است با تعداد اعضای قطر اصلی + نیمه بالایی (یا پایینی) ماتریس $6*6$ که برابر است با:
$6+\frac {36-6}{2}=6+15=21$
تنها گزینهای که جواب صحیح را بهازای $n=2$ میدهد گزینه 4 است
\[\begin{pmatrix} 2 + 5 \\ 2 \\ \end{pmatrix} = \begin{pmatrix} 7 \\ 2 \\ \end{pmatrix} = \frac{7 \times 6}{2} = 21\]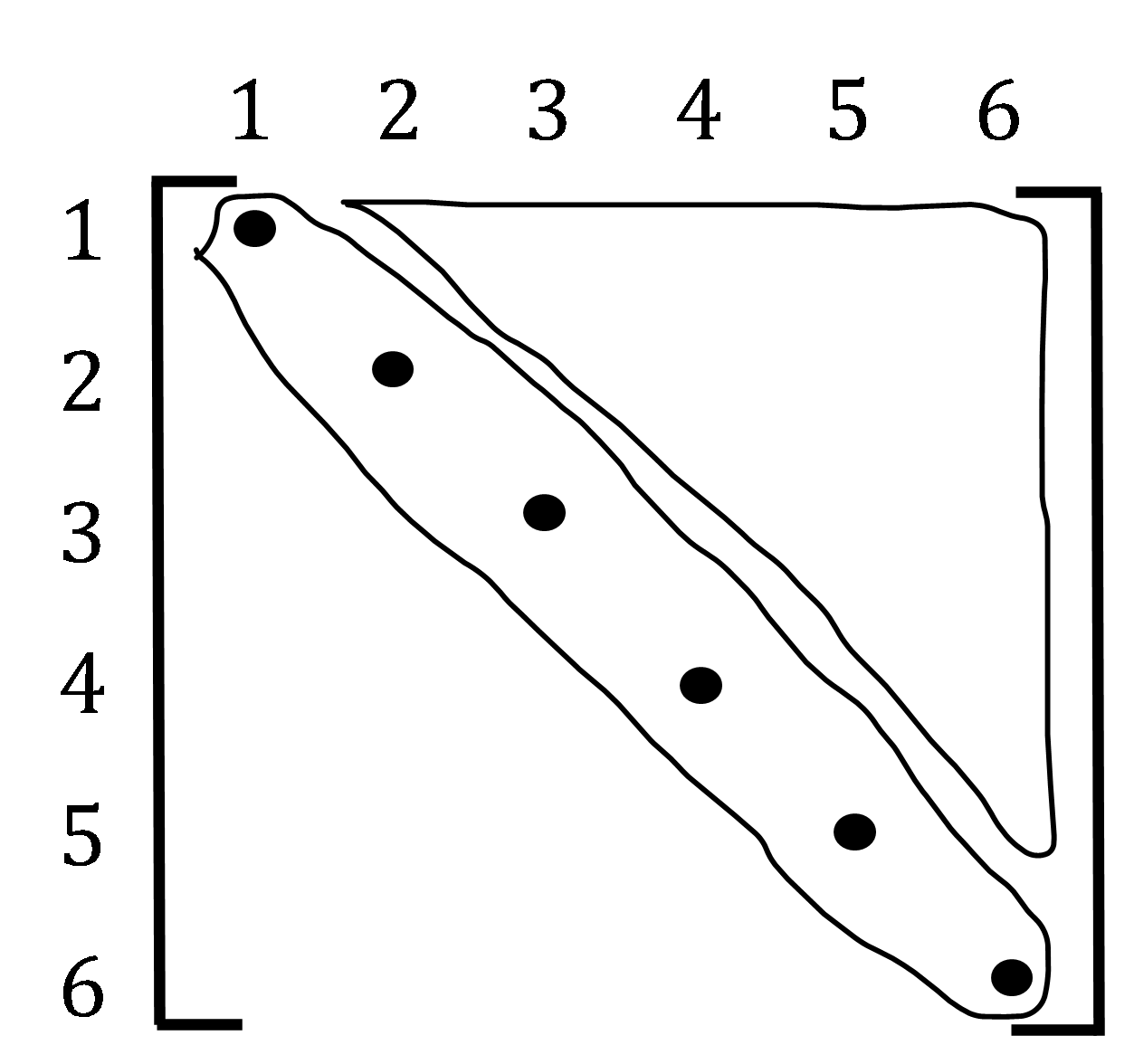
راه حل کلی: اگر $(1\le i\le 6)x_i$تعداد تاسهایی باشد که عدد $i$ رو شده باشد داریم:
$x_1+x_2+x_3+x_4+x_5+x_6=n \;\;\; x_i\ge 0$
تعداد جوابهای صحیح و نامنفی این معادله برابر است با:
${n+6-1\choose 5}={n+5\choose 5}={n+5\choose (n+5)-5}={n+5\choose n}$
الف) $\neg (\exists x[P(x)\wedge Q(x)])\equiv \forall x[P(x)\rightarrow \neg Q(x)]$
ب) $((P\rightarrow q)\wedge ((q\wedge r)\rightarrow s)\wedge r \rightarrow (P\rightarrow s)\equiv true$
بررسی گزاره الف: برای نقیض کردن سور وجودی، سور به عمومی تغییر میکند و گزاره جلوی آن نقیض میشود:
$\sim (\ni x,A(x))\equiv \forall x,\sim A(x)$
در نتیجه:
$\sim (\ni x,[P(x)\wedge Q(x)])\equiv \forall x,\sim P(x)\vee \sim Q(x) $
$\equiv \forall x, P(x)\rightarrow \sim Q(x) $
پس گزاره الف درست است
بررسی گزاره ب: باید ببینیم آیا استدلال مقابل معتبر است یا خیر:
$P\rightarrow q$
$(q\wedge r)\rightarrow s$
$r$
![]() $P\rightarrow s$
$P\rightarrow s$
گزاره میانی هم ارز با $\sim (q\wedge r)\vee s\equiv \sim q\; \vee \sim r\vee s$است.
و چون $\sim r$ نادرست است پس $\sim q\vee s$ درست است که این هم همارز با $q\rightarrow s$ است. از درستی$\begin{cases} P\rightarrow q & \\ \\ q\rightarrow s & \end{cases} $درستی$P\rightarrow s$ نتیجه میشود، پس گزاره ب هم درست است.
الف) مجموعه تمام دنبالههای اکیدأ صعودی از اعداد طبیعی شمارا است.
ب) مجموعه تمام دنبالههای اکیدا نزولی از اعداد طبیعی شمارا است.
مجموعه دنبالههای اکیدا نزولی از اعداد طبیعی شمار است زیرا با انتخاب اولین عدد دنباله، بقیه اعداد محدود میشوند، روش شمارش بصورت زیر است:
$\{1\},\{2\},\{2,1\},\{3\},\{3,2\},\{3,2,1\}\{3,1\},\{4\},\{4,3\},...$
اما مجموعه دنبالههای اکیدا صعودی نظم مشخصی ندارد و با انتخاب اولین عدد دنباله، هر عدد بزرگتر از آن عدد میتواند عدد بعدی باشد پس ناشماراست.
فرض کنیم که عدد 1 در جایگاه شماره $i$ باشد، دراینصورت برای جایگاه عدد $i$ دو حالت داریم:
1) عدد $i$ در جایگاه 1 باشد، دراینصورت بقیه اعداد به $D_{n-2}$ حالت میتوانند جایگشت بگیرند.
2) عدد $i$ در جایگاه 1 نباشد، دراینصورت $n-1$ عدد داریم که $i$ نباید در مکان 1 باشد و هر عدد دیگری نباید در مکان خودش باشد پس تعداد روشهای قرار گرفتن این $n-1$ عدد برابر تعداد پریشهای $n-1$عنصر یا همان $D_{n-1}$ است پس:
$D_n=(n-1)(D_{n-2}+D_{n-1})$
الف) به ازای هر عدد طبیعی دلخواه مانندk، اعداد $2k+1$ و $9k+4$ نسبت به هم اول هستند.
ب) معادله $(n-1)!+1=n^2$ در مجموعه اعداد طبیعی تنها یک جواب دارد.
بررسی گزاره الف: فرض میکنیم بمم دو عدد$2k+1$ و $9k+4$ برابر d باشد:
$d=(2k+1,9k+4)\Rightarrow \begin{cases} d|2k+1\Rightarrow |d|9(2k+1)\Rightarrow d|18k+9 \\ d|9k+4\Rightarrow d|2(9k+4)\Rightarrow d|18k+8 \end{cases}$
d باید تفاضل این دو مقدار را نیز عاد کند:
$d|\Rightarrow d=1$
پس این دو عدد نسبت به هم اولند و گزاره الف صحیح است.
بررسی گزاره ب: رشد دنباله $(n-1)!+1$سریعتر از $n^2$ است، به ازای $n=5$ این معادله صادق است زیرا $4!+1=5^2$ و به ازای $n>5$ آنقدر رشد دنباله سمت چپ زیاد میشود که هرگز دو عبارت مساوی نمیشوند پس تنها جواب طبیعی این معادله $n=5$ است و این گزاره هم صحیح است.
$xSy\leftrightarrow xRy\vee yRx$
کدام مورد در خصوص گزارههای زیر به ترتیب، درست است؟
الف) اگر R ترایایی باشد، آنگاه S نیز لزوما ترایایی است.
ب) اگر R همارزی باشد، آنگاه S نیز لزوما همارزی است.
بررسی گزاره الف: نادرستی گزاره را با یک مثال نقض نشان میدهیم. در این شکل R ترایایی است اما S ترایایی نیست. زیرا:
| \[aRb \rightarrow aSb\] \[\require{enclose} \Rightarrow a \enclose{horizontalstrike}{S}c \] \[cRb \rightarrow bSc\] | 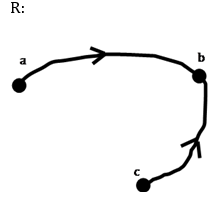 |
ولی a با c در رابطه S نیست.
بررسی گزاره ب: اگر R همارزی باشد بازتابی است، تقارنی است و ترایایی است
بازتابی است R : $\forall x \in A,xRx \rightarrow xSx \rightarrow \text{بازتابی است} \;S$
\[:\forall x,y \in A,xSy\ \Rightarrow \left\{ \begin{matrix} xRy \rightarrow yRx \rightarrow ySx \\ yRx \rightarrow ySx\ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix}\left. \ \begin{matrix} \ \\ \ \\ \end{matrix} \right\} \Rightarrow \text{تقارنی است}\text{ S} \right.\ \]
رابطه S بنا به تعریف خود همواره تقارنی است.
اما اگر R هم زمان هم ترایایی و هم تقارنی باشد، S نیز ترایایی میشود و نقص گزاره الف را برطرف میکند. پس S هرسه شرط را دارد و همارزی است.
روش دیگر بیان همارزی S:
R همارزی است پس مجموعه A را افراز میکند، با توجه به تعریف S، رابطه S هم مجموعه A را به همان زیرمجموعه هایی که R افراز کرد، افراز خواهد کرد پس S همارزی است.
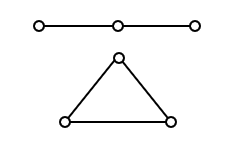
با یک مثال نقض 2 گزینه را رد میکنیم، گراف پنج ضلعی منتظم شرایط مسأله را ارضا میکند ![]() درجه تمام رأسها برابر 2 است $(k=2)$
درجه تمام رأسها برابر 2 است $(k=2)$
گزینههای 3 و 4 رد میشوند (این گراف حداقل 8 یال ندارد و دوبخشی هم نیست)
به راحتی دیده میشود که با تشکیل شبکهای از پنج ضلعی ها میتوان یالها و راسها را افزایش داد درنتیجه گزینه 1 هم رد ميشود.
دروس تخصصی 1 (نظریه زبانها و ماشینها، سیگنالها و سیستمها):
پاسخ تشریحی نظریه زبان ها و ماشین ها کنکور ارشد کامپیوتر 1401
- هر زبان تشخیصناپذیر تورینگ، تصمیمناپذیر است.
- مجموعه همه زبانهای نامنظم روی یک الفبا، یک مجموعه شمارای نامتناهی است.
- مجموعه همه ماشینهای تورینگ روی یک الفبا، یک مجموعه شمارای نامتناهی است.
- هر زبان نامتناهی تشخیصپذیر تورینگ، یک زیرمجموعه نامتناهی تصمیمپذیر دارد.
بررسی گزاره 1: هر زبانی که RE نباشد قطعا REC هم نیست زیرا زبانهای REC زیر مجموعه زبانهای RE هستند. پس این گزاره درست است.
بررسی گزاره 2: کل زبانهای قابل تعریف روی الفبا ناشمارا و زبانهای منظم شمارا هستند. حال میدانیم که اگر یک مجموعه شمارا را از یک مجموعه ناشمارا کم کنیم، مجموعه حاصل همچنان ناشمارا خواهد بود. اگر از مجموعه کل زبانها، مجموعه زبانهای منظم را کم کنیم، مجموعه حاصل شامل کلیه زبانهای نامنظم است که ناشمارا نیز هست. در نتیجه این گزاره نادرست است.
بررسی گزاره 3: در درس نظریه زبانها میدانیم که مجموعه همه ماشینهای تورینگ روی الفبا شمارا هستند پس این گزاره درست است.
بررسی گزاره 4: از برهان خلف استفاده میکنیم. یعنی فرض میکنیم هر زبان منظم، زیر مجموعه نامتناهی ندارد اما ما میدانیم که زبانهای منظم خود هم زبان REC و هم زبان RE است. پس امکان ندارد زبان منظم نامتناهی که RE است، همه زیر مجموعههایش فقط RE بوده و REC نیست. در نتیجه این گزاره صحیح است.
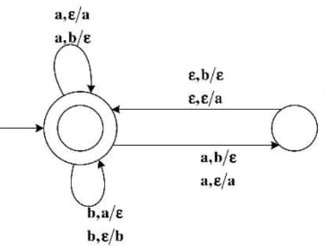
برای تولید زبان بالا گرامر زیر پیشنهاد شده است. (S متغیر شروع و a تنها حرف الفبا است.)
$G: \;\;\; S\rightarrow [Ra]\; |\;a$
$\;\;\;\;\;\;\; Ra\rightarrow aaR$
$\;\;\;\;\;\;\;aL\rightarrow La$
$\;\;\;\;\;\;\;aH\rightarrow ?a $
$\;\;\;\;\;\;\;R]\rightarrow L]\; |\; H $
$\;\;\;\;\;\;\;[L\rightarrow [R $
$\;\;\;\;\;\;\;[?\rightarrow \varepsilon$
کدام گزینه در خصوص نوع گرامر بالا و عبارتی که بایستی به جای ? قرار گیرد، درست است؟
گرامر حساس به متن (نوع یک) به صورت افزایشی است یعنی $|LHS|\le |RHS|$ اما در گرامر داده شده وجود جمله $R]\to L$ (یا $R]\to H$) این قانون را نقض میکند در نتیجه گرامر بدون محدودیت است (حذف گزینههای 2 و 4) برای تشخیص علامت سوال بهتر است چند جملهی ابتدایی زبان را با استفاده از گرامر بسازیم.
$L=\left\{a,aa,aaaa,\dots \right\}$
ساخت رشته a:
$S\Rightarrow a$
ساخت رشته aa: در گام اول باید به صورت زیر عمل کنیم.
$S\Rightarrow [Ra]$
حال در این قسمت ما باید ببینیم ؟ چه میتواند باشد. اگر ؟ = R (بر اساس دو گزینه باقی مانده) باشد آنگاه شاید کسی بگوید که من بجای ساخت aa به صورت زیر عمل خواهم کرد.
$S\Rightarrow \left[Ra\right]{{\stackrel{[R\to \varepsilon }{\Longrightarrow}\ a]}}$
این در حالیست که [a عضو L نیست در نتیجه عبارت ؟ نباید برابر R باشد (حذف گزینه 3)
$S\rightarrow aSd|A|B$
$A\rightarrow aAd|C$
$B\rightarrow bBd|C$
$C\rightarrow bBCc|\varepsilon $
با استفاده از چندین مرحله اشتقاق، زبان گرامر داده شده را به صورت زیر محاسبه میکنیم.
\[S\ \Longrightarrow \left\{ \begin{array}{c} a^nBd^n\Longrightarrow \ a^nb^mCd^md^n\Longrightarrow a^nb^mb^rc^rd^md^n \\ a^nAd^n\Longrightarrow \ a^na^mCc^md^n\Longrightarrow a^na^mb^rc^rc^md^n \end{array} \longrightarrow a^nb^mc^rd^q\ |\ m+n=r+q\right.\]
پاسخ تشریحی سیگنال و سیستم کنکور ارشد کامپیوتر 1401
$y(t)+\frac {dy(t)}{dt}=x(t)\frac {dx(t)}{dt}$
بررسی خطی بودن: برای خطی بودن سیستم ابتدا خاصیت همگنی آن را چک میکنیم:
$T[ax(t)]=aT[x(t)]$
$T[ax(t)]=ax(t)\times a\frac {dx(t)}{dt}=a^2x(t)\frac {dx(t)}{dt}\neq aT[x(t)]=ax(t)\frac{dx(t)}{dt}$
در نتیجه سیستم داده شده غیرخطی است.
بررسی معکوس پذیری: شرط لازم برای معکوس پذیری یک سیگنال این است که ورودی همه لحظات در آرگومان x تولید شده و در ساخت خروجی نقش داشته باشند و همچنین همه ورودیها تولید شده و در ساخت خروجی نقش داشته باشند. در سیستم رو به رو اگر سیگنال ورودی دارای چندین نقطه اکسترمم باشد آنگاه در آن نقاط مشتق سیگنال ورودی برابر صفرشده و سیگنال ورودی در آن نقاط از روی خروجی قابل بازیابی نخواهد بود در نتیجه سیستم وارون ناپذیر است.
$\frac{dy(t)}{dt}+y(t) = \frac {dx(t)}{dt}$
اگر ورودی سیستم $x(t)=e^{-t}u(t)$ باشد، خروجی (t)y کدام است؟
از آنجایی که در صورت سوال گفته شده سیستم علی است پس:
$+\infty \in ROC[H(s)]$
حال چون سیستم پیوسته و LTI است میتوانیم با استفاده تبدیل لاپلاس و پاسخ ضربه سیستم، خروجی را با توجه به ورودی داده شده بیابیم:
$\frac{dy(t)}{dt}+y(t)=\frac {dx(t)}{dt}\Longrightarrow Y(s)(s+1)=sX(s)\Rightarrow H(s)=\frac {s}{s+1}$
$ROC[H(s)]={Re[s]>-1}\ or \ {Re[s] \lt -1}{\overset{+\infty \in ROC[H(s)]}{ \Longrightarrow}}ROC[H(s)]={Re[s]>-1}$
$x(t)=e^{-t}u(t)\Longrightarrow x(s)=\frac {1}{s+1}, Re[s]>-1$
$Y(s)= x(s) H(s)=\frac {s}{s+1}^2=\frac {A}{s+1}+\frac {B}{s+1}^2=\frac {1}{s+1}+\frac {-1}{(s+1)}^2 , Re[s]>-1$
$y(t) = \mathcal{L}^{- 1}\left\lbrack Y(s) \right\rbrack = e^{- t}u(t) - te^{- t}u(t)$
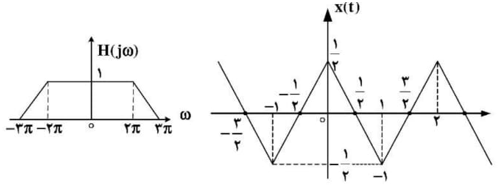
از آنجایی که سیگنال ورودی متناوب است، بهتر است از خواص سری فوریه برای حل این سوال استفاده کنیم. چون $x(t)$ با دورهی 2 متناوب است پس:
\[x(t) = \sum_ {- \infty}^{+ \infty}{z(t - 2k)},\ \ z(t) = \Lambda\left( \frac{t}{2 \times \frac{1}{2}} \right) - \frac{1}{2} \]
\[x(t) = \sum_ {- \infty}^{+ \infty}{z(t - 2k)}\overset{\text{ FS }}{\Rightarrow}\ a_{k} = \frac{1}{2}Z(\omega)|_{\omega = k\omega_{0}}\ \ ,\ \ \ (\omega_{0} = \frac{2\pi}{T} = \pi)\]
\[z(t) = \Lambda\left( \frac {t}{2 \times \frac{1}{2}} \right) - \frac{1}{2}\overset{\text{F}}{\Rightarrow}Z(\omega) = {4\left( \frac{\sin\frac{\omega}{2}}{\omega} \right)}^{2} - \pi\delta(\omega)\ \]
\[a_ {k} = {2\left( \frac{\sin\frac{\text{kπ}}{2}}{\text{kπ}} \right)}^{2} - \frac{\pi}{2}\delta\left( \text{kπ} \right) = \ \ {2\left( \frac{\sin\frac{\text{kπ}}{2}}{\text{kπ}} \right)}^{2} - \frac{1}{2} \delta(k)\]
چون سیستم LTI است پس:
\[x(t) = \sum_ {- \infty}^{+ \infty}{a_{k}e^{\text{jk}\omega_{0}t}} \Longrightarrow y(t) = \sum_{- \infty}^{+ \infty}{a_{k}H\left( k\omega_{0} \right)e^{\text{jk}\omega_{0}t}} = \sum_{- \infty}^{+ \infty}{a_{k}H\left( \text{kπ} \right)e^{\text{jkπt}}} \]
چون $H(K\pi )$ تنها در بازه $[-3,3\pi ]$ مقدار دارد پس:
\[y(t) = \sum_ {- \infty}^{+ \infty}{a_{k}H\left( \text{kπ} \right)e^{\text{jkπt}}} = \sum_{- 2}^{+ 2}{a_{k}H\left( \text{kπ} \right)e^{\text{jkπt}}}\]
حال باید ضرایب سری فوریه سیگنال خروجی را محاسبه کنیم:
\[a_ {k} = {2\left( \frac{\sin\frac{\text{kπ}}{2}}{\text{kπ}} \right)}^{2} - \ \frac{\pi}{2}\delta\left( \text{kπ} \right)\ \Longrightarrow \ \left\{ \begin{matrix} a_{- 1} = \frac{2}{\pi^{2}} \\ a_{- 2}\ ,a_{2} = \ 0 \\ a_{1} = \frac{2}{\pi^{2}} \\ \end{matrix} \right.\ a_{0} = \frac{1}{2}\int_{- 1}^{1}{x(t)\text{dt}}= 0\]
اکنون که مقادیر $a_k$ بدست آمده میتوانیم خروجی را در نقاط خواسته شده بیابیم:
\[y(0) = \sum_ {- 2}^{+ 2}{a_{k}H\left( \text{kπ} \right)} = \underset{0}{\overset{a_{- 2}H( - 2\pi)}{︸}} + a_{- 1}\underset{1}{\overset{H( - \pi)}{︸}} + \underset{0}{\overset{a_{0}}{︸}} + a_{1}\underset{1}{\overset{H(\pi)}{︸}} + \underset{0}{\overset{a_{2}H(2\pi)}{︸}}\ = \ \frac{2}{\pi^{2}}\ + \ \frac{2}{\pi^{2}}\ = \ \frac{4}{\pi^{2}} \]
\[y\left( \frac {1}{2} \right) = \sum_{- 2}^{+ 2}{a_{k}H\left( \text{kπ} \right)e^{\text{jk}\frac{\pi}{2}}} = a_{- 1}e^{- j\frac{\pi}{2}} + a_{1}e^{j\frac{\pi}{2}} = - j\frac{2}{\pi^{2}} + j\frac{2}{\pi^{2}} = 0\]
\[y(0)\ + \ y\left( \frac {1}{2} \right) = \ \frac{4}{\pi^{2}} \]
$H(e^{j\omega})=\frac {4}{5-4cos(\omega)}$
اگر ورودی این سیستم (n)x به صورت شکل زیر باشد و خروجی آن (n)y باشد، مقدار $\sum\limits_{k=0 }^{+\infty }y(k)$ کدام است؟
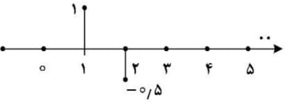
میدانیم که :
$\alpha ^{|n|},|\alpha |<1{\overset{F}{\Longrightarrow }}\frac {1-\alpha ^2}{1-2\alpha \;cos\;\omega +\alpha ^2}$
حال اگر$\alpha=\frac {1}{2}$ باشد:
$(\frac {1}{2})^{|n|},|\frac {1}{2}| \lt 1 {\overset{F}{\Longrightarrow }}\frac {\frac {3}{4}}{\frac{5}{4}-cos\;\omega} $
$\frac {4}{3}(\frac {1}{2})^{|n|},|\frac {1}{2}| \lt 1 {\overset{F}{\Longrightarrow }}H(e^{j\omega} )=\frac {1}{\frac{5}{4}-cos\;\omega} $
با توجه به نمودار داده شده برای سیگنال ورودی، میتوان گفت که:
$x[n]=\delta [n-1]-\frac {1}{2}\delta [n-2]$
$y[n]=x[n]*h[n]=(\delta [n_1]-\frac {1}{2}\delta [n-2]*h[n]=h[n_1]-\frac {1}{2}h[n_2]$
در نتیجه برای محاسبه خواستهی مساله داریم:
\[\sum_ {n = 0}^{+ \infty}{y\lbrack n\rbrack = \sum_{n = 0}^{+ \infty}\left( h\lbrack n - 1\rbrack - \frac{1}{2}h\lbrack n - 2\rbrack \right)} = \sum_{n = 0}^{+ \infty}{h\lbrack n - 1\rbrack}\ - \ \frac{1}{2}\sum_{n = 0}^{+ \infty}{h\lbrack n - 1\rbrack} \]
\[\sum_ {n = 0}^{+ \infty}{y\lbrack n\rbrack} = \ \sum_{n = 0}^{+ \infty}{\frac{4}{3}\left( \frac{1}{2} \right)^{|n\ - \ 1|}} - \ \frac{1}{2}\sum_{n = 0}^{+ \infty}{\frac{4}{3}\left( \frac{1}{2} \right)^{|n\ - \ 2|}} \]
\[\sum_ {n = 0}^{+ \infty}{\frac{4}{3}\left( \frac{1}{2} \right)^{|n\ - \ 1|}} = \frac{4}{3}\left\lbrack \frac{1}{2} + 1 + \left( \frac{1}{2} \right) + \left( \frac{1}{2} \right)^{2} + \ldots \right\rbrack\ = \ \frac{4}{3}\left\lbrack \frac{1}{2} + \frac{1}{1\ - \ \frac{1}{2}} \right\rbrack = \frac{10}{3} \]
\[\frac {1}{2}\sum_{n = 0}^{+ \infty}{\frac{4}{3}\left( \frac{1}{2} \right)^{|n\ - \ 2|}} = \ \frac{2}{3}\left\lbrack \left( \frac{1}{2} \right)^{2} + \left( \frac{1}{2} \right) + 1 + \left( \frac{1}{2} \right) + \left( \frac{1}{2} \right)^{2} + \ldots \right\rbrack = \ \frac{2}{3}\left\lbrack \left( \frac{1}{2} \right)^{2} + \left( \frac{1}{2} \right) + \frac{1}{1\ - \ \frac{1}{2}} \right\rbrack = \frac{11}{6} \]
\[\sum_ {n = 0}^{+ \infty}{y\lbrack n\rbrack} = \ \sum_{n = 0}^{+ \infty}{\frac{4}{3}\left( \frac{1}{2} \right)^{|n\ - \ 1|}} - \ \frac{1}{2}\sum_{n = 0}^{+ \infty}{\frac{4}{3}\left( \frac{1}{2} \right)^{|n\ - \ 2|}} = \ \frac{10}{3}\ - \ \frac{11}{6}\ = \ \frac{9}{6} = \frac{3}{2}\]
میدانیم که:
$(n+1)u[n]{\overset{z}{\Longrightarrow }}\frac {1}{(1-z^{-1})^2}$
$u[n]{\overset{z}{\Longrightarrow }}\frac {1}{(1-z^1)}$
با کم کردن طرفین دو عبارت بالا به این تبدیل Z خواهیم رسید:
$(n+1)u[n]-u[n]=nu[n]{\overset{z}{\Longrightarrow }}\frac {1}{(1-z^{-1})^2}-\frac {1}{1-z^{-1}}=\frac {z^{-1}}{(1-z^{-1})^2},|z|>1$
حال که تبدیل Z سیگنال ورودی را محاسبه کردیم، خروجی به صورت زیر خواهد شد:
$Y(z)=X(z)H(z)=\frac {z^{-1}}{(1-z^{-1})^2(1-\frac {1}{2}z^{-1})}=\frac {A}{1-z^{-1}}\frac {B}{(1-z^{-1})}^2+\frac {C}{(1-\frac {1}{2}z^{-1})}$
با توجه به خاصیت تفکیک کسرها، ضرایب را محاسبه میکنیم:
$Y(z)=X(z)H(z)=\frac {z^{-1}}{(1-z^{-1})^2(1-\frac {1}{2}z^{-1})}=\frac {-4}{1-z^{-1}}\frac {2}{(1-z^{-1})}^2+\frac {2}{(1-\frac {1}{2}z^{-1})},|z|>1$
$y[n]=z^{-1}[y(z)]=-4u[n]+2(n+1)u[n]+2(\frac{1}{2})^n u[n]$
$\lim_{n\to \infty }\frac {y[n]}{n}=\lim_{n\to \infty }\frac {-4u[n]+(n+1)u[n]+2(\frac {1}{2}) ^n U[n]}{n}=2$
دروس تخصصی 2 (ساختمان دادهها، طراحی الگوریتم و هوش مصنوعی):
پاسخ تشریحی ساختمان داده و الگوریتم کنکور ارشد کامپیوتر 1401
![]()
که در آن $\delta(u, v)$ برابر با طول کوتاهترین مسیر جهتدار از u به v در گراف G است. در چه مرتبه زمانی میتوان مقادير $d(u,S)$ را به ازای تمام رأسهای u از گراف محاسبه کرد؟ دقت کنید که خروجی شامل n مقدار به ازای تمام رأسهای u از گراف است. (بهترین گزینه را انتخاب کنید.)
همانطور که به خاطر دارید در گراف مسطح شرط $e<3n-6$ برقرار است یعنی مطمئنیم که گراف ما خلوت بوده یا $e\ \epsilon\ \theta\left(n\right)$ حال برای حل این سوال اگر به الگوریتمهای کلاسیک فکر کنیم. مرتبه کراسال $\theta\left(n\log{n}+n+n\alpha\right)$ و مرتبه پریم $\theta(n+\ n\ log\ n)$ خواهد بود که برای گراف خلوت ما مرتبهی بالایی هستند و باید بتوان در مرتبه کمتری این کار را انجام داد. نکته) اگر یالها در الگوریتم کراسال از قبل مرتب باشند مرتبه برابر $\mathbf{\theta}\left(\mathbf{n}+e\mathbf{\alpha}\right)$ میشود. اگر به خاطر داشته باشید در یکی از مراحل الگوریتم کراسال نیاز به مرتب کردن یالها بود که مرتبهی O(e\log{e}) ناشی از این مرتب سازی بود. حال این مرتبسازی در صورت استفاده از الگوریتمهایی مانند مرتب سازی ادغامی یا مرتب سازی سریع پدید میآمد. حال با توجه به اینکه گراف ما خلوت بوده یا $e\ \epsilon\ \theta\left(n\right)$ میتوان استفاده از الگوریتمهای دیگر مرتب سازی مثل مانند مرتب سازی شمارشی پیدا کردن درخت پوشای کمینه در مرتبه کمتری انجام داد.
برای این کار به صورت زیر عمل میکنیم:
- ابتدا سنگین ترین یال را پیدا میکنیم (مرتبهی پیدا کردن kامین بزرگترین عضو برابر با $\theta\left(n\right)$ است)
- حال با استفاده از مرتب سازی شمارشی یالها را مرتب میکنیم:
دقت کنید که مرتبه مرتب سازی شمارشی برابر با $O\left(n+k\right)$ است که k بزرگترین عدد ما است. این مرتبه به k یعنی وزن بزرگترین یال ما وابسته است و اگر مقدار این یال ثابت نباشد (مثلا $k=n^2)$ ممکن است مرتبه الگوریتم بیشتر از حد ذکر شده بشود ولی فعلا برای سادگی و برای این الگوریتم فرض میکنیم مقدار یالها ثبات است و مرتبه مرتب سازی برابر با $O\left(n\right)$ میباشد. - حال ادامهی الگوریتم کراسال را در مرتبه $O\left(n\right)$ انجام میدهیم ( ادامهی این الگوریتم ساخت n تا مجموعهی تک عضوی با رئوس و انتخاب یالها به ترتیب است.
مشخص است که مرتبهی الگوریتم مطرح شده در بالا برابر با عبارت زیر میباشد.
$O\left(n\right)+O\left(n\right)+O\left(n\right)=O\left(n\right)$
حال همانطور که گفته شد مرتبه مرتب سازی شمارشی به وزن بیشترین یال نیز وابسته خواهد بود و اگر بخواهیم الگوریتمی مطرح کنیم که نیاز به فرضی برای این یال نیز نداشته باشیم باید از الگوریتم بروکا یا از الگوریتم Bernard Chazelle بهره بگیریم برای مطالعه این الگوریتمها میتوانید به لینکهای آنها مراجعه کنید. البته کتاب سی ال اس ار نیز روشی برای این کار ارائه کرده است در این لینک میتوانید آن را مطالعه کنید.
گرافی که بتوان آن را در صفحه جوری کشید که یالهایش همدیگر را قطع نکنند.
مثال) آیا $K_4$ مسطح است؟
$4=6-4+2$ (درست)
* تعداد نواحی را با $r$ نشان میدهند.
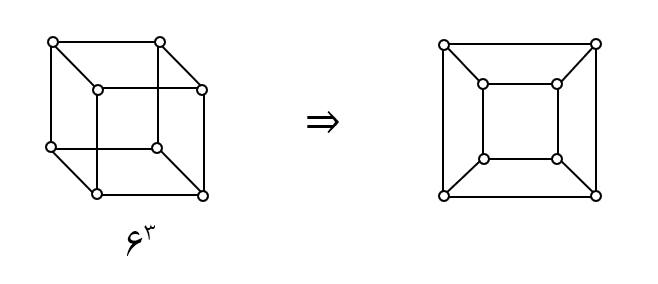
مثال) مکعب آیا مسطح است؟
$6=12-8+2$
* برای هر ناحیه درجه تعریف میشود و تعداد یالهای مرزی هرناحیه را درجه آن ناحیه میگویند.
قضیه) $r$ در گرافهای مسطح همبند از رابطه $r=e-n+2$ بدست میآید.
* در گراف مسطح $K$ مؤلفهای: $r=e-$
$6=12−10+3+1$ (درست)
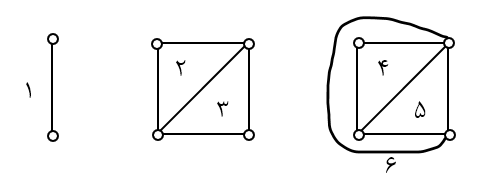
* برای نواحی درجه تعریف میکنند: تعداد یالهای مرزی هرناحیه را درجه آن ناحیه میگویند.
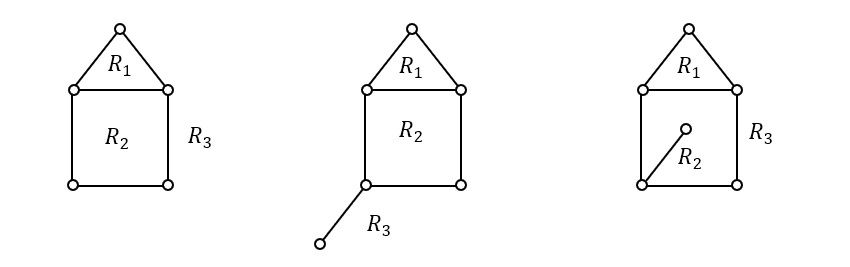 $\begin{matrix}\deg{\left(R_1\right)=3\ \ \ \ \ \ \ \ \ \ \ \ \ }&\ \ \ \ \ \ \ \ \ \ \ \ \deg{\left(R_1\right)=3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }&\ \ \ \ \ \ \ \ \ \deg{\left(R_1\right)=3}\\\deg{\left(R_2\right)=4\ \ \ \ \ \ \ \ \ \ \ \ \ }&\ \ \ \ \ \ \ \ \ \ \ \deg{\left(R_2\right)=4}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ &\ \ \ \ \ \ \ \ \ \ \deg{\left(R_2\right)=6}\\\deg{\left(R_3\right)=5}\ \ \ \ \ \ \ \ \ \ \ \ \ &\ \ \ \ \ \ \ \ \ \ \ \ \deg{\left(R_3\right)=7}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ &\ \ \ \ \ \ \ \ \ \ \deg{\left(R_3\right)=5}\\\end{matrix}$
$\begin{matrix}\deg{\left(R_1\right)=3\ \ \ \ \ \ \ \ \ \ \ \ \ }&\ \ \ \ \ \ \ \ \ \ \ \ \deg{\left(R_1\right)=3\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }&\ \ \ \ \ \ \ \ \ \deg{\left(R_1\right)=3}\\\deg{\left(R_2\right)=4\ \ \ \ \ \ \ \ \ \ \ \ \ }&\ \ \ \ \ \ \ \ \ \ \ \deg{\left(R_2\right)=4}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ &\ \ \ \ \ \ \ \ \ \ \deg{\left(R_2\right)=6}\\\deg{\left(R_3\right)=5}\ \ \ \ \ \ \ \ \ \ \ \ \ &\ \ \ \ \ \ \ \ \ \ \ \ \deg{\left(R_3\right)=7}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ &\ \ \ \ \ \ \ \ \ \ \deg{\left(R_3\right)=5}\\\end{matrix}$
نکته) $\sum {\mathrm{deg} \left(\text{نواحی}\right)\ }=2e$: چون هر یال مرز دو ناحیه است، هم داریم در این ناحیه میشماریم و هم در آن ناحیه
قضیه) در گراف همبند ساده مسطح که $n\geq3$ است آنگاه $e\le3n-6$
* گرافی حداقل 3 رأس دارد، درجه هر ناحیه آن حداقل 3 است. $\deg{\left(R_i\right)}\geq3$
${\mathrm{deg} \left(R_i\right)\ }\ge 3\Rightarrow \sum {\mathrm{deg} \left(R_i\right)\ }\ge 3r\to 2\text{e}\ge 3r\to 2\textrm{e}\ge 3\left(\text{e}-n+2\right)\Rightarrow 2\text{e}\ge 3\text{e}-3n+6 $
$\Rightarrow e\le3n-6$
توجه) اگر $e\le3n-6$ نبود میگوییم گراف مسطح نیست.
یاددآوری:
کراسال: یک الگوریتم حریصانه است که یالها را به صورت صعودی مرتب میکنیم و سپس هربار یال با کمترین وزن را انتخاب میکنیم بدون اینکه دور تشکیل شود، این کار را تا دیدن همهی رئوس ادامه میدادیم. (اینکار الگوریتم با استفاده از مجموعهها پیاده سازی شده است.)
نکته) مرتبه کراسال برابر $\mathbf{\theta}\left(e\mathbf{log}{e}+\mathbf{n}+e\mathbf{\alpha}\right)$ است. که $\mathbf{\alpha}$ ضریب آکرمن است.
نکته) اگر یالها از قبل مرتب باشند مرتبه برابر $\mathbf{\theta}\left(\mathbf{n}+e\mathbf{\alpha}\right)$ میشود.
پریم: یک الگوریتم حریصانه است، از راس گفته شده (یا دلخواه) شروع میکنیم و هربار راسی را ملاقات میکنیم که با راس شروع مجاور است و وزن یالش min است. و در ادامه هربار راسی را ملاقات میکنیم که با یکی از رئوس ملاقات شده مجاور باشد و دارای وزن یال min است.
نکته) پریم همیشه همبند جلو میرود ولی کراسال لزوما در مراحل میانی همبند نیست ولی قطعا در مرحله نهایی همبند است.
نکته) اگر وزنها یالهای گراف متفاوت باشد، درخت پوشا با هردو روش منحصر به فرد است. اما اگر وزن یکسان وجود داشته باشد ممکن است درختهای مختلفی ایجاد شود اما همیشه وزن درخت پوشای مینمم یکسان است.
نکته) مرتبه پریم
1- در صورت استفاده از ماتریس مجاورتی: $\theta(\mathbf{n}^\mathbf{2})$
2- در صورت استفاده از لیست مجاورتی
$\left\{\mathrm{\ \ \ } \begin{array}{c}\mathrm{binary\ minheap}\mathrm{\Rightarrow }\mathrm{T(n)}\mathrm{\in }\mathrm{\ }\mathrm{\theta }\mathrm{(e\ log\ n)} \\ \mathrm{fibonacci\ heap}\mathrm{\ }\mathrm{\Rightarrow }\mathrm{T(n)}\mathrm{\in }\mathrm{\ }\mathrm{\theta }\mathrm{(e+\ n\ log\ n)} \end{array}\right.$
نکته)
در لینکهای زیر نحوهی کار کردن الگوریتمهای کراسال و پریم را به صورت انیمیشن میتوانید ببینید.
پریم:
https://algorithms.discrete.ma.tum.de/graph-algorithms/mst-prim/
https://www.cs.usfca.edu/~galles/visualization/Prim.html
کراسال:
راه حل نامناسب:
به ترتیب از اول آرایه شروع کرده و عنصر اول را با خودش در شرط $A\left[1\right]\ast A\left[1\right]>1\ast 1$ چک میکنیم، سپس عنصر اول را با عنصر دوم در شرط $A\left[1\right]\ast A\left[2\right]>1\ast 2$ و... سپس عنصر اول با عنصر nام را در شرط $A\left[1\right]\ast A\left[n\right]>1\ast n$ چک میکنیم. حال فرایند گفته شده برای عنصر اول را دوباره برای عنصر دوم تا nام تکرار میکنیم.
مشخص است که مرتبه زمانی این الگوریتم $\theta\left(n^2\right)$ خواهد بود چون هرکدام از n عنصر با n عنصر دیگر چک شده.
راه حل مناسب:
- ابتدا فرمت شرط گفته شده را به $\frac{A\left[i\right]}{i}\ast\frac{A\left[j\right]}{j}>1$ تغییر میدهیم. دقت کنید که فرض کردهایم $i,j=1,2,\ldots,n$ که مشکلی پیش نیاید البته اگر صفر هم جز مقادیر قابل قبول در نظر میگرفتیم فقط کافی بود عنصر اول آرایه را کنار بگذاریم و برای آن بصورت جدا در مرتبهی $O\left(n\right)$ تعداد عناصری که شرط مارا صحیح میکنند محاسبه کنیم. حال برای تمامی عناصر مقدار $\frac{A\left[i\right]}{i}$ را محاسبه کرده و در همان خانه جایگزین میکنیم (البته میتوانیم از آرایه دیگری مانند B نیز استفاده کنیم ولی در مرتبه زمانی اثری ندارد) این کار مرتبه $O\left(n\right)$ خواهد داشت.
- آرایه بدست آمده را مرتب میکنیم $O\left(n\log{n}\right)$
- حال در این آرایه کافیست عناصری که شرط $B\left[i\right]\ast B\left[j\right]>1$ را برقرار میکند پیدا کنیم. برای اینکار از ایدهی جستوجوی دودویی کمک میگیریم. مشخص است که هرجا برای عنصر $B\left[i\right]$ عنصر $B\left[j\right]$ ای پیدا کنیم که $B\left[i\right]\ast B\left[j\right]>1$ مطمئن خواهیم بود که برای $j=j,j+1,\ldots,n$ شرط $B\left[i\right]\ast B\left[k\right]>1$ برقرار خواهد بود پس به صورت زیر عمل میکنیم: حال روند الگوریتم به این صورت خواهد بود که ابتدا عنصر $ j=\frac{n}{2}$ را چک میکنیم که دو حالت پیش میآید:
حال روند الگوریتم به این صورت خواهد بود که ابتدا عنصر $j=\frac{n}{2}$ را چک میکنیم که دو حالت پیش میآید:
- اگر شرط $B\left[i\right]\ast B\left[j\right]>1$ برقرار باشد. میفهمیم که عناصر سمت راست همه شرط $B\left[i\right]\ast B\left[j\right]>1$ را برقرار میسازند. پس $j=\frac{j}{2}$ قرار داده و سمت چپ آرایه را چک میکنیم.
- اگر شرط $B\left[i\right]\ast B\left[j\right]<1$ برقرار باشد. میفهمیم که عناصر سمت راست لزوما همه شرط $B\left[i\right]\ast B\left[j\right]>1$ را برقرار نمیسازند و باید در سمت راست تا جایی پیش برویم که عنصری شرط را برقرا کند پس $j=\frac{3j}{2}$ قرار داده و سمت راست آرایه را چک میکنیم.
این کار را تا جایی ادامه میدهیم که آخرین عنصر شرط $B\left[i\right]\ast B\left[j\right]>1$ برقرار نسازد و تمام عناصر در سمت راست آن تعداد جفت اندیسها خواهد بود.
مشخص است که مرتبه الگوریتم مطرح شده در قدم سوم $O\left(\log{n}\right)$ خواهد بود. حال چون برای تمام عناصر باید اولین عنصری که شرط $B\left[i\right]\ast B\left[j\right]>1$ برقرار میسازد پیدا کنیم، پس n بار این کار را تکرار کرده پس و این مرحله $O\left(n\log{n}\right)$ خواهد بود.
با توجه به الگوریتم مطرح شده مرتبه این کار برابر خواهد بود با:
$O\left(n\log{n}\right)+O\left(n\right)+O\left(n\log{n}\right)=O\left(n\log{n}\right)$
موارد اضافی:
سوال: با توجه به آرایه A قصد داریم تعداد جفتهایی پیدا کنیم که $A[i]>A[j]$ است بطوری که $i<j$ است را چاپ کنیم مرتبه انجام این کار چقدر است:
راه حل نامناسب:
به ترتیب از اول آرایه شروع کرده و عنصر اول را با خودش در شرط $A[1]>A[1]$ چک میکنیم، سپس عنصر اول را با عنصر دوم در شرط $A[1]>A[2]$ و... سپس عنصر اول با عنصر nام را در شرط $A[1]>A[n]$ چک میکنیم. حال فرایند گفته شده برای عنصر اول را دوباره برای عنصر دوم تا nام تکرار میکنیم. مشخص است که مرتبه زمانی این الگوریتم $\theta\left(n^2\right)$ خواهد بود چون هرکدام از n عنصر با n عنصر دیگر چک شده.
راه حل مناسب:
شرط مطرح شده در صورت سوال همان مساله شمردن تعداد وارونگی یا $Inversion$ در آرایه میباشد که با استفاده از مرتب سازی ادغامی در مرتبهی $O\left(n\log{n}\right)$ میتوان تعداد آن را محاسبه کرد.
وارونگی نسبت به صعودی بودن:
وقتی یک آرایه داریم و برای دو عنصر $A[i],A[j]$ با جایگاه (اندیس) به ترتیب $i,j$ شرط زیر برقرار است میگوییم که یک وارونگی (زوج- معکوس بر اساس این تست یا $inversion$) داریم.
$j>i\ but\ A[i]>A[j]$
برای پیدا کردن وارونگیها از سمت چپ به راست، حرکت میکنیم تمامی عناصری که از یک عنصر کوچکتر هستند با آن عنصر وارونه هستند.
مثال) آرایه زیر چند وارونگی دارد:
$A\left[1\ldots5\right]=\left[12\ 4\ 9\ 7\ 5\right]$
وارونگی ها:
$\left(12,4\right)\left(12,9\right)\left(12,7\right)\left(12,5\right)$
$\left(9,7\right)\left(9,5\right)$
$\left(7,5\right)$
در کل 7 وارونگی داریم.
نکته) آرایه صعودی وارونگی ندارد.
نکته) آرایه نزولی max تعداد وارونگی دارد.
راه اثبات 1) چون هر عنصر با تمامی عناصر بعدش وارونگی دارد پس تعداد وارونگی آرایه نزولی برابر است با
$\underbrace{\mathrm{n-1}}_{\text{تعداد عناصر بعد از عنصر اول}}\mathrm{+}\underbrace{\mathrm{n-2}}_{\text{تعداد عناصر بعد از عنصر اول}}\mathrm{+}\mathrm{\cdots }\mathrm{+1+}\underbrace{0}_{\text{عنصر آخر}}\mathrm{=}\frac{\mathrm{n}\left(\mathrm{n-1}\right)}{\mathrm{2}}$
دقت کنید تعداد وارونگیها را دوبار نشمارید برای مثال عنصر آخر با تمامی عناصر قبل از خودش وارونگی دارد اما چون در محاسبه $n-1$ قبلی این وارونگیها به حساب آوردهایم نباید $n-1$ وارونگی هم برای عنصر آخر جمع کنیم.
راه اثبات 2) هر دو عنصری که انتخاب کنیم چون آرایه نزولی است قطعا شرط $j>i\ but\ A[i]>A[j]$ برقرار است پس تعداد وراونگی برابر تعداد انتخاب بدون ترتیب دو عنصر از n عنصر است.
$n2=n(n-1)2$
موارد گفته شده را در آرایه نزولی زیر میتوانید امتحان کنید.
$A\left[1\ldots4\right]=\left[12\ 8\ 5\ 3\ 1\right]$
نکته) متوسط تعداد وارونگیها در یک آرایه برابر با $\frac{n(n-1)}{4}$ است.
اثبات:
روش 1: فرض کنید $L$ یک لیست دلخواه از عناصر است و $L_R$ لیستی با عناصر L است که بصورت برعکس چیده شده است برای مثال:
$L=\left[b\ e\ f\ a\ g\right]\ ,\ L_R=[g\ a\ f\ e\ b]$
حالا دو عضو از لیست $L$ انتخاب میکنیم، برای این کار $\left( \begin{array}{c}\mathrm{n} \\ \mathrm{2} \end{array}\right)$ حالت وجود دارد. دو عضوی که انتخاب کردیم در حداقل یکی از لیستهای $L$ یا $L_R$ با یکدیگر وارونگی دارند. بنابراین میتوان نتیجه گرفت در دو لیست $L$ و $L_R$ در مجموع $\left( \begin{array}{c}\mathrm{n} \\ \mathrm{2} \end{array}\right)$ وارونگی وجود دارد.
حال برای اعضای هر لیستی n! جایگشت وجود دارد که این تعداد جایگشت را به دو مجموعهی مجزا که یکی شامل $L$ها و دیگری شامل $L_R$ ها است تقسیم میکنیم (به عبارت دیگر نصفی از جایشگتها برعکس شدهی نصفه ی دیگر هستند). در نتیجه میتوان فهمید که میانگین وارونگیها در کل جایشگتهای برابر است با $\frac{\frac{n(n-1)}{2}}{2}=\frac{n(n-1)}{4}$.
روش 2 (استقرا): در استقرا ابتدا برای تعدادی عدد کوچک درستی قضیه $P(n)$ را چک میکردیم و سپس قضیه را برای $P(k)$ درست فرض میکردیم و برای $P(k+1)$ درستی آن را اثبات میکردیم. برای قضیه "تعداد میانگین وارونگی برابر است با $\frac{n(n-1)}{4}$ " ابتدا برای آرایهای با $n=1$ آن را چک میکنیم سپس برای $P(K)$ ان را اثبات میکنیم. (اثبات کامل را در این لینک میتوانید مطالعه کنید)
نکته) زمان اجرا الگوریتم مرتب سازی درجی مستقیماً به تعداد وارونگیها بستگی دارد و اگر آرایه I وارونگی داشته باشد زمان اجرای مرتب سازی درجی برابر $\theta\left(n+I\right)$ است.
نکته) با مرتب سازی درجی و ادغامی میتوان تعداد وارونگیها شمرد.
نحوه شمردن مرتب سازی درجی:
در الگوریتم مرتب سازی درجی یک شمارنده اضافه میکنیم. هر جابهجایی که انجام شد یکی به شمارنده اضافه میکنیم به معنی اینکه هر این جابهجایی به دلیل یک وارونگی بوده که به وسیله الگوریتم حل شده.
یاددآوری: در مرتب سازی درجی هربار از عنصر دوم شروع میکنیم هر عنصر را در انتهای آرایه درج میکنیم با عناصر قبلی مقایسه میکنیم اگر جایشان درست نبود باید جابهجایی انجام میدادیم برای مثال:
$A\left[1\ldots5\right]=\left[12\ 4\ 9\ 7\ 5\right]$
ابتدا 4 را درج میکنیم پس جایش باید با 12 تغییر کند. $[4\ 12]$
سپس 9 را درج میکنیم و دوباره 9 جایش را با 12 تغییر میدهد. $[4\ 9\ 12\ \ ]$
7 را درج میکنیم به ترتیب جایش با 12 و 9 تغییر میدهد. $[4\ 7\ 9\ 12]$
5 را درج میکنیم جایش را با 12، 9 و 7 تغییر میدهد. $[4\ 5\ 7\ 9\ 12]$
در مجموع 7 جابهجایی و در نتیجه 7 وارونگی داشتیم.
نحو شمردن مرتب سازی ادغامی:
در این الگوریتم نیز یک کانتر میگذاریم. و هر وقت کسی از لیست y انتخاب شد کانتر را با تعداد تمامی عناصر موجود در لیست x جمع میزنیم و این کار را در تمامی مراحل مرتب سازی ادغامی انجام میدهیم. (از مقایسه آرایههای کوچک شده و تک عنصری تا آخرین مرحله.)
سوال: با توجه به آرایه A که عناصر آن اعداد طبیعی هستند قصد داریم تعداد جفتهایی پیدا کنیم که $A[i]*A[j]=A[i]+A[j]$ است را چاپ کنیم مرتبه انجام این کار چقدر است:
راه حل نامناسب: به ترتیب از اول آرایه شروع کرده و عنصر اول را با خودش در شرط $A[1]*A[1]=A[1]+A[1]$ چک میکنیم، سپس عنصر اول را با عنصر دوم در شرط $A[1]*A[2]=A[1]+A[2]$ و... سپس عنصر اول با عنصر nام را در شرط $A[1]*A[n]=A[1]+A[n]$ چک میکنیم. حال فرایند گفته شده برای عنصر اول را دوباره برای عنصر دوم تا nام تکرار میکنیم. مشخص است که مرتبه زمانی این الگوریتم $\theta\left(n^2\right)$ خواهد بود چون هرکدام از n عنصر با n عنصر دیگر چک شده.
راه حل مناسب: شرط مطرح شده را به صورت زیر بازنویسی میکنیم:
\[\mathrm{A[i]*A[j]=A[i]+A[j]}\mathrm{\Rightarrow }\mathrm{A[i]*A[j]-A[i]-A[j]=0}{{\stackrel{\mathrm{+1}}{\Longrightarrow}}}\mathrm{A[i]*A[j]-A[i]-A[j]+1=1}\mathrm{\Rightarrow }\mathrm{A[i](A[j]-1)-(A[j]-1)=1}\mathrm{\Rightarrow }\mathrm{(A[i]-1)*(A[j]-1)=1}\]
حال برای اینکه شرط بالا اتفاق بیفتید با توجه به طبیعی بودن اعضای A یا باید هردو $A[i]$ و $A[j]$ برابر با 2 باشند یا هردو باید برابر با صفر باشند.
برای همین کافیست تعداد 2ها و 0های آرایهی A را بشماریم که با یک پیمایش این آرایه در مرتبهی $O(n)$ قابل انجام است
کافیست هیپ گفته شده را رسم نماییم ابتدا باید مشخص کنیم که برگها در کدام سطح شروع میشوند، میتوانید از فرمول نیز برای این کار استفاده کنید اما به راحتی میدانیم که در سطح اول 1 راس در سطح دوم 2 راس در سطح سوم 4 راس در سطح چهارم 8 راس در سطح پنجم 16 راس در سطح ششم 32 راس و در سطح هفتم 64 راس وجود دارد که $1+2+4+8+16+32+\ 64=127$ پس درختی داریم که همهی برگهای آن همسطح بوده و در سطح هفتم قرار دارند حال کافیست این درخت را جوری رسم کنیم که بیشترین تعداد عناصر بالای 100 در برگها قرار بگیرند، بدین منظور چون درخت ما یک هرم بشینه است مجبوریم عناصر را از بزرگ به کوچک جوری بچینیم که در کمترین تعداد مصرف عناصر به برگها برسیم بدین منظور دائم به سمت چپ حرکت کرده و عناصر را از بزرگ به کوچک میچنیم، وقتی به برگ رسیدیم یک سطح (یا اگر لازم بود بیشتر) به بالا برگشته و دوباره با کمترین تعداد عناصر سعی میکنیم به برگ برسیم برای مثال مسیر قرمز مشخص شده در شکل زیر نشان دهندهی این روند است.
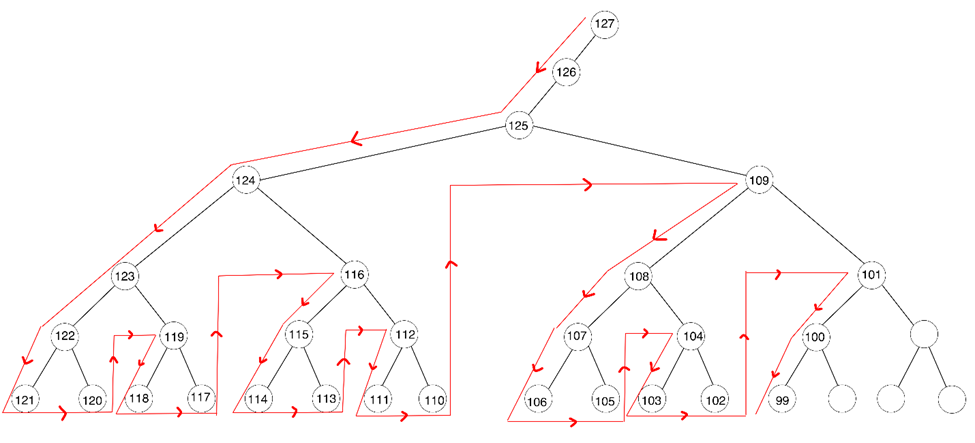
با شمردن راسهای بیشتر از 100 در برگها متوجه میشویم که در بهترین حالت 12 عنصرمیتواند در آنها واقع شود.
یاددآوری:
max tree: داخل هر نود عددی است و آن عدد بزرگتر مساوی فرزندانش است.
Maxheap یا هرم ماکسیمم: درختی max tree و کامل است پس تمام خواص درخت کامل را دارد (پر بودن تا سطح یکی مانده به آخر و هر سطح برگها از چپ به راست قرار داده میشوند). به عبارت دیگر هرم بشینه یک درخت کامل است که هر نود از فرزندارن خودش بزرگتر است. Maxheap را میتوان با آرایه یا لیست پیوندی نشان داد ولی با توجه به کامل بودنش معمولا از آرایه استفاده میکنند.
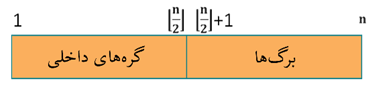
همانطور که مشخص است در هیپ $[n/2]$ عنصر اول گرههای داخلی و $[n/2]$ عنصر دوم برگها هستند.
نکته) maxheap که خاصیت BST دارد درخت مورب چپ است.
ماکس اول در ریشه است. $A[1]$
ماکس دوم در سطح دوم قرار دارد. $A[2..3]$
ماکس سوم در سطح دوم یا سطح سوم قرار دارد. $A[2…7]$
ماکس r در سطح دوم یا سوم یا.... r قرار دارد. بنابراین داریم:
$\mathbf{A}[\mathbf{2},\ldots.,\mathbf{2}^\mathbf{r}-\mathbf{1}]$
میتواند قرار بگیرد.
نکته) با توجه به نکته ی بالا میتوان فهمید که مینمم از سطح دو تا آخرین سطح میتواند قرار بگیرد ولی باید دقت داشت که مینمم همیشه در برگها است.
نکته) هرم برای جستوجو مناسب نیست و مرتبهی جستوجو در هرم $O(n)$ است.
نکته) بهترین روش ساخت هرم کامل از مرتبه n است.
نکته) مرتبه درج و حذف در هرم از مرتبه $O(log \ n)$ است.
راه حل: کافیست روند رشد توابع را بررسی کنیم:
$\log{n},\ \log^2{n},\ \log{n^2},n\log^2{n},\ \log{n!}\ ,\ \log{n^n}$
حال بعضی از توابع را برای ساده سازی به صورتهای زیر بازنویسی میکنیم:
$\log^2{n}=\log{n}\ \ast\ \log{n}$
$\log{n^2}=2\log{n}$
$n\log^2{n}=nlog{n}\ \ast\ \log{n}$
$\log{n!}\epsilon\ \theta\ \left(n\log{n}\right)$
$\log{n^n}=n\log{n}$
دقت کنید که عبارت $\log{n!}=\left(n\log{n}\right)$ نادرست است، این دو تابع هم رشد هستند اما مساوی نیستند. حال با توجه به عبارات بالا کافیست به روند صعودی توابع را بازنویسی کنیم
مشخص است که $\log{n}\epsilon\ O(\log^2{n})$ که میتوان با استفاده از خواص مجانبی نیز اثبات کرد.
${\mathop{\mathrm{lim}}_{\mathrm{n}\mathrm{\to }\mathrm{\infty }} \frac{{{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }}{{\mathrm{log} \mathrm{n}\ }}\ }\mathrm{=}\frac{{\mathrm{log} \mathrm{n}\ }\mathrm{\ *\ }{\mathrm{log} \mathrm{n}\ }}{{\mathrm{log} \mathrm{n}\ }}\mathrm{=}{\mathrm{log} \mathrm{n}\ }\mathrm{=}\mathrm{\infty }$
مشخص است که ${\mathrm{log} \mathrm{n}\ }\mathrm{\epsilon }\mathrm{\ }\mathrm{\theta }{\mathrm{(log} {\mathrm{n}}^{\mathrm{2}}\ }\mathrm{)}$ که میتوان با استفاده از خواص مجانبی نیز اثبات کرد
${\mathop{\mathrm{lim}}_{\mathrm{n}\mathrm{\to }\mathrm{\infty }} \frac{{\mathrm{log} {\mathrm{n}}^{\mathrm{2}}\ }}{{\mathrm{log} \mathrm{n}\ }}\ }\mathrm{=}\frac{\mathrm{2\ }{\mathrm{log} \mathrm{n}\ }}{{\mathrm{log} \mathrm{n}\ }}\mathrm{=}\mathrm{2}$
دقت کنید با اینکه دو تابع بالا دارای رشد برابر هستند به معنی برابر بودن مقادیر این توابع با n های مختلف نخواهد بود.
مشخص است که ${{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }\mathrm{\epsilon }\mathrm{\ O(n}{{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }\mathrm{)}$ که میتوان با استفاده از خواص مجانبی نیز اثبات کرد
${\mathop{\mathrm{lim}}_{\mathrm{n}\mathrm{\to }\mathrm{\infty }} \frac{{{\mathrm{nlog}}^{\mathrm{2}} \mathrm{n}\ }}{{{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }}\ }\mathrm{=}\mathrm{n}\mathrm{=}\mathrm{\infty }$
مشخص است که ${\mathrm{log} \mathrm{n!}\ }\mathrm{\epsilon }\mathrm{\ O(n}{{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }\mathrm{)}$ که میتوان با استفاده از خواص مجانبی نیز اثبات کرد.
${\mathop{\mathrm{lim}}_{\mathrm{n}\mathrm{\to }\mathrm{\infty }} \frac{{\mathrm{log} \mathrm{n!}\ }}{\mathrm{n}{{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }}\ }\mathrm{\le }{\mathop{\mathrm{lim}}_{\mathrm{n}\mathrm{\to }\mathrm{\infty }} \frac{{\mathrm{nlog} \mathrm{n}\ }}{\mathrm{n}{{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }}\ }\mathrm{=}{\mathop{\mathrm{lim}}_{\mathrm{n}\mathrm{\to }\mathrm{\infty }} \frac{\mathrm{1}}{{\mathrm{log} \mathrm{n}\ }}\ }\mathrm{=0}$
و همانطور که توضیح داده شد ${\mathrm{log} \mathrm{n!}\ }\mathrm{\epsilon }\mathrm{\ }\mathrm{\theta }\mathrm{\ }\left(\mathrm{n}{\mathrm{log} \mathrm{n}\ }\right)\mathrm{=}\mathrm{\theta }\mathrm{\ }\left({\mathrm{log} {\mathrm{n}}^{\mathrm{n}}\ }\right)$ حال توابع را به صورت صعودی مرتب میکنیم ( دقت کنید نحوهی نوشتن زیر فقط برای سادگی است و از لحاظ ریاضی صحیح نیست):
${\mathrm{log} \mathrm{n}\ }\mathrm{\le }{\mathrm{log} {\mathrm{n}}^{\mathrm{2}}\ }\mathrm{\le }\mathrm{\ }{{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }\mathrm{\le }\mathrm{\ }{\mathrm{log} {\mathrm{n}}^{\mathrm{n}}\ }\mathrm{\le }{\mathrm{log} \mathrm{n!}\ }\mathrm{\ \ }\mathrm{\le }\mathrm{\ n}{{\mathrm{log}}^{\mathrm{2}} \mathrm{n}\ }$
پس گزینهی 4 صحیح است.
یاددآوری:
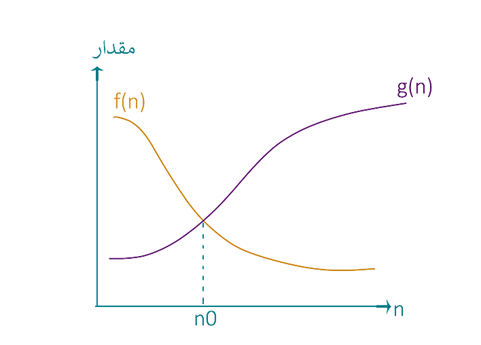
Big O: تابع $f(n)$ از مرتبه $O(g(n))$ است هرگاه رشد f کمتر مساوی رشد g باشد.
$\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{n}}\right)\boldsymbol{\mathrm{\in }}\boldsymbol{\mathrm{O}}\left(\boldsymbol{\mathrm{g}}\left(\boldsymbol{\mathrm{n}}\right)\right)\boldsymbol{\mathrm{\to }}\boldsymbol{\mathrm{\exists }}\boldsymbol{\mathrm{c}},{\boldsymbol{\mathrm{n}}}_{\boldsymbol{\mathrm{0}}}\boldsymbol{\mathrm{>}}\boldsymbol{\mathrm{0}}\boldsymbol{\mathrm{\ ,\ }}\boldsymbol{\mathrm{\forall }}\boldsymbol{\mathrm{\ }}\boldsymbol{\mathrm{n}}\boldsymbol{\mathrm{\ge }}\boldsymbol{\mathrm{\ }}{\boldsymbol{\mathrm{n}}}_{\boldsymbol{\mathrm{0}}}\boldsymbol{\mathrm{\ }}\boldsymbol{\mathrm{\Rightarrow }}\boldsymbol{\mathrm{\ }}\underbrace{\boldsymbol{\mathrm{0}}}_{\text{رشد برای توابع منفی معنی ندارد}}\boldsymbol{\mathrm{\le }}\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{n}}\right)\boldsymbol{\mathrm{\le }}\boldsymbol{\mathrm{c}}.\boldsymbol{\mathrm{g}}\boldsymbol{\mathrm{(}}\boldsymbol{\mathrm{n}}\boldsymbol{\mathrm{)}}$
O بزرگ کران بالا را مشخص میکند.
$\boldsymbol{\mathrm{O}}\left({\boldsymbol{\mathrm{n}}}^{\boldsymbol{\mathrm{2}}}\right)\boldsymbol{\mathrm{=}}\boldsymbol{\mathrm{\{}}\boldsymbol{\mathrm{\dots ,\ }}\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{n}}\right)\boldsymbol{\mathrm{,\ }}\frac{\boldsymbol{\mathrm{1}}}{\boldsymbol{\mathrm{n}}}\boldsymbol{\mathrm{,\ }}\boldsymbol{\mathrm{n}}\boldsymbol{\mathrm{\ ,\ }}\boldsymbol{\mathrm{n}}.\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{n}}\right)\boldsymbol{\mathrm{,\ }}\boldsymbol{\mathrm{3}}{\boldsymbol{\mathrm{n}}}^{\boldsymbol{\mathrm{2}}}\boldsymbol{\mathrm{+}}\boldsymbol{\mathrm{5}}\boldsymbol{\mathrm{,\ \dots .}}\boldsymbol{\mathrm{\}}}$
با توجه به خواص مجانبی میتوان عبارات زیر را نتیجه گرفت.
یاددآوری: میخواهیم نشان دهیم که $\log{n!}\in\theta\left(n\log{n}\right)$
نکته) $\log{a}\times b=\log{a}+\log{b}$
نشان دهیم $\log{n!}\in O\left(n\log{n}\right):$
$\log{n!}=\log{n}\times\left(n-1\right)\times\left(n-2\right)\times\ldots\times1=\log{n}+\log{n}-1+\ldots+\log{1}<\log{n}+\log{n}$
$+\ldots+\log{n}=n\log{n}\Rightarrow\log{n!}<n\log{n}\Rightarrow\log{n!}\in O\left(n\log{n}\right)$
نشان دهیم که $\log{n!}\in\mathrm{\Omega}\left(n\log{n}\right)$:
${\mathrm{log} n!\ }={\mathrm{log} n\ }\times n-1\times \dots \times {\mathrm{log} 1\ }={\mathrm{log} n\ }+{\mathrm{log} n\ }-1+\dots +{\mathrm{log} {n}/{2}\ }+\overbrace{{\mathrm{log} {n}/{2}\ }-1+\dots +}^{\text{اینها را کنار میگذاریم}}$${\mathrm{log} 1\ }>\underbrace{\mathrm{log}{\mathrm{n}}/{\mathrm{2}}\mathrm{+}{\mathrm{log} {\mathrm{n}}/{\mathrm{2}}\ }\mathrm{+\dots +}{\mathrm{log} {\mathrm{n}}/{\mathrm{2}}\ }}_{\text{است} \ {\mathrm{n}}/{\mathrm{2}}\text{ تعداد اینها}}\mathrm{=}{\mathrm{n}}/{\mathrm{2}}{\mathrm{log} {\mathrm{n}}/{\mathrm{2}}\ }\mathrm{=}{\mathrm{n}}/{\mathrm{2}}\left({\mathrm{log} \mathrm{n}\ }\mathrm{-}{\mathrm{log} \mathrm{2}\ }\right){n}/{2}\left({\mathrm{log} n\ }-1\right)$
$={n}/{2}{\mathrm{log} n\ }-{n}/{2}\Rightarrow {\mathrm{log} n!\ }>\underbrace{{n}/{2}{\mathrm{log} n\ }-{n}/{2}}_{=\in \theta \left(n{\mathrm{log} n\ }\right)}\Rightarrow {\mathrm{log} n!\ }\in \mathit{\Omega}\left(n{\mathrm{log} n\ }\right)$$(2)$
$(1),(2)$$\Rightarrow {\mathrm{log} n!\ }\in O\left(n{\mathrm{log} n\ }\right)\ |\ {\mathrm{log} n!\ }\in \mathit{\Omega}\left(n{\mathrm{log} n\ }\right)\to {\mathrm{log} n!\ }\in \theta \left(m{\mathrm{log} n\ }\right)$
روش 2 اثبات:
استرلینگ: $n!=\sqrt{2\pi n}\times\left(\frac{n}{e}\right)^n\left(1+\theta\left(\frac{1}{n}\right)\right)$
$\log{n!}=\frac{1}{2}\log{2\pi n}+n\log{\frac{n}{e}}+\log{\left(1+\theta\left(\frac{1}{n}\right)\right)}\Rightarrow\log{n!}\in\theta\left(n\log{n}\right)$
- محاسبه کوچکترین عدد
- محاسبه میانه
- تعیین آنکه آیا عدد داده شده xدر درخت وجود دارد.
- محاسبه مرتبه عدد x داده شده در بین n عدد ذخیره شده در درخت
درخت جستوجوی دودویی معرفی شده دارای ارتفاع $O(log\ n)$ میباشد پس تمام عملیات حذف، درج، جستوجو در این درخت در مرتبهی $O(log\ n)$ انجام میشود.
حال باید تک تک عبارات گفته شده را بررسی کنیم:
- محاسبه کوچکترین عدد: مشخص است که در درخت جستوجوی دودویی اگر هربار چپترین شاخه را دنبال کرده تا به برگ برسیم کوچکترین عنصر این درخت را پیدا میکنیم و از آنجا که ارتفاع درخت را میپیماییم این کار از مرتبه ارتفاع درخت خواهد بود و در این مساله مرتبهی این کار $O(log\ n)$ میباشد.
- محاسبه میانه: برای اینکار مشخص است که باید تمام اعداد درخت رویت شوند و این کار در هیچ صورت مرتبهای کمتر از $O(n)$ نخواهد داشت
- پیدا کردن عنصر x: برای اینکار طبق الگوریتم زیر عمل کرده و کافیست ارتفاع درخت را بپیماییم. ابتدا عنصر x را با ریشه مقایسه کرده و سه حالت پدید میآید:
- اگر x=root پس این عنصر را پیدا کردهایم
- اگر $x<root$ پس در زیر درخت سمت چپ به جستوجو ادامه میدهیم.
- اگر $x>root$ پس در زیر درخت سمت راست به جستوجو ادامه میدهیم.
مشخص است مرتبهی الگوریتم بالا $O(log\ n)$ میباشد چون در نهایت باید ارتفاع درخت را بپیماییم.
- محاسبه مرتبهی x در بین n عدد ذخیره شده: این کار در درخت بدون اطلاعات اضافی در مرتبهی $O(log\ n)$ قابل انجام نخواهد بود زیرا باید هربار تمام زیر درختهای مربوط به x را بپیماییم و تعداد این عناصر را بشماریم اما اگر در سوال ذکر شده بود که درخت ما تعداد عناصر زیر درختهای را نیز در خود ذخیره کرده است با فرض نیاز به جستوجوی x این کار در مرتبه $O(log\ n)$ قابل انجام است.
- مسئله 1- مجموع در زمان$O(1)$ قابل حل است.
- مسئله ۲- مجموع در زمان$O(n)$ قابل حل است.
- مسئله ۳- مجموع در زمان $O(n^2)$ قابل حل است.
گزارهی اول مشخصا نادرست است چون از آنجا که آرایه لزوما مرتب نیست برای پیدا کردن عنصری که برابر با صفر باشد حداقل یک بار باید کل آرایه را جستوجو کنیم و مرتبهی این کار $O(n)$ خواهد بود.
گزارهی دوم نیز نادرست است. برای این کار سه روش زیر وجود دارد:
رویکرد 1: راه ساده برای انجام این کار این است که همهی عناصر را بررسی کنید یعنی هربار عنصر اول را با $n-1$ عنصر بعدی چک کنیم سپس عنصر دوم را با $n-1$ عنصر بعدی چک کنیم و ... عنصر nام را با $n-1$ دیگر چک کنیم این جستجوی دارای مرتبهی $O(n^2)$ است.
رویکرد 2: راه بهتر این است که آرایه را مرتب کنیم. این به $O(nlog\ n)$ نیاز دارد سپس برای هر x در آرایه A با جستوجوی دودویی عنصری که مجموعش با این عنصر برابر با صفر شود پیدا میکنیم که این کار نیز از مرتبهی $O(nlog\ n)$ خواهد بود. حال روش دیگری نیز وجود دارد که برای آرایهای که دارای عناصر اعداد طبیعی است فقط قابل استفاده است و با توجه به اینکه در صورت سوال ذکر شده است اعداد آرایه ما حقیقی هستند نمیتوانیم از آن استفاده کنیم.
رویکرد 3: بهترین راه این است که هر عنصر را در جدول هش (بدون مرتب سازی) درج کنید. این $O(n)$ مرتبه نیاز دارد. سپس برای هر x، ما فقط میتوانیم مکمل آن یعنی عنصری که مجموعش صفر میشود را جستجو کنیم که $O(1)$ است. به طور کلی زمان اجرای این روش $O(n)$ است.
پس با توجه به حقیقی بودن اعضای این آرایه مرتبهی این کار $O(nlog\ n)$ خواهد بود. برای گزارهی سوم از الگوریتم زیر میتوانید استفاده کنید:
آرایه را به ترتیب صعودی مرتب کنید. آرایه را از ابتدا تا انتها پیمایش کنید.
برای هر خانهی i، دو متغیر $l = i + 1$ و $r = n – 1$ ایجاد کنید حال مجموع $[i]A$، $[l]A$ و $[r]َA$ را حساب میکنیم:
- اگر مجموع برابر با صفر باشد، این عناصر را پیدا کردهایم
- اگر مجموع کمتر از صفر باشد، مقدار l را افزایش دهید، چون میخواهیم مقدار جمع بزرگتر شود و آز انجا که آرایه مرتب شده است داریم $A[l+1] > A [l]$ پس با این کار مقدار جمع بزرگتر میشود.
- اگر مجموع بزرگتر از صفر باشد، مقدار r را کاهش دهید، چون میخواهیم مقدار جمع کمتر شود و آز انجا که آرایه مرتب شده است داریم $A[r-1] < A [r]$ پس با این کار مقدار جمع خواهد شد.
مشخص است که مرتبهی الگوریتم بالا برابر با:
$O(nlog\ n)+\ O(n^2)=O(n^2)$
چون برای بخش مرتب سازی $O(nlog\ n)$ داریم و برای بخش دوم الگوریتم برای هر خانهی i این روند را تکرار کرده و بنابراین مرتبه $O(n^2)$ خواهد بود. پس فقط یک عبارت صحیح است.
همانطور که به خاطر دارید متوسط تعداد مقایسه از فرمول زیر بدست میآمد:
متوسط مقایسه $\mathrm{=}\sum^{\mathrm{n}}_{\mathrm{1}}$ تعداد مقایسهها * احتمال
حال برای مسالهی بالا از آنجا که احتمال اینکه این عنصر در بخش دوم باشد 3 برابر بخش اول است به عبارتی اگر احتمال حضور در بخش اول برابر x باشد، احتمال بخش دوم برابر باب 3x خواهد بود و از آنجا که این عنصر حتما در آرایه وجود دارد و احتمال آن برابر با یک هست پس داریم:
$\mathrm{x+3x=1}\mathrm{\to }\mathrm{4x=1}\mathrm{\to }\mathrm{x=}\frac{\mathrm{1}}{\mathrm{4}}$
حال فرض کنید برای آرایهی دیگری مانند B که دارای n خانه میباشد x در این آرایه موجود است. پس احتمال اینکه یک عناصر تصادفی در لیستی که انتخاب میکنیم برابر با x باشد چقدر است؟ خوب اگر احتمال حضور x در همهی خانهها برابر باشد (توزیع یکنواخت) در کل آرایه، این احتمال نیز برابر با $\frac{\mathrm{1}}{\mathrm{n}}$ خواهد بود.
حال باید تعداد دفعات متوسط مقایسه را بدست آوریم برای سادگی اینکار متوسط تعداد را در هر بخش جدا را بدست آوریم و سپس جمع میکنیم (دقت کنید احتمال توزیع یا احتمال وجود در هر خانه برای هر بخش برابر $\frac{\mathrm{1}}{\frac{\mathrm{n}}{\mathrm{2}}}$ خواهد بود).
برای بخش اول تعداد متوسط مقایسه با احتمال حضور $\frac{\mathrm{1}}{\mathrm{4}}$ و احتمال حضور در هر خانهی $\frac{\mathrm{2}}{n}$ برابر است با:
\[\text{ متوسط مقایسه}\mathrm{=}\underbrace{\frac{\mathrm{1}}{\mathrm{4}}}_{\text{احتمال بخش اول}}\mathrm{*}\underbrace{\frac{\mathrm{2}}{\mathrm{n}}}_{\text{احتمال توزیع یکسان}}\mathrm{*}\underbrace{\mathrm{1}}_{\text{با یک مقایسه به جواب برسیم}}\mathrm{+}\underbrace{\frac{\mathrm{1}}{\mathrm{4}}}_{\text{احتمال بخش اول}}\mathrm{*}\underbrace{\frac{\mathrm{2}}{\mathrm{n}}}_{\text{احتمال توضیع یکسان}}\mathrm{*}\underbrace{\mathrm{2}}_{\text{با دو مقایسه به جواب برسیم}}\mathrm{+}\underbrace{\frac{\mathrm{1}}{\mathrm{4}}}_{\text{احتمال بخش اول}}\mathrm{*}\underbrace{\frac{\mathrm{2}}{\mathrm{n}}}_{\text{احتمال توزیع یکسان}}\mathrm{*}\underbrace{\mathrm{3}}_{\text{با دو مقایسه به جواب برسیم}}\mathrm{+}\mathrm{\cdots }\mathrm{+}\underbrace{\frac{\mathrm{1}}{\mathrm{4}}}_{\text{احتمال بخش اول}}\mathrm{*}\underbrace{\frac{\mathrm{2}}{\mathrm{n}}}_{\text{احتمال توزیع یکسان}}\mathrm{*}\underbrace{\frac{\mathrm{n}}{\mathrm{2}}}_{\text{با}\frac{\mathrm{n}}{\mathrm{2}}\text{مقایسه به جواب برسیم}}\mathrm{=}\frac{\mathrm{1}}{\mathrm{4}}\mathrm{*}\frac{\mathrm{2}}{\mathrm{n}}\mathrm{*}\mathrm{(1+2+3+}\mathrm{\cdots }\mathrm{+}\frac{\mathrm{n}}{\mathrm{2}}\mathrm{)=}\frac{\mathrm{1}}{\mathrm{4}}\mathrm{*}\frac{\mathrm{2}}{\mathrm{n}}\mathrm{*}\frac{\frac{\mathrm{n}}{\mathrm{2}}\left(\frac{\mathrm{n}}{\mathrm{2}}\mathrm{+1}\right)}{\mathrm{2}}=\frac{n}{16}+\frac{1}{8}\]
برای بخش دوم تعداد متوسط مقایسه با احتمال حضور $\frac{3}{4}$ و احتمال حضور در هر خانهی $\frac{2}{n}$ برابر است با:
\[\text{ متوسط مقایسه}\mathrm{=}\underbrace{\frac{\mathrm{3}}{\mathrm{4}}}_{\text{احتمال بخش اول}}\mathrm{*}\underbrace{\frac{\mathrm{2}}{\mathrm{n}}}_{\text{احتمال توزیع یکسان}}\mathrm{*}\underbrace{(\frac{\mathrm{n}}{\mathrm{2}}+1)}_{\text{با}(\frac{\mathrm{n}}{\mathrm{2}}+1)\text{مقایسه به جواب برسیم}}\mathrm{+}\underbrace{\frac{\mathrm{3}}{\mathrm{4}}}_{\text{احتمال بخش اول}}\mathrm{*}\underbrace{\frac{\mathrm{2}}{\mathrm{n}}}_{\text{احتمال توزیع یکسان}}\mathrm{*}\underbrace{(\frac{\mathrm{n}}{\mathrm{2}}+2)}_{\text{با}\frac{\mathrm{n}}{\mathrm{2}}+2\text{مقایسه به جواب برسیم}}\mathrm{+}\underbrace{\frac{\mathrm{3}}{\mathrm{4}}}_{\text{احتمال بخش اول}}\mathrm{*}\underbrace{\frac{\mathrm{2}}{\mathrm{n}}}_{\text{احتمال توزیع یکسان}}\mathrm{*}\underbrace{(\frac{\mathrm{n}}{\mathrm{2}}+3)}_{\text{با}(\frac{\mathrm{n}}{\mathrm{2}}+3)\text{مقایسه به جواب برسیم}}\mathrm{+}\mathrm{\cdots }\mathrm{+}\underbrace{\frac{\mathrm{1}}{\mathrm{4}}}_{\text{احتمال بخش اول}}\mathrm{*}\underbrace{\frac{\mathrm{2}}{\mathrm{n}}}_{\text{احتمال توزیع یکسان}}\mathrm{*}\underbrace{\mathrm{n}}_{\text{با}\frac{\mathrm{n}}{\mathrm{2}}\text{مقایسه به جواب برسیم}}\mathrm{=}\frac{\mathrm{3}}{\mathrm{4}}\mathrm{*}\frac{\mathrm{2}}{\mathrm{n}}\mathrm{*}\mathrm{(}(\frac{\mathrm{n}}{\mathrm{2}}+1)\mathrm{+}(\frac{\mathrm{n}}{\mathrm{2}}+2)\mathrm{+}(\frac{\mathrm{n}}{\mathrm{2}}+3)\mathrm{+}\mathrm{\cdots }\mathrm{+}\mathrm{n)=}\frac{\mathrm{3}}{\mathrm{4}}\mathrm{*}\frac{\mathrm{2}}{\mathrm{n}}\mathrm{*}\frac{\frac{\mathrm{n}}{\mathrm{2}}\left(\mathrm{n+}(\frac{\mathrm{n}}{\mathrm{2}}+1)\right)}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{*}\frac{\mathrm{2}}{\mathrm{n}}\mathrm{*}\frac{\frac{\mathrm{n}}{\mathrm{2}}\left(\frac{\mathrm{3n}}{\mathrm{2}}+1\right)}{\mathrm{2}}=\frac{9n}{16}+\frac{3}{8}\]
پس تعداد متوسط مقایسه برای کل آرایه برابر است با:
تعداد متوسط مقایسه نیمه دوم + تعدادمتوسط مقایسه نیمه اول که نزدیکترین پاسخ گزینه 2 میباشد $=(\frac{n}{16}+\frac{1}{8})+(\frac{9n}{16}+\frac{3}{8})=\frac{10n}{16}+\frac{4}{8}=\frac{5n}{8}+\frac{1}{2}$
یاددآوری: جستجوی خطی در آرایه نامرتب استفاده میشود. اگر به دنبال $n$ هستیم، $n$ را با عنصر اول آرایه مقایسه میکنیم، اگر برابر بود که تمام (میگوییم یافتیم) اما اگر برابر نبود میرویم سراغ عنصر دوم و...
حداقل مقایسه = $1$
یا آخری است یا اصلا در آرایه نیست $= n \to $ حداکثر مقایسه $n$
فرض کردیم $n$ حتما درون آرایه است $= \frac{n+1}{2}\rightarrow\theta\left(n\right)\rightarrow$ متوسط مقایسه
فرض کنیم $n$ درون آرایه است:
متوسط مقایسه = $\sum^n_1{\text{تعداد مقایسه}}\times \text{احتمال}$
احتمال وجود $n$ در هر خانه = $\frac{1}{n}$
متوسط تعداد مقایسه = $\frac{1}{n}\times 1+\frac{1}{n}\times 2+\frac{1}{n}\times 3+\dots +\frac{1}{n}\times n=\frac{1}{n}\left(1+2+3+\dots +n\right)$
$=\frac{n\left(n+1\right)}{n\times2}=\frac{n+1}{2}$
با احتمال $n$ درون آرایه است
احتمال وجود $n$ در هر خانه = $\frac{P}{n}$
احتمال عدم وجود $n$ در آرایه = $1-P$
متوسط مقایسه = $\frac{P}{n}\times1+\frac{P}{n}\times2+\ldots+\frac{P}{n}\times n+\left(1-P\right)\times n=\frac{P}{n}\times\frac{n\left(n+1\right)}{2}+\left(1-P\right)n$
تست) فرض کنید $X$ به احتمال 50 درصد داخل آرایه است، برای یافتن $n$ با جستجوی خطی بطور متوسط چندتا عنصر آرایه را باید چک کنیم؟
- $\frac{\mathrm{1}}{\mathrm{2}}$
- $\frac{\mathrm{3}}{\mathrm{4}}$
- $\frac{\mathrm{2}}{\mathrm{3}}$
- $\frac{\mathrm{1}}{\mathrm{3}}$
$\frac{1}{2}\times\frac{n+1}{2}+\frac{1}{2}n=\frac{3}{4}n+\frac{1}{2}$
رابطه بازگشتی الگوریتم بالا به صورت زیر خواهد بود:
$T(n)=3T(\frac{n}{3})+n$
مشخص است که مرتبهی این رابطه بازگشتی $O(nlog\ n)$ خواهد بود حال باید صحیح بودن این الگوریتم چک شود برای این کار کافیست مثالی بزنیم مثلا آرایه زیر را در نظر بگیرید:
مشکل الگوریتم ذکر شده در این بخش است که در سوال عنوان شده در هر زیر آرایه فقط یک عضو پر تکرار را مییابیم پس یعنی اگر در زیر آرایهای دو عضو پر تکرار باشد ممکن است یکی را از دست بدهیم.
مشکل الگوریتم ذکر شده در این بخش است که در سوال عنوان شده در هر زیرآرایه فقط یک عضو پرتکرار را مییابیم پس یعنی اگر در زیرآرایهای دو عضو پرتکرار باشد ممکن است یکی را از دست بدهیم مثلاً داریم:
البته مشکل دیگری نیز این الگوریتم دارد، که آن مشکل این است که ممکن است عضوی مانند x در کل عضو با بیشترین تکرار باشد ولی در هیچیک از سه قسمت آرایه عضو با بالاترین تکرار نباشد، به مثال زیر دقت کنید:
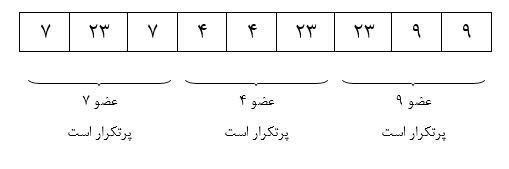
حال بررسی میکنیم که هریک از اعداد 7 و 4 و 9 چندبار در کل آرایه تکرار شده است (مرتبه اینکار $\theta \left(n\right)$ است)
بنابراین الگوریتم مطرح شده دارای مرتبهی $O(nlog\ n)$ خواهد بود اما لزوما به درستی کار نخواهد کرد.
کافیست از ایدهی جستوجوی دودویی کمک بگیریم و به این صورت عمل میکنیم.
ابتدا عنصر i آرایه A یعنی $ A[i]$ را بررسی میکنیم حال سه حالت پدید میآید:
- اگر $A[i]>x$ بود یعنی عناصر با مقادیر کوچکتر باید دنبال x بگردیم پس مانند جستوجوی دودویی عمل میکنیم یعنی $\frac{i}{2}=mid$ در نظر گرفته و به صورت زیر عمل میکنیم:
- اگر $A[mid]=x$ عنصر را در آرایه یافتیم.
- اگر $A[mid]<x$ پس در بازهی $A[mid+1\cdots i]$ جستوجو ادامه میدهیم.
- اگر $A[mid]>x$ پس در بازهی $A[1\cdots mid-1]$ جستوجو ادامه میدهیم.
- اگر $A[i]<x$ بود یعنی عنصر x ممکن است در آرایه باشد، پس اندیس را دوبرابر کرده یعنی $A[i*2]$ و به جستوجو ادامه میدهیم.
- اگر $A[i]=x$ بود یعنی عنصر x را پیدا کردهایم.
برای شروع مقدار $i=1$ در نظر گرفته و جستوجو را در آرایه اغاز میکنیم. مشخص است که مرتبهی الگوریتم بالا $O\left(\log{n}\right)$ است.
به ازای دو رأس u و v داده شده و پارامتر ورودی k ، آیا تعداد کوتاه ترین مسیرها بين u و v حداقل k است؟ کدام گزینه در مورد این مسئله درست است؟
دقت کنید برای پیدا کردن
حال با توجه به اینکه وزن همهی یالها برابر است با استفاده از BFS میتوانیم با مرتبهی بهتری این کار را انجام دهیم:
در پیمایش BFS یک آرایه به نام $Distance$ تعریف میکنیم، سپس Distance راس شروع را صفر میدهیم هر راسی که راس شروع ملاقات کرد $Distance$ را برابر با 1 میدهیم سپس اگر راس x، راس y را ملاقات کند $d[y]=d[x]+1$ در انتها فاصله هر راس به راس شروع مشخص است در واقع $distance$ عمق هر نود نسبت به نقطه شروع را میدهد.
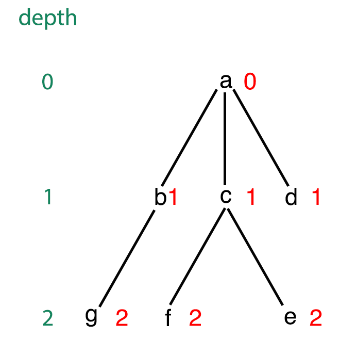
حال اگر BFS با ماتریس مجاورتی پیاده شود دارای مرتبه $\theta(n^2)$ و اگر با لیست مجاورتی پیاده شود دارای مرتبه $\theta(n+e)$ است. در نتیجه بهترین مرتبه برای این کار $\theta(n+e)$ است.
دقت کنید در این سوال از ما تعداد کوتاهترین مسیر بین دو راس خواسته شده است بنابراین کافیست در الگوریتم بالا فقط اگر در طی BFS در طول مسیری به راس مقصد برخوردیم هربار با استفاده از شمارندهای این تعداد برخوردها بشماریم و در نهایت تعداد مسیرهای یافت شده را با k مقایسه کنیم و پس همچنان در مرتبه \theta(n+e) میتوان به پاسخ رسید.
یاددآوری:
الگوریتم برای پیدا کردن کوتاهترین مسیر از راس مشخص به همهی راسها:
- الگوریتم بلمن فورد: برای گرافهایی که یال منفی نیز دارند جواب میدهد و اگر سیکل منفی قابل دسترس از راس مورد نظر وجود داشته باشد آن سیکل را تشخیص داده و اعلام میکند. این الگوریتم به این صورت کار میکند ابتدا همه رئوس را مقداردهی اولیه میکند (فراخوانی init) سپس $n-1$ بار که n تعداد رئوس گراف است، هربار روی همهی یالها به ترتیب دلخواهی که خودش از اول مشخص کرده عمل relax کردن را انجام میدهد. (مرتبه بلمن فورد با لیست مجاورتی برابر $\theta(ne)$ و با ماتریس برابر با $\theta\left(n^3\right)$ است.)
- الگوریم دایجسترا: این الگوریتم فرض میکند که گراف یال با وزن منفی ندارد و به جای اینکه $n-1$ بار همهی یالها relax کند، فقط یک بار اینکار را انجام میدهد ولی دیگر نمیتواند به هر ترتیب دلخواهی باشد. بنابراین برای وزن منفی ممکن است نادرست پاسخ بدهد.
نکته)مرتبه دایجسترا
- در صورت استفاده از ماتریس مجاورتی: $\theta(\mathbf{n}^\mathbf{2})$
- در صورت استفاده از لیست مجاورتی:
\[\left\{\ \ \ \begin{array}{c}binary\ minheap\mathrm{\Rightarrow }\mathrm{T(n)}\mathrm{\in }\mathrm{\ }\theta \mathrm{(e\ log\ n)} \\ fibonacci\ heap\mathrm{\ }\mathrm{\Rightarrow }\mathrm{T(n)}\mathrm{\in }\mathrm{\ }\theta \mathrm{(e+\ n\ log\ n)} \end{array}\right.\]
الگوریتم پیدا کردن کوتاهترین فاصله بین هر دو راس:
الگوریتم فلوید: یک الگوریتم با استفاده از برنامه نویسی پویا برای گرافهای بی جهت و جهتدار با یالهای منفی و مثبت اما بدون سیکل منفی است و مانند الگوریتم بلمن فورد اگر سیکل منفی وجود داشته باشد ان را تشخیص میدهد واعلام میکند. الگوریتم فلوید در $\theta(\mathbf{n}^\mathbf{3})$ همهی مسیرهای ممکن در یک گراف بین هر جفت راس را مقایسه میکند.
شبیه سازی الگوریتم فلوید را در لینک زیر میتوانید مشاهده کنید:
پاسخ تشریحی هوش مصنوعی کنکور ارشد کامپیوتر 1401
۷۳- فرض کنید در یک مسئله جستجو که توسط الگوریتم $A^*$ با جستجوی درختی حل میشود، دو تابع مکاشفه متفاوت قابل قبول$h_1$ و $h_2$ قابل تصور باشند. اگر از $h_1$ و $h_2$ با استفاده شود، به ترتیب $n_1$ و $n_2$ گره قبل از توقف الگوریتم توسعه داده میشوند. در این خصوص، کدام مورد درست است؟
در صورت سوال اشاره شده است که هر دو تابع مکاشفهای قابل قبول هستند به این معنی که در تمامی گرهها
$h_1(s), h_2(s) \le h^*(s)$ برقرار میباشد و از آنجایی که شرط قابل قبول بودن برای هر دو هیوریستیک برقرار است، با استفاده از هر دو تابع مسیر بهینه حاصل میشود و در واقع فرق هر کدام از این هیوریستیکها در تعداد گرههایی است که بسط میدهند.
گزینه ۱ و ۲ : اگر تعداد گرههای توسعه داده شده با استفاده از یک هیوریستیک کمتر مساوی دیگری باشد نمیتوان لزوما نتیجه گرفت که به ازای تمام گرهها یکی از یکی دیگر بزرگتر است چرا که ممکن است حالتی وجود داشته باشد که در برخی گرهها هیوریستیک اول بزرگتر باشد و در برخی دیگر هیوریستیک دوم اما باز هم در مجموع یکی تعداد گره بیشتری را بسط دهد.
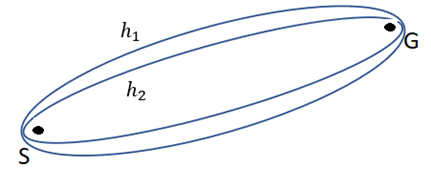
گزینه ۳ و ۴ : در گزینه سوم و چهارم به این اشاره شده است که $h_1(s) \le h_2(s)$ میباشد یعنی مقادیر هیوریستیک دوم برای هر گره به هزینه واقعی آن گره تا هدف یعنی h* نزدیکتر است (به عبارتی میتوان گفت این هیوریستیک از دیگری دقیق تر است) در این حالت میتوان نتیجه گرفت فضای حالتی را که هیوریستیک دوم نیاز دارد بررسی کند تا مسیر بهینه را پیدا کند کوچکتر مساوی هیوریستیک اول است و در نتیجه تعداد گره کمتری را برای رسیدن به هدف بسط میدهد. شکل زیر بیانگر فضای جستجو برای دو هیوریستیک است اگر بدانیم که $h_1(s) \le h_2(s)$ : (البته در حالت تساوی خطوط روی هم میافتند)
- در نهایت، همه K جواب نهایی، به بهینههای محلی متفاوت همگرا میشوند.
- این جستجو معادل با K جستجوی تپهنوردی مستقل از هم است.
- با افزایش K، احتمال همگرایی به یک حالت بهینه عمومی کاهش مییابد.
جستجو پرتو محلی :
این روش مشابه روش تپهنوردی است با این تفاوت که در این الگوریتم در هر مرحله بهجای اینکه فقط بهترین گره را در حافظه نگهداریم، k بهترین گره را در هر مرحله ذخیره میکنیم. روش کار این الگوریتم به این صورت است که در ابتدا با k گره تصادفی شروع میکنیم و سپس در هر مرحله از بین تمام همسایههای این k گره، k بهترین گره را برای مرحله بعدی انتخاب میکنیم به عبارتی در این حالت اگر یکی از گرههای همسایه تولید شده هدف باشد که الگوریتم به جواب رسیده است در غیر اینصورت به سراغ k بهترین همسایه میرویم و این کار را تا رسیدن به هدف تکرار میکنیم.
عبارت اول : لزوما درست نیست و ممکن است تعدادی از k جواب نهایی به بهینههای محلی یکسانی همگرا شوند (فرض کنید که مثلا یک قله داریم و هر کدام از جوابها از یک طرف قله به آن همگرا میشوند)
عبارت دوم : این عبارت نیز درست نیست واین دو الگوریتم با هم مشابه هستند اما معادل نیستد چرا که در روش اجرای k جستجو تپهنوردی مستقل هیچگونه اطلاعاتی بین گرهها به اشتراک گذاشته نمیشود و هر کدام به صورت مستقل اجرا میشوند در حالیکه در روش پرتو محلی انتخاب k بهترین همسایه از بین همسایههای تمامی k گره جاری انتخاب میشود و مثلا ممکن است چند همسایه از یک گره انتخاب شود و از گرههایی هیچ همسایهای انتخاب نشود که همانطور که اشاره شده با اجرای موازی k جستجو تپهنوردی متفاوت است.
عبارت سوم : در روش جستجو پرتو محلی هر چه k دارای تنوع کمتری باشد در نتیجه ناحیه کوچکتری از مسئله جستجو میشود و این روش کارایی خود را در این حالت از دست میدهد. حال هر چه k عددی بزرگتری باشد در صورتی که جمعیت اولیه به صورت تصادفی انتخاب شود و این عدد k بزرگتر منجر به تنوع بیشتر شود میتوان گفت در این حالت احتمال همگرایی به یک حالت بهینه عمومی افزایش مییابد چرا که احتمال دستیابی به بهینه محلی و ناحیهای که مورد بررسی قرار میگیرد در این حالت بیشتر میشود.
در نتیجه هیچکدام از گزارههای بیان شده در این سوال درست نیستند.
نکات :
- اگر احتمال موفقیت الگوریتم جستجو محلی با شروع مجدد تصادفی در هر بار برابر p باشد آنگاه متوسط تعداد دفعات شروع مجدد برای رسیدن به پاسخ بهینه عمومی در این الگوریتم برابر $\frac{1}{p}$ میباشد.
(برای اثبات نکته بالا باید از تعریف امید ریاضی برای متغیر دارای توزیع هندسی کمک گرفت :
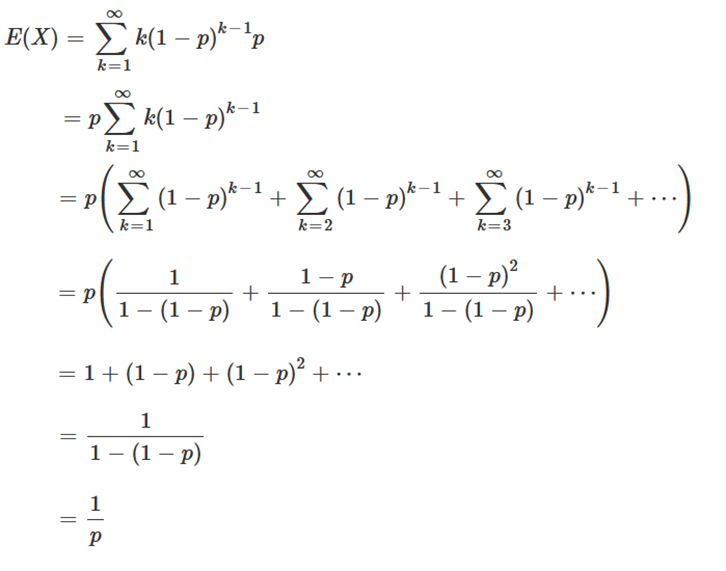
- اگر احتمال موفقیت الگوریتم جستجو محلی با شروع مجدد تصادفی در هر بار برابر p باشد آنگاه تعداد گامهای مورد انتظار برای رسیدن به پاسخ بهینه برابر است با:
تعداد کل گامها : ( تعداد گامها در تپهنوردی در حالت موفق) + (تعداد گامها در تپهنوردی در حالت ناموفق) $(\frac{1}{p}-1)$
در صورت سوال احتمال رسیدن به بهینه عمومی با حداکثر دوبار جستجو خواسته شده است که این احتمال را میتوان به صورت احتمال رسیدن به بهینه محلی در اولین جستجو و احتمال نرسیدن در اولین جستجو و رسیدن در دومین جستجو در نظر گرفت. طبق روابط زیر میتوان این احتمال را محاسبه کرد.
از آنجایی که متوسط تعداد دفعات شروع مجدد برای رسیدن به پاسخ بهینه عمومی در این الگوریتم ۵۰ داده شده است پس طبق نکته اول احتمال موفقیت الگوریتم جستجو محلی با شروع مجدد تصادفی در هر بار برابر میباشد.
احتمال رسیدن به بهینه محلی در اولین جستجو : $\frac{1}{50}=0/02$
احتمال رسیدن به بهینه محلی در اولین جستجو : $\frac{49}{50} × \frac{1}{50}=0/0196$
که مجموع دو احتمال بالا برابر است با 0/0196 که معادل گزینه سوم است.
در صورت سوال اشاره شده است که احتمال درستی یا نادرستی گزارههای P, Q, R, S یکسان است به این معنی که برای مثال $P(S)\ =\ P(\neg S)\ =\ 0.5$ برقرار است. همچنین میدانیم که گزاره شرطی $P\ \to \ \sim Q$ نادرست است و این گزاره فقط در حالتی میتواند نادرست باشد که P = True و Q = True باشد. از طرفی صورت سوال از ما احتمال درستی گزاره شرطی مرکب $\ (\sim Q\ \to \ R)\ \wedge \ (P\ \to \ S)$ را خواسته است که برای به دست آوردن این احتمال باید حالتی که این گزاره در آنها درست است و احتمال آن حالات را بدست آوریم. در ابتدا مقادیر معادل P و Q را جایگذاری میکنیم.
$(\sim Q\ \to \ R)\ \wedge \ (P\ \to \ S) \\ \left(\sim True\to R\right)\wedge \left(True\to S\right) \\ \left(False\to R\right)\wedge \left(True\to S\right)$
در مرحله بعد برای این که گزاره بالا برقرار باشد باید هر یک از گزارههای $True \rightarrow S$ و $(False \rightarrow R)$ برقرار باشند. بخش $(False \rightarrow R)$ که مستقل از اینکه R چه مقداری دارد همیشه برقرار است اما بخش $True \rightarrow S$ فقط در صورتی که S = True باشد برقراراست با این شرایط احتمال درستی گزاره شرطی مرکب $(\sim Q\ \to \ R)\ \wedge \ (P\ \to \ S)$ برابر است با :
$P((\sim Q\ \to \ R)\ \wedge \ (P\ \to \ S)\ =\ True\ \ |(\ P\ \to \ \sim Q)\ =\ False)$
$\ =\ \frac{P(((\sim Q\ \to \ R)\ \wedge \ (P\ \to \ S)\ =\ True)\ \ \wedge \ ((P\ \to \ \sim Q\ )\ =\ False)\ )\ }{P((P\ \to \ \sim Q\ )\ =\ False)\ )}$
$=\frac{P\left(\mathrm{P=T,Q=T,R=T,S=T}\right)+P\left(\mathrm{P=T,Q=T,R=F,S=T}\right)}{P\left(\mathrm{P=T,Q=T}\right)}\ =\ \frac{0.5\times \ 0.5\ \times 0.5\ \times 0.5\ +\ 0.5\times \ 0.5\ \times 0.5\ \times 0.5}{4\left(0.5\times 0.5\times 0.5\times 0.5\right)}\ =\ 0.5$
\[\mathbf {A \rightarrow B \rightarrow C \rightarrow D}\]
| $\mathbf{P(D =}\text{0}\text{ | C=}\text{0}\text{)=}\text{0/1}$ | $P(C = \text{0}\text{ | B=}\text{0}\text{)=}\text{0/1}$ | $P(A = \text{0}\text{)=}\text{0/5}$ |
| $\mathbf{P(D =}\text{0}\text{ | C=}\text{0}\text{)=}\text{0/8}$ | $P(C = \text{0}\text{ | B=}\text{0}\text{)=}\text{0/8}$ | $P(B = \text{0}\text{ | A=}\text{0}\text{)=}\text{0/8}$ |
| $P(B = \text{0}\text{ | A=}\text{0}\text{)=}\text{0/1}$ |
در این سوال صرف نظر از ایکه نمونهبرداری Gibbs چیست و چگونه عمل نمونهبرداری را انجام میدهد میتوان به صورت زیر به حل سوال پرداخت.
توزیع احتمال توأم متغیرها براساس مدل شبکه بیزی داده شده در صورت سوال را میتوان به صورت زیر نوشت :
$P\left(A,B,C,D\right)=P\left(A\right)P\left(B\mathrel{\left|{ A}\right.}\right)P\left(C\mathrel{\left|\right.}B\right)P\left(D\mathrel{\left|\right.}C\right)$
در صورت سوال گفته شده است که تا به اینجای کار متغیرهای A=0, B=1, D=0 نمونهبرداری شده اند و سپس احتمال شرطی زیر خواسته شده است:
$P\left(C=0\mathrel{\left|{C=0 \mathrm{A=0,B=1,D=0}}\right.}\mathrm{A=0,B=1,D=0}\right)\ =\ $
$\mathrm{\ }\frac{P\left(C=0,\mathrm{A=0,B=1,D=0}\right)}{P\left(C=1,\mathrm{A=0,B=1,D=0}\right)\mathrm{+}P\left(C=0,\mathrm{A=0,B=1,D=0}\right)}$
$=\ \frac{P(A=0)P(B=1|A=0)P(C=0|B=1)P(D=0|C=0) }{P(A=0)P(B=1|A=0)P(C=1|B=1)P(D=0|C=1)+P(A=0)P(B=1|A=0)P(C=0|B=1)P(D=0|C=0)}$
$=\ \frac{0.5\times \ 0.2\ \times \ 0.1\times 0.8\ }{0.5\times \ 0.2\ \times \ 0.1\times 0.8\ +\ 0.5\times \ 0.2\ \times \ 0.9\times 0.1}\ =\ \frac{0.8\ }{0.8\ +\ \ 0.9}\ =\ \frac{8}{17}$

ابتدا به دستهبند naïve bayes و نحوه عملکرد آن را معرفی میکنیم و سپس به پاسخ سوال میپردازیم.
الگوریتم دسته بندی بیز ساده naïve bayes
الگوریتم دسته بندی بیز ساده naïve bayes از دو کلمه naïve و bayes تشکیل شده است. به این دستهبند Naive میگویند زیرا فرض بر آن است که وقوع یک ویژگی خاص مستقل از وقوع سایر ویژگیها باشد و به آن Bayes گفته میشود زیرا به اصل قضیه بیز بستگی دارد.
قضیه بیز را میتوان یک مدل برمبنای احتمال شرطی در نظر گرفت. فرض کنید $X=(x_1,x_2,..., x_n)$ برداری از n ویژگی را بیان کند که به صورت متغیرهای مستقل هستند. به این ترتیب میتوان احتمال رخداد $C_k$ یعنی $p(C_k|x_1,x_2,...,x_n)$ را به عنوان یکی از حالتهای کلاس رخدادهای مختلف به ازاء kهای متفاوت، به شکل زیر نمایش داد.
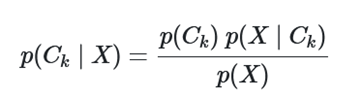
به این ترتیب برای محاسبه احتمال $p(C_k|x_1,x_2,...,x_n)$ کافی است از «احتمال توام» (Joint Probability) کمک بگیریم و به کمک احتمال شرطی با توجه به استقلال متغیرها، آن را ساده کنیم.
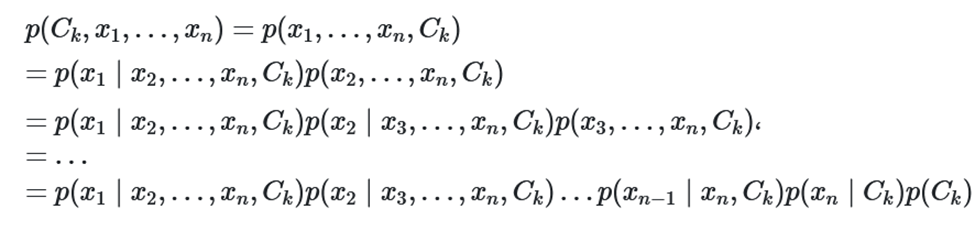
با فرض استقلال مولفهها یا ویژگیهای xiها از یکدیگر میتوان احتمالات را به شکل سادهتری نوشت. کافی است رابطه زیر را در نظر بگیریم.
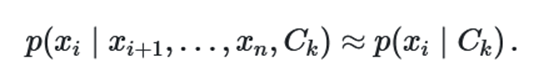
به این ترتیب احتمال توام را به صورت حاصلضرب احتمال شرطی میتوان نوشت.
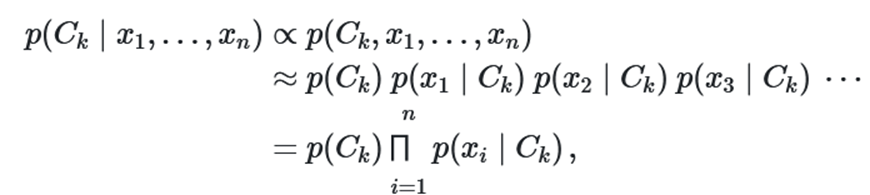
نکته: در رابطه بیز، مخرج کسر در همه محاسبات یکسان و ثابت است در نتیجه میتوان احتمال شرطی را متناسب با احتمال توام در نظر گرفت.
در مرحله بعد برای ساختن یک دستهبند از روش حداکثر درستنمایی استفاده میکنیم و بر اساس رابطه بدست آمده در بالا احتمال تعلق به هر کلاس را به صورت زیر محاسبه کرده و محتملترین کلاس را برای داده انتخاب میکنیم.
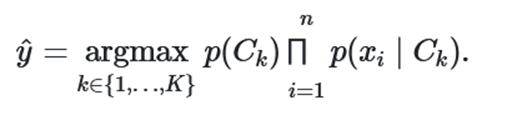
دستهبندی متن به کمک دستهبندی بیز ساده
در این بخش به کمک تکنیک دستهبند بیز، مسئله تفکیک متنها را حل میکنیم. قرار است براساس محتویات اسناد متنی آنها را در دستههای مشخصی جای دهیم. برای مثال نامههای موجود در صندوق پست الکترونیکی را به دو گروه اصلی (کلاس یک) و هرزنامه (کلاس دو) طبقهبندی کنیم. فرض کنید که احتمال اینکه کلمه $w_i$ از یک سند در دسته C قرار گیرد برابر با $p(w_i|C)$ باشد. به این ترتیب مشخص است که این احتمال به طول سند و خصوصیات دیگر سند مرتبط نیست در نتیجه کلمات به طور تصادفی در متن توزیع شدهاند. پس شرط استقلال وجود دارد. در مرحله بعد برای محاسبه احتمال تعلق نامه به هر کدام از کلاسها از رابطه بدست آمده در بخش قبل استفاده کرده و کلاسی را که این احتمال برای آن بیشتر بدست آمده است را بعنوان کلاس متن در نظر میگیریم.
پاسخ سوال :
در صورت سوال به این اشاره شده است که در زمان ارزیابی با متنی رو به رو شدیم که واژگانی دارد که همه واژگان آن در دادههای آموزشی کلاس دوم دیده شدهاند این به این معنی است که احتمال $p(w_i|c_2)$ مقداری مثبت است که براساس میزان تکرار واژه $w_i$ میتواند بزرگ یا کوچک باشد. همچنین صورت سوال گفته است که متن مورد ارزیابی واژگانی دارد که در دادههای آموزش کلاس اول دیده نشده است و این به این معنی است که $p(w_i|c_1)$ در واقع برای آن صفر است البته این مقدار را در عمل برابر با صفر در نظر نمیگیرند چرا که مقدار صفر در ضرب با مقدار احتمال سایر کلمات احتمال بقیه کلمات را نیز نادیده میگیرد و در نهایت مقدار احتمال کل برابر صفر بدست میآید در نتیجه برای کلماتی که آن را در داده آموزش این کلاس نداشتیم مقدار آن را یک مقدار بسیار کوچک در نظر میگیرند. از طرفی از آن جایی که دو کلاس داریم با فرض اینکه احتمال پیشین هر کدام از کلاسها برابرست در هنگام محاسبه عبارت زیر با مفروضات صورت سوال، مقدار احتمال برای کلاس دوم بیشتر از کلاس اول بدست میآید و میتوان گفته دستهبند متن دیده شده را الزاما به کلاس دوم دستهبندی خواهد کرد.
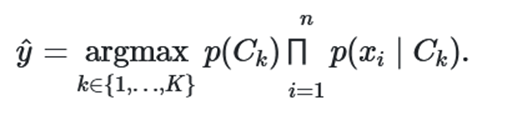
| $\mathbf{A\ \ \ \rightarrow \ \ \ \ B}$ | ||
| $\downarrow \ \ \ \ \ \ \ \ \ \ \ \ \ \ \downarrow$ | ||
| $C\ \ \ \ \rightarrow \ \ \ D$ | ||
| $\mathbf{P(D =}\text{0}\text{ | B=}\text{1}\text{ ,C=}\text{0}\text{)=}\text{0/5}$ | $P(B = \text{0}\text{ |A=}\text{0}\text{)=}\text{0/8}$ | $P(A = \text{0}\text{)=}\text{0/5}$ |
| $\mathbf{P(D =}\text{0}\text{ | B=}\text{0}\text{ , C=}\text{1}\text{)=}\text{0/5}$ | $P(B = \text{0}\text{ | A=}\text{1}\text{)=}\text{0/2}$ | $P(C = \text{0}\text{ | A=}\text{0}\text{)=}\text{0/1}$ |
| $\mathbf{P(D =}\text{0}\text{ | B=}\text{1}\text{ , C=}\text{1}\text{)=}\text{0}$ | $P(D = \text{0}\text{ | B=}\text{0}\text{ , C=}\text{0}\text{)=}\text{1}$ | $P(C = \text{0}\text{ | A=}\text{1}\text{)=}\text{0/8}$ |
توزیع احتمال توأم متغیرها براساس مدل شبکه بیزی داده شده در صورت سوال را میتوان به صورت زیر نوشت :
$P(A, B,C,D)=P(A)P(B|A)P(C|A)P(D|C,B)$
از طرفی صورت سوال مقدار $P(A=1| B=0, D=1)$ را خواسته است که برای محاسبه آن داریم :
$P(A=1|B=0,D=1)=\frac{P(A=1,B=0,D=1)}{P(B=0,D=1)}$
$=\ \frac{\mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1,\ }C=1\right)+\ \mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1,\ C=0}\right)}{\mathrm{P}\left(\mathrm{A=1,C=1},\mathrm{\ B=0,\ D=1}\right)+\ \mathrm{P}\left(\mathrm{A=1},C=0,\mathrm{\ B=0,\ D=1}\right)\mathrm{+\ P}\left(\mathrm{A=0},C=0,\ \mathrm{\ B=0,\ D=1}\right)+\ \mathrm{P}\left(\mathrm{A=0},\ C=1,\mathrm{\ B=0,\ D=1}\right)}$
برای محاسبه عبارت صورت کسر بالا داریم :
$\mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1,\ }C=1\right)+\ \mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1,\ C=0}\right)=\ $
$P\left(A=1\right)P\left(B=0\mathrel{\left|{B=0 A=1}\right.}A=1\right)P\left(C=1\mathrel{\left|{C=1 A=1}\right.}A=1\right)P\left(D=1\mathrel{\left|{D=1 C=1,\ B=0}\right.}C=1,\ B=0\right)+\ P\left(A=1\right)P\left(B=0\mathrel{\left|{B=0 A=1}\right.}A=1\right)P\left(C=0\mathrel{\left|{C=0 A=1}\right.}A=1\right)P\left(D=1\mathrel{\left|{D=1 C=0,\ B=0}\right.}C=0,\ B=0\right)=\ $
$P(A=1)P(B=0| {B=0 A=1}A=1)\ (\ P(C=1| {C=1 A=1}A=1)P(D=1| {D=1 C=1,\ B=0 }C=1,\ B=0)+\ P(C=0| {C=0 A=1 }A=1)P(D=1| {D=1 C=0,\ B=0 }C=0,\ B=0))$
$=0.5\ \times 0.2\ \ \left(\ 0.2\times 0.5\ +\ \ 0.8\times 0\right)=0.01$
و همچنین مخرج کسر نیز بهصورت زیر محاسبه میشود :
$\mathrm{P}\left(\mathrm{A=1,C=1},\mathrm{\ B=0,\ D=1}\right)+\mathrm{P}\left(\mathrm{A=1},C=0,\mathrm{\ B=0,\ D=1}\right)\mathrm{+P}\left(\mathrm{A=0},C=0,\ \mathrm{B=0,\ D=1}\right)+\mathrm{P}\left(\mathrm{A=0},\ C=1,\mathrm{\ B=0,\ D=1}\right) = $
$0.01+\ P\left(A=0\right)P\left(B=0\mathrel{\left| {B=0 A=0}\right. }A=0\right)P\left(C=0\mathrel{\left| {C=0 A=0}\right. }A=0\right)P\left(D=1\mathrel{\left|\vphantom{D=1 C=0,\ B=0}\right. }C=0,\ B=0\right)+\ P\left(A=0\right)P\left(B=0\mathrel{\left| {B=0 A=0}\right. }A=0\right)P\left(C=1\mathrel{\left| {C=1 A=0}\right. }A=0\right)P\left(D=1\mathrel{\left| {D=1 C=1,\ B=0}\right. }C=1,\ B=0\right)=$
$=0.01+\ \ P\left(A=0\right)P\left(B=0\mathrel{\left| {B=0 A=0}\right. }A=0\right)\ \left(P\left(C=0\mathrel{\left| {C=0 A=0}\right. }A=0\right)P\left(D=1\mathrel{\left| {D=1 C=0,\ B=0}\right. }C=0,\ B=0\right)+P\left(C=1\mathrel{\left| {C=1 A=0}\right. }A=0\right)P\left(D=1\mathrel{\left| {D=1 C=1,\ B=0}\right. }C=1,\ B=0\right)\right)$
$=0.01+0.5\ \times 0.8\ \left(\ 0.1\times 0\ +\ 0.9\times 0.5\right)=0.19$
و در کل داریم :
$\mathrm{P(A=1|\ B=0,\ D=1)\ }\mathrm{=\ }\frac{\mathrm{P}\left(\mathrm{A=1},\mathrm{\ B=0,\ D=1}\right)\mathrm{\ }}{\mathrm{P}\left(\mathrm{\ B=0,\ D=1}\right)\mathrm{\ }}=\frac{0.01}{0.19}=\ \frac{1}{19}$
همانطور که در بالا میبینیم کمی حل سوال طولانی شد اما بسیاری از خطوط محاسبات در بالا را میتوان بصورت ذهنی سادهسازی کرد و نیازی به نوشتن دقیق تمام مراحل نیست و من در اینجا برای اینکه مراحل مشخص باشد و هیج ابهامی وجود نداشته باشد تمام بخشها را بصورت کامل نوشتم و در سر جلسه کنکور برای رسیدن به جواب باید تا حد امکان بصورت ذهنی سادهسازی کرد و بصورت خلاصه مراحل را نوشت.
$A+B\ge 3$
$B-C\le 0$
$B+D\ge 4$
$D-E-C\le 0$
$E+C\ge 2$
دروس تخصصی ۳ (مدار منطقی، معماری کامپیوتر و الکترونیک دیجیتال):
پاسخ تشریحی مدار منطقی کنکور ارشد کامپیوتر 1401
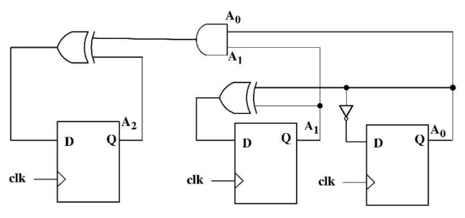
برای سادهتر شدن تحلیل مدار میتوانیم ابتدا تابع ورودی هر یک از فلیپفلاپها را با استفاده از مدار داده شده به دست آوریم:
$D_0=\bar{Q_0}$
$D_1=Q_0\oplus Q_1$
$D_2=(Q_0 Q_1)\oplus Q_2$
حال که توابع ورودی فیلپفلاپها را در اختیار داریم میتوانیم با یک مقدار A فرضی خروجی مدار پس از یک لبه فعال کلاک را به دست آوریم. برای این منظور ما $A=\overbrace{0}^{A_2}\overbrace{0}^{A_1}\overbrace{1}^{A_0}$فرض میکنیم. سپس با استفاده از توابع ورودی که در پیشتر به دست آورده بودیم، حالت بعدی مدار را پس از لبه فعال کلاک تحلیل میکنیم:
$D_0=\bar 1=0$
$D_1=1 \oplus 0=1$
$D_2= (0.1)\oplus 0=0$
بنابراین مقدار جدید A برابر است با 010 که برابر است با:$\underbrace{001}_{A}+1$
$module\; func\; (R,\; L,\; clk,\; Q);$
$input\; |0:2|R;$
$input\; L, clk;$
$output \;reg[0:2]Q;$
$always\; @ \;(posedge clk)$
$if\; (L)$
$Q \Longleftarrow R;$
$Else$
$Q \Longleftarrow \{Q[2],Q[0] $^$ Q[2],Q[1]\};$
$end \;module$
در ابتدای این قطعه کد متغیر 3 بیتی R و متغیرهای تک بیتی L,clk از نوع wire و به عنوان ورودی تعریف میشوند. پس از آن متغیر3 بیتی Q از نوع reg و به عنوان خروجی تعریف میشود. حال در حلقه always با هر لبه مثبت clk(کلاک) قطعه کد داخل این حلقه اجرا میشود. حال این بخش از کد را به صورت جداگانه بررسی میکنیم:اگر L=1 باشد مقدار R به صورت non-blocking به Q تخصیص داده میشود.
دبا کمی دقت متوجه میشویم اگر L=1 باشد، به نوعی عمل LOAD کردن ورودی شبیهسازی و انجام میشود. اما اگر L=0 باشد سیکل شمارش انجام خواهد شد. اگر مقدار اولیه را Q=000 فرض کنیم باز هم سیکلی نخواهیم داشت. بنابراین برای اینکه بتوانیم سیکل را بیابیم بایستی مقدار اولیه Q=001 فرض کنیم.
برای سادگی به دست آوردین سیکل میتوانیم $Q[2],Q[1]\}$^$Q\Leftarrow \{Q[2],Q[0]$ را به صورت زیر ترجمه کنیم:
$Q^*[0]=Q[2], Q^*[1]=Q[0]\oplus Q[2], Q^*[2]=Q[1]$
با این تفسیر سیکل مدار به صورت زیر خواهد بود:
$\underbrace{0}_{Q[0]}\underbrace{0}_{Q[1]}\underbrace{1}_{Q[2]}\to 110\to 011\to 111\to 101\to 100\to 010\to 001$
همانطور که ملاحظه میشود این مدار یک توالی شمارش با 7 سیکل دارد.
روش 1: رد گزینه
میدانیم که خروجی یک مدار به ازای مینترمهای آن برابر 1 است. حال با استفاده از همین نکته و چک کردن اختلاف بین گزینههای سوال میتوان گزینههای نادرست را رد کرد. بررسی گزینهها:
گزینه 1: مینترم $s_1s_0=10:10(\overbrace{1}^{A}\overbrace{0}^{B}\overbrace{1}^{C}\overbrace{0}^{D})$ بنابراین خط $I_2=\bar C=0$ انتخاب میشود. بنابراین $F=0$ و این گزینه رد میشود.
گزینه 3 و 4: مینترم $s_1s_0=11:15(\overbrace{1}^{A}\overbrace{1}^{B}\overbrace{1}^{C}\overbrace{1}^{D})$بنابراین خط $I_3=\bar {CD}=0$ انتخاب میشود. بنابراین $F=0$ و این گزینهها رد میشود.
با رد سه گزینه 1,3,4 پاسخ سوال ما گزینه دو خواهد بود.
روش دوم: جدول کارنو
برای سادگی میتوانیم ابتدا توابع خطهای ورودی را به دست آوریم:
$I_0=C, \;\;\; I_1=D, \;\;\; I_2=\bar C, \;\;\; I_3= \bar C \bar D $
جدول کارنو مدار مقابل را به صورت زیر خواهد بود:
جدول کارنو مدار مقابل را به صورت زیر خواهد بود:
$F(A,B,C,D)=\sum m(2.3.5.7.8.9.12)$
جدول حالت SR-Latch به صورت زیر است:
| $Q^*$ | $R$ | $S$ |
| $Q$ | $0$ | $0$ |
| $0$ | $1$ | $0$ |
| $1$ | $0$ | $1$ |
| غیرمجاز | $1$ | $1$ |
میدانیم T-Latch به ازای T=0 مقدار فعلی خودش را حفظ کرده و به ازای T=1 مقدار فعلی خود را قرینه میکند. توجه کنید که در همهی گزینهها خطی که از سمت چپ مدار خارج شده است همان ورودی T مدنظر ما است. حال میتوانیم با استفاده از توضیحات داده شده گزینهها را بررسی کنیم:
گزینه 1: اگر مقدار فعلی SR-Latch برابر 0 بوده و T=1 باشد. انتظار ما حالت بعدی 1 خواهد بود در حالی که با این انتسابها S=1 و R=1 میشود، که حالت غیرمجاز SR-Latch بوده و نباید به عنوان ورودی به آن داده شود. بنابراین این گزینه نادرست است.
گزینه 3: اگر مقدار فعلی SR-Latch برابر 0 بوده و T=1 باشد. انتظار ما حالت بعدی 1 خواهد بود در حالی که با این انتسابها S=0 و R=1 میشود، و در نتیجه آن SR-Latch ریست شده و مقدار 0 میگیرد. بنابراین این گزینه نادرست است.
گزینه 4: اگر مقدار فعلی SR-Latch برابر 0 بوده و T=1 باشد. انتظار ما حالت بعدی 1 خواهد بود در حالی که با این انتسابها S=0 و R=0 میشود، و در نتیجه آن SR-Latch مقدار قبلی خود یعنی 0 را حفظ میکند. بنابراین این گزینه نادرست است.
گزینه 2: جدول زیر حالات مختلف قابل تصور را برای این گزینه بیان میکند:
| T-Latch | $R = \overline{\overline{T} + \overline{Q}}$ | $S = \overline{\overline{T} + \overline{\overline{Q}}}$ | T | SR-Latch |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
پس گزینه دو پاسخ سوال ما خواهد بود.
$F(a,b,c,d)=(a.b.(c+\bar {b.d})+\bar {a.b}).(\bar {c+d})$
سادهسازی را میتوان با استفاده از خواص دمورگان و شرکتپذیری از طریق مراحل زیر انجام داد:
\[F(a,b,c,d) = \left( \text {a.b.}\left( c + \overline{b} + \overline{d} \right) + \overline{a} + \overline{b} \right).\left( \overline{c}.\overline{d} \right) = \left( abc + \underset{0}{\overset{\text{ab}\overline{b}}{︸}} + ab\overline{d} + \overline{a} + \overline{b} \right).\left( \overline{c}.\overline{d} \right) = abc\overline{c}d + ab\overline{c}\overline{d} + \overline{a}\overline{c}\overline{d} + \overline{b}\overline{c}\overline{d} = ab\overline{c}\overline{d} + \left( \overline{a} + \overline{b} \right)\overline{c}\overline{d} = \left( \underset{1}{\overset{\underset{x}{\overset{\text{ab}}{︸}} + \underset{\overline{x}}{\overset{\left( \overline{a} + \overline{b} \right)}{︸}}}{︸}} \right).\overline{c}\overline{d} = \overline{c}\overline{d}\]
مدار داده شده در این سوال یک مدار سنکرون است. برای سادگی تحلیل میتوانیم ابتدا توابع ورودی دو فلیپفلاپ را بدست آوریم:
$D_1=x.(Q_1+\bar Q_2)\;\;\;\;D_2=x.\bar Q_1.\bar Q_2$
حال به ازای حالت شروع 00 و رشته x=1110 حالات مدار را به دست میآوریم:
$00{\overset{x=1}{\to }}{11}{\overset{x=1}{\to }}{10}{\overset{x=1}{\to }}{10}{\overset{x=1}{\to }}00$
ابتدا جدول کارنو تابع را به دست میآوریم:
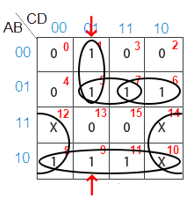
میدانیم هازارد در جدول کارنو به یکهایی اطلاق میشود که مجاورند و در یک دسته قرار ندارند. در جدول کارنو هازارد با فلش قرمز مشخص شده است. و به صورت $abcd=0001\leftrightarrow abcd=0110$ نمایش داده میشود.
پاسخ تشریحی معماری کامپیوتر کنکور ارشد کامپیوتر 1401
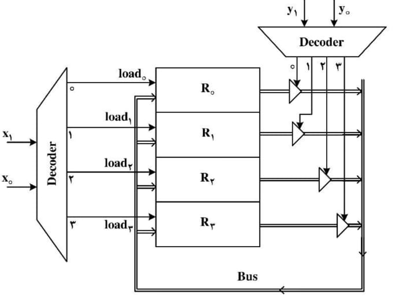
برای انتقال محتوای ثبات $R_1$ به $R_2$ باید محتوای $R_1$ روی باس مشترک قرار بگیرد برای این کار لازم است تا پایه شماره 1 دیکودر سمت راست فعال باشد تا بافر، Enable شود و محتوای $R_1$ را از خود عبور دهد. بنابراین پایههای $y_1y_0$ باید $ 0 1 $ باشند. (البته بهتر بود ارزش هر یک از پایههای دیکودر بیان شود ما در اینجا $y_0$ را بیت کم ارزش و $y_1$ را بیت پرارزش در نظر میگیریم. اگر این ارزشها را برعکس در نظر بگیریم به جواب گزینهی 2 خواهیم رسید.)
بعد از قرارگیری محتوای $R_1$ روی باس، نیاز است پایهی $Load3$ مربوط به $R_3$ فعال شود تا مقدار روی باس درون آن Load شود پس باید پایه شماره 3 دیکودر سمت چپ فعال باشد. بنابر این پایههای $x_1x_0$ هم باید $11$ باشند. پس جواب به صورت زیر در میآید:
\[\begin{matrix} x_1\ \ \ x_0\ \ \ y_1\ \ \ y_0 \\ 1\ \ \ \ 1\ \ \ \ 0\ \ \ \ 1\ \ \ \\ \end{matrix} = (D)_{\text{16}}\]
| $F$ | $c_0$ | $S_0$ | $S_1$ |
| $A$ | $0$ | $0$ | $0$ |
| $A+1$ | $1$ | $0$ | $0$ |
| $A+B$ | $0$ | $1$ | $0$ |
| $A+B+1$ | $1$ | $1$ | $0$ |
| $A-1$ | $0$ | $0$ | $1$ |
| $A$ | $1$ | $0$ | $1$ |
| $A-B-1$ | $0$ | $1$ | $1$ |
| $A-B$ | $1$ | $1$ | $1$ |
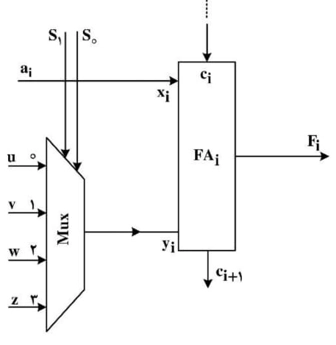
| U | V | W | Z | |
| 1 | $O$ | $B_i$ | $1$ | $B_i$ |
| 2 | $B_i$ | $1$ | $B_i$ | $O$ |
| 3 | $O$ | $B_i$ | $1$ | $B_i$ |
| 4 | $B_i$ | $O$ | $B_i$ | $1$ |
با توجه به جدول، وقتی پایههای $S_1S_0C_0$ به $000$ ست می شوند واحد F باید مقدار A را به خروجی منتقل کند. در این حالت پایهی u از مالتی پلکسر به خروجی منتقل میشود و مقدار آن هرچه باشد با تک تک بیتهای A جمع شده و به خروجی میرود پس واضح است برای این که مقدار A را بدون تغییر در خروجی داشته باشیم مقدار پایهی u باید 0 باشد (گزینههای 2 و 4 را رد میکنیم)
وقتی پایههای $S_1S_0C_0$ به $010$ ست شود واحد F باید جمع A و B را به خروجی منتقل کند در این حالت پایهی V از مالکتی پلکسر به خروجی منتقل میشود و مقدار آن با تک تک بیتهای A جمع خواهد شد پس اگر مقدار B را روی پایهی V قرار دهیم در نهایت $A+B$ را در خروجی خواهیم داشت پس با این حال گزینهی 3 نیز رد خواهد شد و گزینه 1 جواب است.
بررسی بیشتر: وقتی پایههای $S_1S_0C_0$ به $100$ ست شوند مقدار $A-1$ باید در خروجی ظاهر شود یکی از راههای پیادهسازی $A-1$ این است که تک تک بیتهای A را با 1 جمع کرده و از Carry تولید شده در مرحلهی آخر صرف نظر کنیم. پس اگر روی پایهی w مقدار ثابت 1 را قرار دهیم، 1 با تک تک بیتهای A جمع شده و خروجی مورد نظر را خواهیم داشت.
وقتی پایههای $S_1S_0C_0$ به $110$ ست شوند مقدار $A-B-1$ باید در خروجی ظاهر شود در این حالت پایهی z از مالتی پلکسر عبور میکند
\[A - B - \text{1}\ = A + \overline{B} + \text{1}\ - \text{1}\ = A + \overline{B}\]
همان طور که مشخص است باید تک تک بیتهای $A$ با تک تک بیتهای $\overline{B}$ جمع شوند تا طبق معادلهی بالا $A-B-1$ در خروجی ظاهر شود پس مقدار $\overline{B}$ باید روی پایهی $z$ قرار بگیرد.

فلگ carry در صورتی 1 میشود که از سمت چپترین بیت، رقم نقلی خارج شود با توجه به جمع انجام شده این فلگ 1 میباشد.
اولین بیت سمت چپ، بیت Sign است که مقدار آن برابر 1 میباشد ( دقت کنید پردازنده 16 بیتی است و carry تولید شده در آخرین مرحله دور انداخته میشود.)
یکی از راههای تشخیص سرریز در سیستم مکمل 2 مقایسهی رقم نقلی خارج شده از سمت چپترین بیت، با رقم نقلی وارد شده به سمت چپترین بیت میباشد ( در جمع بالا با دایره مشخص شدهاند) اگر این دو با هم برابر باشند سرریزی نخواهیم داشت و اگر با هم برابر نباشند سر ریز داریم. با توجه به جمع انجام شده سرریز نداریم و $O=0$ میباشد.
\[C_{n} \neq C_{n - \text{1}} \leftrightarrow Overflow = 1\ \ \Rightarrow Overflow = C_{n}\bigoplus C_{n - \text{1}}\]
(میدانید که XOR تابعی فرد است. XOR دو بیت در صورتی 1 میشود که یکی از آنها 1 و دیگری 0 باشد)
ما به دنبال %20 کارایی بیشتر هستیم. اگر کارایی در حالت اول را با $E_A$ نشان دهیم، کارایی در حالت دوم برابر است با:. $E_{B} = E_{A} + 0/2E_{A} = 1/2E_{A}$
پس سرعت اجرای برنامه در حالت دوم، 1/2 برابر سرعت اجرای برنامه در حالت اول است. به بیان دیگر زمان اجرای برنامه در حالت اول، 1/2 برابر زمان اجرای برنامه در حالت دوم است.
\[f_{A} = \text{1}G\ Hz \rightarrow T = \frac{\text{1}}{\text{10}^{\text{9}}}S = \text{1}\text{ns}\]
\[f_{B} = 1/5G\ Hz \rightarrow T = \frac{\text{1}}{{1/5\text{×}\text{10}}^{\text{9}}}S = \frac{\text{2}}{\text{3}}\text{ns}\]
\[\frac{A\text{زمان اجرای برنامه در حالت}\ }{B\text{زمان اجرای برنامه در حالت}} = \frac{n \times CPI_{A} \times T_{A}}{n \times CPI_{B} \times T_{B}} = \frac{n \times 1\ \times 1\ }{n \times CPI_{B} \times \frac{\text{2}}{\text{3}}} = 1/2\]
\[\Rightarrow \text{CP}I_{B} = \frac{\text{1}}{1/2 \times \frac{\text{2}}{\text{3}}} = \frac{\text{1}}{0/8} = 1/25\]
$= log\frac{\text{حجم حافظه اصلی}}{\text{حجم کش}\ } + \log K$ تعداد بیتهای tag در نگاشت K-way Set Associative
Cpu آدرسهای 24 بیتی تولید میکند یعنی حجم حافظه اصلی $2^{24}$ واحد آدرس پذیر است. با توجه به این که واحد آدرس پذیر در سئوال مشخص نشده، اگر واحد آدرس پذیر را بایت در نظر بگیریم، حل مسئله به شرح زیر است:
\[\log{\frac{\text{2}^{\text{24}}\text{Byte}}{\text{2}^{\text{20}}\text{Byte}} + \log{K = \text{10}\ \ \Rightarrow \log K = \ \text{6} \rightarrow K = \text{64}}}\]
اگر کش $64- way $ باشد یعنی در هر ست 64 بلاک قرار دارد و هر بلاک 8 بایت است.
حجم کش نیز $2^{20}$ بایت است با توجه به این اطلاعات تعداد set ها را به دست میآوریم.
تعداد ست های کش $\text{2}^{\text{6}} \times \text{2}^{\text{3}} = \text{2}^{\text{9}}\;\;\;.\;\;\;\frac{\text{2}^{\text{20}}}{\text{2}^{\text{9}}} = \text{2}^{\text{11}} \leftarrow$
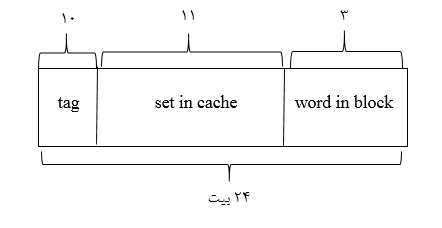
$LD\;X1,20(X10)$
$LD\;X2,30(X20)$
$AAD\;X3,X2,X1$
به این مد آدرسدهی Base Indirect گفته میشود. در واقع دستورات به صورت زیر در میآیند:
محتوای آن آدرسی از حافظه را که در خانهی $x_{10}+20$ ذخیره شده است را درون $x_1$ قرار بده $I_{\text{1}}:LD\ \ X_{\text{1}},\ \left\lbrack X_{\text{10}} + \text{20}\ \right\rbrack \rightarrow$
$I_{\text{2}}:LD\ \ X_{\text{2}}\ ,\ \left\lbrack X_{\text{20}} + \ \text{30} \right\rbrack$
$I_{\text{3}}:ADD\ \ X_{\text{3}}\ ,X_{\text{2}},X_{\text{1}}$
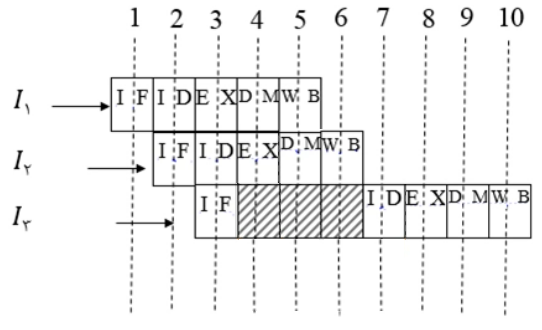
$I_1$ و $I_2$ دستورات حافظهایی هستند و محتوای آن خانه از حافظه که آدرس آن در $x_{10}+20$ یا $x_{20}+30$ در قرار گرفته را درون خانههای $X_1$ و $X_2$ ، Load میکنند.
با توجه به پایپ لاین بالا، هیچ دو مرحلهایی هم زمان دسترسی به حافظه ندارند چون با توجه به صورت سئوال در صورت رخداد این مخاطره، مخاطره را با اضافه کردن تأخیر، رفع کردیم.
* در این مرحله $I_1$ مشغول نوشتن در خانهی $X_1$ از حافظه میباشد بنابراین دستور $I_2$ نمیتواند دسترسی به حافظه داشته باشد پس با اضافه کردن یک تأخیر در این مرحله، مخاطره را رفع کردهایم
* نکتهی دیگری که وجود دارد این است که اجرای $I_3$ باید بعد از اجرای کامل $I_2$ و $I_1$ صورت بگیرد زیرا $I_3$ میخواهد محتوای خانههای $X_2$ و $X_3$ را با هم جمع کند اگر مرحلهی EX زودتر از پایان یافتن دستورات $I_2$ و $I_1$ انجام شود، مقادیر نادرستی با هم جمع و در نهایت در $X_1$ قرار میگیرد. تأخیرهایی که با ستاره مشخص شدهاند به همین منظور میباشند.
با توجه به خطچینهایی که در شکل مشخص شده مشاهده میکنیم که انجام این 3 دستور در 10 پالس ساعت انجام میشود.
با توجه به این که شیوه نمایش اعداد به صورت هنجار شده است بزرگترین عدد مثبت قابل نمایش در این سیستم، قالب روبرو را دارد: $1/1\text{…}\text{1} \times \text{2}^{E}$
بیشترین مقداری که E میتواند داشته باشد این است که همهی بیتهای مربوط به Exponent را برابر با 1 قرار دهیم با توجه به این که برای نمایش نما در این سیستم از روش $ Biased – 16$ استفاده میشود و 5 بیت برای نمایش نما داریم پس بیشترین مقدار E برابر است با $E + bias = \text{31}\ \ \Rightarrow E = \text{15}$
پس بزرگترین عدد به این صورت خواهد شد: $1/1\text{…}\text{1} \times \text{2}^{15}$
برای نمایش مانتیس از روش Explicit – One استفاده شده است یعنی 1 سمت چپ ممیز نیز باید در ثبات ذخیره شود و به صورت ضمنی وجود ندارد. فضای مانتیس 10 بیت است پس بنابراین بزرگترین عدد به شکل زیر خواهد شد:
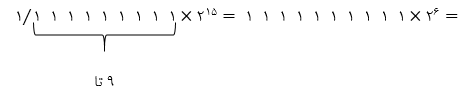
\[\left( \text{2}^{\text{10}} - \ \text{1} \right) \times \text{2}^{\text{6}} = \text{2}^{\text{16}} - \text{2}^{\text{6}}\]
پاسخ تشریحی الکترونیک دیجیتال کنکور ارشد کامپیوتر 1401
$P_{Total}=P_{Dynamic}=\alpha CV_{DD}^2f_{CLK} \le 10\mu W\Rightarrow 0.1\times C\times 4\times500MHz\le 10\mu W$
$C\le 5\times 10^{-14}\Rightarrow C\le 50\times 10^{-15}\equiv50ff$
| F | Z | Y | X |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
چون حداقل تعداد گیت خواسته شده ، ابتدا جدول کارنو را رسم کرده و تابع خروجی را بدست میآوریم. سپس شکل مدار را رسم کرده و تعداد ترانزیستورهای به کار رفته را میشماریم:
\[F\ = \ \overline {y}\ + \ xz\]
حال با توجه به تابع بدست آمده، شبکه بالابر مدار CMOS گفته شده را رسم میکنیم:
از شکل بالا مشخص است که ما نیاز به 3 ترانزیستور PMOS در شبکه بالابر و 3 ترانزیستور NMOS در شبکه پایینبر داریم. همچنین چون دو متغیر در شکل بالا NOT شدهاند، نیاز به دو معکوس کننده CMOS که شامل 4 ترانزیستور هستند نیز داریم.
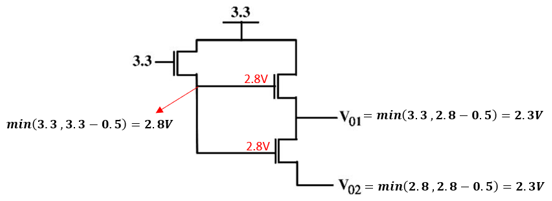
مدار داده شده را به ازای ورودیهایی تست میکنیم که خروجی را به زمین متصل کنند. (خروجی را صفر کنند) اگر هر کدام از a یا b برابر صفر شود، خروجی به زمین متصل میشود اما ولتاژ آن برابر 0 نمیشود زیرا ترانزیستور PMOS صفر را کامل از خود عبور نمیدهد در نتیجه ولتاژ خروجی در این حالت برابر $|V_{tp}$ خواهد شد.
حال اگر هر دو پایه a و b برابر 1 شوند، ترانزیستورهای طبقه پایینبر خاموش بوده و شبکه بالابر فعال و ورودی را به منبع متصل میکند اما در این حالت ولتاژ خروجی برابر $V_{dd}$ نمیشود زیرا ترانزیستور NMOS یک را کامل از خود عبور نمیدهد در نتیجه ولتاژ خروجی در این حالت برابر$V_{dd}-2V_{tn}$ خواهد شد.
حال برای حالتهای دیگر ورودی نیز باید خروجی را چک کنیم که آیا در آن حالات مدار صحیح کار میکند یا خیر. برای اینکار از جدول صحت استفاده میکنیم:
| Out | b | a |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
با توجه به جدول صحت متوجه میشویم که عملکرد این مدار مشکلی نداشته و نشان دهنده منطق AND است (رد گزینه 1) در نتیجه این مدار یک مدار AND است با این تفاوت که صفر و یک را کامل از خود عبور نمیدهد.
توان مصرفی CMOS ANDبرابر صفر بود زیرا 0 و 1 منطقی را کامل از خود عبور میداد اما چون این مدار صفر و یک را کامل از خود عبور نمیدهد در نتیجه توان مصرفی آن صفر نیست.(گزینه 4 میتواند درست باشد)
میدانیم که تاخیر مدار CMOS AND در حالت خروجی 1 برابر $t_{PLH}=0.69\tau _{charge}=0.69R_PC_L$است و همچنین در حالت خروجی 0 برابر $t_{PLH}=0.69\tau _{discharge}=0.69R_nC_L$است. اما با توجه به اینکه در حالت خروجی 1 در مدار این سوال میزان تاخیر کمتر و در حالت خروجی 0 میزان تاخیر بیشتر شده، نمیتوان درباره میزان تغییر کل تاخیر صحبت کرد. (رد گزینه 2)
در صورت سوال مقدار $V_{OL}$ داده شده در نتیجه میتوان نوشت:
\[\underset {2.8}{\overset{\underset{3.3}{\overset{V_{\text{GS}}}{︸}}\ - \ \underset{0.5}{\overset{V_{\text{tn}}}{︸}}}{︸}}\ \boxed{?}\ \underset{0.5}{\overset{V_{\text{DS}}}{︸}}\ \longrightarrow \ V_{\text{GS}}\ - \ V_{\text{tn}}\ \gg \ V_{\text{DS}}\]
در نتیجه ترانزیستور در ناحیه خطی قرار دارد:
\[I = \frac {3.3\ - \ 0.5}{100K\Omega} = {K^{'}}_{n}\left( \frac{W}{L} \right)_{n}\left( V_{\text{DS}}\left( V_{\text{GS}} - V_{\text{tn}} \right) \right)\]
\[I = \frac {2.8}{100K\Omega} = 10\mu\left( \frac{W}{L} \right)_{n}\left( 0.5(3.3 - 0.5) \right) = 10\mu\left( \frac{W}{L} \right)_{n} \times 0.5 \times 2.8 \longrightarrow \ \left( \frac{W}{L} \right)_{n}= 2\]
بررسی گزینه 1: پدیده مدولاسیون طول کانال باعث افزایش جریان درین-سورس در زمان روشن بودن ترانزیستورها میشود.
بررسی گزینه 2: توان مصرفی پویا در این فناوری با خازن بار نسبت مستقیم و با فرکانس کلاک نسبت مستقیم دارد.
بررسی گزینه 4: افزایش ولتاژ تغذیه تاثیری روی تاخیر گیت(دروازه) ندارد بلکه تاخیر به میزان مقاومت از منبع تا خروجی (یا از زمین تا خروجی) و خازن خروجی بستگی دارد.
دروس تخصصی ۴ (سیستمهای عامل، شبکههای کامپیوتری و پایگاه دادهها):
پاسخ تشریحی سیستم عامل کنکور ارشد کامپیوتر 1401
بنابر اطلاعات داده شده در صورت سوال نرخ انتقال اطلاعات بین حافظه اصلی و حافظه مجازی 50 MB / Sec است. با توجه به اینکه اندازه هر فرآیند 10MB است. بنابراین انتقال هر فرآیند بین حافظه اصلی و حافظه مجازی به $\frac{10}{50}=200 msec$زمان نیاز دارد. حال باتوجه به اینکه cpu time هر فرآیند نیز $200 msec $ است و بنابه فرض سوال فرآیندها امکان اجرای همزمان با DMA را دارند. بنابراین زمانی که یک فرآیند در حال سپری کردن زمان پردازش خودش است، DMA فرآیند دیگری را از حافظه مجازی به اصلی انتقال داده و از آنجایی که این زمان انتقال با زمان CPU فرآیند در حال اجرا برابر است، CPU به محض اتمام یک فرآیند، فرآیند دیگری برای اجرا در حافظه اصلی خواهد داشت. که در این صورت CPU هیچگاه در صورت وجود فرآیندی برای اجرا بیکار نمانده. بنابراین بهرهوری آن 100% خواهد بود.
| P3 | P2 | P1 | |
| مدت زمان CPU | 10 | 20 | 5 |
| دوره تناوب | 40 | 50 | 25 |
الگوریتم زمانبندی مطرح شده در این سوال یک الگوریتم قبضهای اولویتدار است که اولویت آن را میتوان به صورت $\uparrow \text{اولویت} = \downarrow \frac{cpu \ \text{مدت} \ \text{زمان} }{\text{دوره} \ \text{تناوب}}$ بیان کرد. بنابراین اولویت هر یک از سه فرآیند P1,P2,P3 برابر خواهد بود با:
$P_1=\frac {5}{25}=\frac {20}{100} $ اولویت : 1
$P_3=\frac {10}{40}=\frac {25}{100} $ اولویت : 2
$P_2=\frac {20}{50}=\frac {40}{100} $ اولویت : 3
زمانهای مختلف ورود هر کدام از فرآیندها بر اساس دوره تناوبشان نیز به صورت زیر خواهد بود:
$P_1:0\rightarrow 25\rightarrow 50\rightarrow 75\rightarrow 100\rightarrow 125\rightarrow 150\rightarrow 175\rightarrow 200$
$P_2:0\rightarrow 50\rightarrow 100\rightarrow 150\rightarrow 200$
$P_3:0\rightarrow 40\rightarrow 80\rightarrow 120\rightarrow 160\rightarrow 200$
حال که اولویت هرکدام از فرآیندها و زمانهای ورود را داریم نمودار گانت را برای این سه فرآیند رسم میکنیم: (لطفا نمودار عکس زیر رسم شود)
میدانیم بهرهوری CPU برابر است با:$\frac { \text{بیکار نبوده cpu زمان هایی که}}{\text{کل زمان}}$
بنابراین بهرهوری CPU در این سوال برابر خواهد بود با:$\frac{170}{200}=0.85$
بررسی شرط انحصار متقابل: با توجه به اینکه ظرفیت آسانسور 1 نفر است. بنابراین زمانی که آسانسور پر باشد، فرد دیگری نمیتواند وارد آن شود. و همچنین از آنجایی که در هر طبقه فقط 1 نفر زندگی میکند، امکان اینکه دو نفر بخواهند در یک لحظه وارد آسانسور شوند نیز وجود ندارد. بنابراین شرط انحصار متقابل برقرار است.
بررسی شرط انتظار محدود: در بدترین حالت مطابق مثال بیان شده در متن سوال اگر آسانسور در کلیه طبقات 5 تا 19 توقف داشته باشد و هر شخص فقط یک طبقه با این آسانسور به بالا حرکت کند و شخصی در طبقه همکف منتظر آسانسور باشد. آسانسور نهایتا با رسیدن به طبقه 19 حرکت خود را به سمت پایین آغاز میکند. و بنابه فرض سوال تا زمانی که به طبقه همکف نرسد به حرکت خود به سمت پایین ادامه میدهد. بنابراین پس از مدت زمان محدودی آسانسور به طبقه همکف خواهد رسید. بنابراین شرط انتظار محدود برقرار است.
بررسی شرط پیشرفت: فرض کنید آسانسور در حال حمل شخصی از طبقه 1 به 3 باشد. در همین حال شخصی در طبقه همکف درخواست آسانسور میدهد. و تا زمانی که آسانسور به طبقه این شخص نرسد هیچکس درخواست آسانسور نداشته باشد. تحت این شرایط پس از آنکه آسانسور در طبقه 3 خالی شود. بایستی تا طبقه 19 به حرکت خود ادامه بدهد در حالی که هیچکدام از ساکنان طبقات 3 الی 19 درخواست آسانسور را نکردهاند. بنابراین این اشخاص در حالی که خارج از ناحیه بحرانی هستند و قصد ورود به آن را نیز ندارند مانع ورود مسافر ساکن در طبقه همکف به آسانسور هستند. بنابراین این مسئله شرط پیشرفت را نقض میکند.
میدانیم متوسط زمان دسترسی از دو بخش تشکیل شده و برابر است با:
زمان خواندن داده + زمان ترجمه آدرس = متوسط زمان دسترسی
بنابراین در این سوال متوسط زمان دسترسی برابر خواهد بود با:
$ \; 0.02\times (150\times \overbrace{2}^{\text{صفحه بندی 2 سطحی}}) + 150=156 $ = متوسط زمان دسترسی
| $R_2$ | $R_1$ | Allocation |
| 2 | 1 | $P_1$ |
| 5 | 2 | $P_2$ |
| 0 | 2 | $P_3$ |
| 1 | 1 | $P_4$ |
| 0 | 0 | $P_5$ |
| $R_2$ | $R_1$ | MAX |
| 2 | 5 | $P_1$ |
| 9 | 3 | $P_2$ |
| 5 | 4 | $P_3$ |
| 4 | 1 | $P_4$ |
| 5 | 8 | $P_5$ |
| Available | ||
| $R_2$ | $R_1$ | |
| y | x | |
حالت امن به حالت گفته میشود که حداقل یه ترتیب برای تخصیص منابع به فرآیندها وجود داشته باشد به نحوی که تمامی فرآیندها امکان اجرا را داشته باشند و در حین این تخصیص به بنبست نرسیم. در گام نخست برای حل این سوال، جدول Needed را از تفاضل خانه به خانه جدول Allocation از جدول MAX بدست میآوریم:
| $R_2$ | $R_1$ | Needed |
| 0 | 4 | $P_1$ |
| 4 | 1 | $P_2$ |
| 5 | 2 | $P_3$ |
| 3 | 0 | $P_4$ |
| 5 | 8 | $P_5$ |
سوال از ما حداقل مقدار x+y را خواسته که برای بدست آوردن آن میتوانیم گزینهها را به ترتیب صعودی مقدارهایشان بررسی کنیم:
گزینه 4: اگر x+y=4 باشد دو حالت زیر با توجه به جدول Needed برای جدول Available وجود خواهد داشت که در همان ابتدا دچار بنبست نباشد:
| $R_2$ | $R_1$ | حالت |
| 3 | 1 | 1 |
| 0 | 4 | 2 |
حالت 1: با این حالت میتوانیم توالی $P_4\rightarrow P_2\rightarrow P_3\rightarrow P_1$ را به دست آوریم که پس از اجرای $R_2=P_1$ $R_1=6 و 12$خواهد شد. در این شرایط به علت اینکه برای اجرای آخرین فرآیند یعنی $P_5$ نیاز به 8 واحد از منبع$R_1$داریم، به بنبست میرسیم. سایر ترتیبهای اجرا نیز در این حالت همین نتیجه را در برخواهند داشت.
حالت 2: در این حالت پس از اجرای $R_2=2,P_1$ و $R_1=5$ خواهد شد. که در همین نقطه متوقف میشویم.
بنابراین حالت امنی به ازای x+y=4 وجود نخواهد داشت.
گزینه 3: اگر x+y=5 باشد و جدول Available را به صورت زیر فرض کنیم:
| $R_2$ | $R_1$ |
| 1 | 4 |
ترتیب تخصیص $P_1\rightarrow P_4\rightarrow P_2\rightarrow P_5$ یک حالت امن به ما میدهد. بنابراین این گزینه حداقل مقدار بوده و نیازی به بررسی دو گزینه دیگر نیست.
میدانیم که مدیریت فرآیندها ، زمانبندی پردازنده و مدیریت I/O از وظایف سیستمعامل است. که این موارد میتوانند تاثیر مستقیم در بهرهوری CPU داشته باشند.بنابراین گزینه 3 و 4 پاسخ سوال ما نخواهند بود. گزینه 1 نیز نادرست است زیرا بنابر الگورتیم فوننیومن اگر CPU برنامهای برابر اجرا نداشته باشد به وضعیت Halt خواهد رفت و فقط شامل اجرای فرآیندها نخواهد بود، که این مورد در گزینه 1 بیان نشده و ناقص است. همچنین امکان اتلاف زمان CPU به سبب I/O وجود دارد. بنابراین ممکن است بهرهوری CPU تحت شرایطی کمتر از 100 درصد نیز باشد. گزینه 2 بیان بهتر و کاملتری از الگوریتم فننیومن را دارد. بنابراین گزینه 2 در بین 4 گزینه مطرح شده در این سوال درستتر است.
فرآیند zombie: فرآیندی است که وظیفهاش را به طور کامل انجام داده است اما هنوز در جدول فرآیند یک entry دارد. فرآیندی که زامبی شده است امکان از بین بردن خودش را ندارد. بنابراین فرآیند پدر بایستی اجرا شده و دستور از بین بردن فرآیند فرزند zombie شده خود را صادر کند. در صورتی که فرآیند پدر این دستور را صادر نکند، فرآیند فرزند zombie شده باقی خواهد ماند.
فرآیند orphan: فرآیند فرزندی که والدش پس از اتمام کار و یا از بین رفتن منتظر اجرای فرآیند فرزند نمانده و فرآیند فرزند پس از آن همچنان در حال اجراست. بنابراین اگر فرآیند والد دستور wait را برای فرآیند فرزند zombie شده خود صادر نکند و خودش از بین برود، فرآیند zombie شده به orphan تبدیل میشود.
پاسخ تشریحی شبکه های کامپیوتری کنکور ارشد کامپیوتر 1401
| تکه 4 | تکه 3 | تکه 2 | تکه 1 | |
| 15MByte | 18MByte | 12MByte | 15MByte | MPD1 |
| 9MByte | 12MByte | 7.5MByte | 9MByte | MPD2 |
| 6MByte | 7.5MByte | 3MByte | 6MByte | MPD3 |
000
myport = 4321
destination = socket (AF_INET, SOCK_DGRAM)
destination.bind((”,80))
برنامه سروری که این کلاینت با آن وصل میشود، از چه شماره پورتی برای خود و چه شماره پورتی برای کلاینت استفاده میکند؟

AS5 - AS6 - AS4 - AS2- AS1 - 112.14.2.0
AS7 - AS5- AS6 - AS3 - AS1-112.14.2.0
AS5 - AS6 - AS3 - AS1-112.14.2.0
چنانچه سامانه خودگردان ۴ دست از اعمال سیاست بردارد و هیچ سیاستی را اعمال نکند، چه اطلاعات دیگری توسط iBGP به مسیریابیهای درون سامانه خودگردان ۸ خواهد رسید؟
VLAN1: 10.0.0.0 و VLAN2: 172.16.0.0 و VLAN3: 192.168.0.0
پاسخ تشریحی پایگاه داده کنکور ارشد کامپیوتر 1401
$(\delta(STUD))\cap (\delta(CRS))=?$
$Avg>16 \;\;\;unit=3$
((معدل)Avg ,(شهر)City , (نام و نامخانوادگی) sname , (شماره دانشجویی) S# )) STUD (دانشجو)
((مدرک) DEGREE ,(شماره اتاق) Office ,(نام استاد)Pname) PROF (استاد)
((تعداد واحد) Unit ,(نام درس) cname ,(کد درس) c#) CRS (درس)
((نمره) Score ,Pname ,(کد ترم)Term ,S# ,S# ,C# ,(کد) Sec#) SEC (اخذ درس)
| جدول دانشجو | (Student) |
| نام و نامخانوادگی | شماره دانشجویی |
| Name | Stn |
| جدول درس | (Course) |
| نام درس | کد درس |
| CName | Code |
|
جدول درس اخذ شده |
(Taken) | |
| کد درس | شماره دانشجو | نمره |
| CCode | SStn | Mark |
select Name
from Student S
where not exists ((select *
from Taken T join Student on Stn = SStn
where Name = 'Mina Asadi' and
not exists
( select *
from Taken B
where B.SStn = S.SSn
and T. CCode = B.CCode))
$R(X,Y,Z,S,T,U, W)$
$ F = {S , X, T Y,X , Y, XY , TUZ}$